В любой электрической цепи в соответствии с первым законом Кирхгофа алгебраическая сумма токов, направленная к узлу равна нулю: .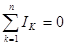

В соответствии со вторым законом Кирхгофа алгебраическая сумма э. д. с. 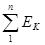в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений в этом контуре .

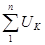При расчете электрических цепей методом применения зако­нов Кирхгофа выбирают условные положительные направления токов, ЭДС и напряжений на участках цепи, которые обозначают стрелками на схеме, затем выбирают замкнутые контуры и за­даются положительным направлением обхода контуров. При этом для удобства расчетов направление обхода для всех контуров рекомендуется выбирать одинаковым (например, по часовой стрелке).

При составлении уравнений по второму закону Кирхгофа для электрических цепей, содержащих источники тока, выбирают замкнутые контуры без источников тока. Для получения незави­симых уравнений необходимо, чтобы в каждый новый контур входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму зако­ну Кирхгофа.

Число уравнений, составленных по второму закону Кирхгофа, необходимое для выполнения расчета данной электрической цепи, равно числу неизвестных N.

В большинстве случаев параметры источников ЭДС или на­пряжения, источников тока, сопротивлений участков электри­ческой цепи известны, при этом число неизвестных равно раз­ности между числом ветвей и числом источников тока N=( N_B — N_T). Для упрощения расчетов сначала записывают более простые уравнения, составленные по первому закону Кирхгофа, а недостающие — по второму закону Кирхгофа.

Число уравнений, составленных по первому закону Кирхгофа, берется на единицу меньше числа узлов n_y в цепи: 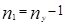. При этом токи, направленные к узлу, условно принимаются по­ложительными, а направленные от узла — отрицательными.

Остальное число уравнений 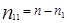, составляется по вто­рому закону Кирхгофа: 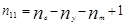, где n_в– число ветвей цепи; n_y– число узлов цепи; n_m– число источников тока цепи.

При составлении уравнений по второму закону Кирхгофа ЭДС источников принимаются положительными, если направле­ния их действия совпадают с выбранным направлением обхода контура, независимо от направления тока в них. При несовпаде­нии их записывают со знаком «—». Падения напряжений в вет­вях, в которых положительное направление тока совпадает с направлением обхода, независимо от направления ЭДС в этих ветвях — со знаком «+». При несовпадении с направлением об­хода падения напряжений записываются со знаком «—».

В результате решения полученной системы из n уравнений находят действительные направления определяемых величин с учетом их знака. При этом величины, имеющие отрицательный знак, в действительности имеют направление, противоположное условно принятому. Направления величин, имеющих положитель­ный знак, совпадают с условно принятым направлением.

Решение полученной системы уравнений позволяет определить неизвестные величины. При этом величины со знаком «+» в действительности имеют направление, совпадающее с соответствующим первоначально заданным на схе­ме условным направлением. Величины со знаком «—» в действи­тельности имеют направление, противоположное первоначально заданному условному направлению, показанному на схеме.

Метод контурных токов

Этот метод позволяет уменьшить ко­личество уравнений системы, составляемых по законам Кирхгофа, до

где n_в– число ветвей цепи;

n_y– число узлов цепи;

    n_m– число источников тока цепи.

Он основан на том, что ток в любой ветви цепи можно предста­вить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При использовании метода перед расчётом выбирают на­правления и путь протекания контурных токов - по любой ветви дол­жен протекать хотя бы один выбранный контурный ток. Общее число неизвестных контурных токов определяется величиной k (1). Причём, из пути их протекания следует исключить ветви с источниками тока.

Пример:

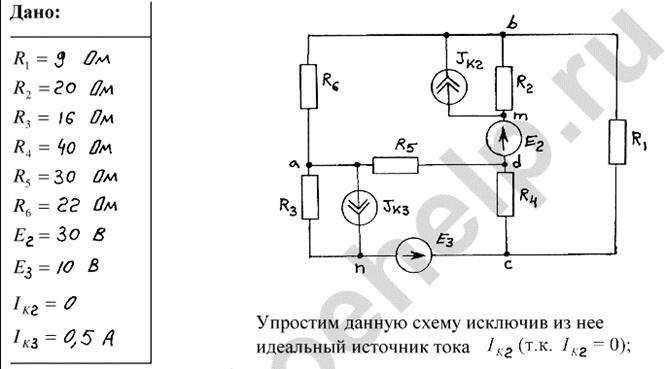
Исходные данные:

R₁ =24 Ом; R₂=70 Ом; R₃=44 Ом; R₄=12 Ом; R₅=20 Ом; R₆=30 Ом; Е₂=40 В; Е₃=19,6 В; J_K2=0 А; J_K3=0,1 А.

При расчёте этой схемы методом контурных токов возможны два пути:

1) Преобразование исходной схемы не производится.

2) Предусматривает преобразование реальных источников тока в эквивалентную э.д.с.

Для расчёта данной схемы выбираем второй путь и при этом учтём, что

J_K2=0 А. Преобразуем J_K3 в E₃^*. Пользуясь законом Ома, получаем E₃^*= J_K3R₃=4,4 B.

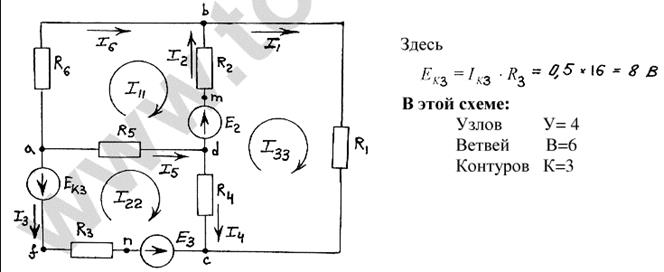
Схема, полученная после преобразования представлена на рисунке 2.

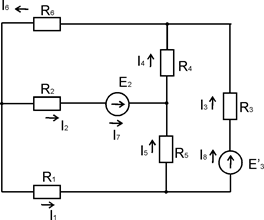
Рисунок 2 – Преобразованная схема

E₃^’=E₃+ E₃^*=19,6+4,4=24(B)

После упрощения исходной схемы можно непосредственно перейти к реализации метода контурных токов. Для этого нужно определить количество контурных токов. Сделать это можно по формуле:

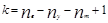
где n_в– число ветвей цепи;

n_y– число узлов цепи;

    n_m– число источников тока цепи.

В рассматриваемой схеме n_в=6, n_y=4; n_m=0.

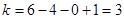
Итак, зная количество контурных токов, нужно выбрать их направления.

Схема с направлениями контурных токов представлена на рисунке 3.

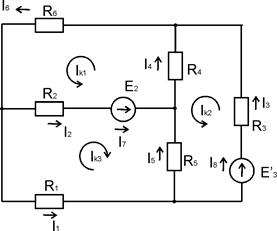
Рисунок 3 – Преобразованная схема с направлениями контурных токов

Составим систему уравнений по второму закону Кирхгофа для определения неизвестных контурных токов (порядок системы равен k):

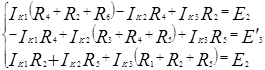
Составим матрицу:

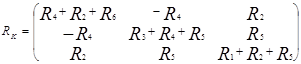
Отсюда выразим матрицу контурных токов:

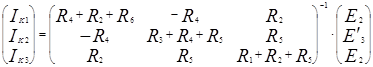
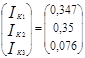
Зная значения контурных токов, можно найти реальные токи. Они будут равны комбинации контурных токов.

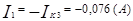
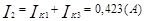
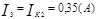
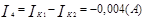
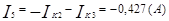
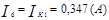
Используя контурные токи, мы получили токи конкретные.

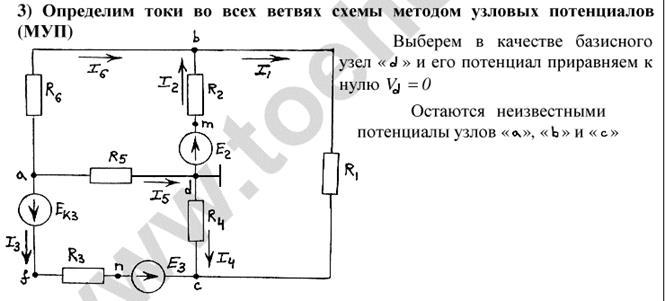
10) Метод узловых напряжений (потенциалов)