Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной 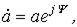
тригонометрической 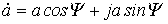 или
или
алгебраической 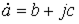 - формах.
- формах.
Например, ЭДС 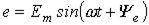 , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
, изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
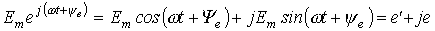 .
.
Фазовый угол 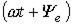 определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
 .
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
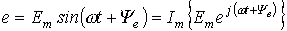 , ,
| (4) |
Комплексное число 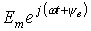 удобно представить в виде произведения двух комплексных чисел:
удобно представить в виде произведения двух комплексных чисел:
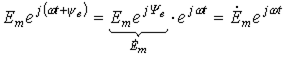 , ,
| (5) |
Параметр 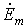 , соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:
, соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой: 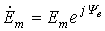 , а параметр
, а параметр 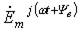 - комплексом мгновенного значения.
- комплексом мгновенного значения.
Параметр 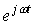 является оператором поворота вектора на угол w t относительно начального положения вектора.
является оператором поворота вектора на угол w t относительно начального положения вектора.
Вообще говоря, умножение вектора на оператор поворота 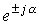 есть его поворот относительно первоначального положения на угол ±a.
есть его поворот относительно первоначального положения на угол ±a.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды 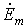 и оператора поворота
и оператора поворота 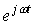 :
:
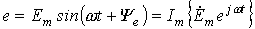 .
.
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
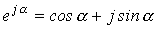 , ,
| (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
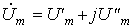 ,
,
- то для записи ее в показательной форме, необходимо найти начальную фазу 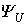 , т.е. угол, который образует вектор
, т.е. угол, который образует вектор 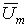 с положительной полуосью +1:
с положительной полуосью +1:
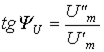 .
.
Тогда мгновенное значение напряжения:
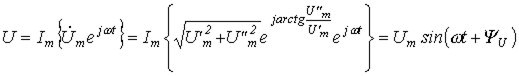 ,
,
где 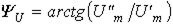 .
.
При записи выражения для определенности было принято, что 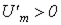 , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если
, т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если 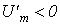 , то при
, то при 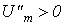 (второй квадрант)
(второй квадрант)
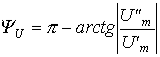 , ,
| (7) |
а при 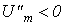 (третий квадрант)
(третий квадрант)
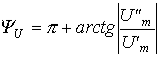
| (8) |
или
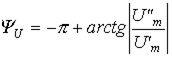
| (9) |
Если задано мгновенное значение тока в виде 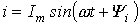 , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
, то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
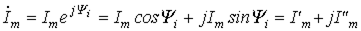 .
.
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока 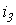 по рис. 5 получим:
по рис. 5 получим:
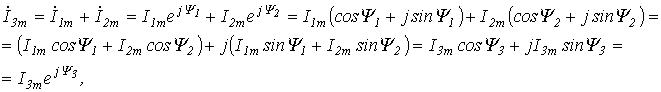
где 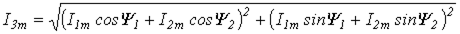 ;
;
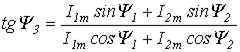 .
.
Дата: 2019-05-29, просмотров: 323.