Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Сопротивление- идеализированный элемент цепи, характеризующий потери энергии на нагрев, механическую работу или излучение электромагнитной энергии.

Закон Ома

 Сопротивление есть отношение напряжения на данном элементе цепи к току, проходящему через него. 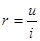.Основными законами теории це­пей наряду с законом Ома являют­ся законы баланса токов в развет­влениях (первый закон Кирхгофа) и баланса напряжений на замкну­тых участках цепи (второй закон Кирхгофа).

Распределение токов и напряже­ний в электрических цепях подчи­няется законам Кирхгофа.

Первый закон Кирхгофа

Алгебраическая сумма токов в узле равна нулю: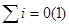

Суммирование распространяется на токи в ветвях, сходящихся в рассматриваемом узле. При этом знаки токов берутся с учетом выбранных положительных направлений токов: всем токам, направленным от узла, в уравнении (1) приписывается одинаковый знак, например поло­жительный, и соответственно все токи, направленные к узлу, входят в уравнение (1) с противополож­ным знаком.

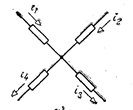На рис. в качестве при­мера показан узел, в котором сходятся четыре ветви. Уравнение (1) имеет в этом случае вид:— i₁ — i₂+ i₃+ i₄=0.

Первый закон Кирхгофа выра­жает тот факт, что в узле электри­ческий заряд не накапливается и не расходуется.Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.

Первый закон Кирхгофа приме­ним не только к узлу, но и к любо­му контуру или замкнутой поверх­ности, охватывающей часть элек­трической цепи, так как ни в каком элементе цепи, ни в каком режиме электричество одного знака не мо­жет накапливаться.

Так, например, для схемы

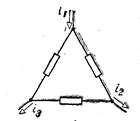имеем: — i₁+ i₂+ i₃=0.

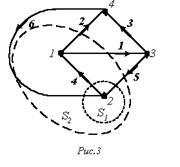
Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение

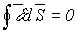
(1)

где 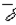- вектор плотности тока; 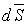- нормаль к участку dS замкнутой поверхности S.

Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S₂ графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать

.

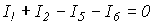Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:

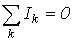
(2)

т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.

При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.

Введем столбцовую матрицу токов ветвей

I=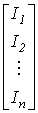

Тогда первый закон Кирхгофа в матричной форме записи имеет вид:

АI=O

(3)

– где O - нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не А_Н, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.

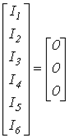
В качестве примера запишем для схемы на рис. 3

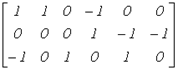
Отсюда для первого узла получаем

,

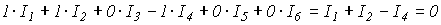что и должно иметь место.

Второй закон Кирхгофа

Алгебраическая сумма э.д.с. в любом контуре цепи равна алге­браической сумме падений напря­жения на элементах этого контура: .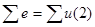

Обход контура совершается в произвольно выбранном направ­лении, например по ходу часовой стрелки. При этом соблюдается сле­дующее правило знаков для э.д.с. и падений напряжения, входящих в (2): э.д.с. и падения напряже­ния, совпадающие по направлению с направлением обхода, берутся с одинаковыми знаками.

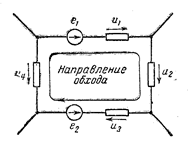Например, для данной схемы 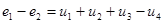.Уравнение (2) можно перепи­сать так: 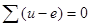. Здесь и—е — напряжение на ветви.

Следовательно, алгебраическая сумма напряжений на ветвях в лю­бом замкнутом контуре равна нулю.

Формулы (1) и (2) напи­саны в общем виде для мгновенных значений токов, напряжений и э.д.с; они справедливы для цепей как пе­ременного, так и постоянного тока.

Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.

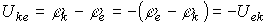
(4)

Просуммируем напряжения на ветвях некоторого контура:

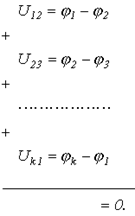
Поскольку при обходе контура потенциал каждой i-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.

Таким образом, второй закон Кирхгофа математически записывается, как:

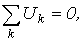
(5)

- и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается 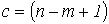независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из 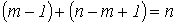уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.

Введем столбцовую матрицу напряжений ветвей

U=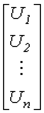

Тогда второй закон Кирхгофа в матричной форме записи имеет вид

BU = 0.

(6)

 

 

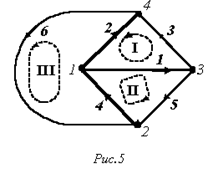В качестве примера для схемы рис. 5 имеем

,

откуда, например, для первого контура получаем

,

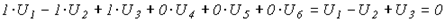что и должно иметь место.

Если ввести столбцовую матрицу узловых потенциалов

=

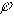причем потенциал последнего узла 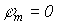, то матрица напряжений ветвей и узловых потенциалов связаны соотношением

U=AТ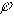

(7)

где A^Т - транспонированная узловая матрица.

Для определения матрицы В по известной матрице А=А_ДА_С , где А_Д – подматрица, соответствующая ветвям некоторого дерева, А_С- подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-А^Т_С А^-1Т_Д1).

 

4) Типы задач, решаемых при расчёте электрооборудования. Дуальность элементов

 

В рамках электротехники решаются 2 задачи: анализ и синтез (проектирование).

При проектировании различного рода устройств ав­томатического управления, каналов электропроводной и радиосвязи и т. п. возникает необходимость подбора схем и параметров электрических цепей, отвечающих оп­ределенным требованиям. Нахождение схемы и элемен­тов цепи, удовлетворяющей заданным условиям, состав­ляет задачу синтеза электрической цепи.

Ввиду того что установившийся и переходный про­цессы во всякой линейной электрической цепи зависят от частотных свойств цепи, задача синтеза обычно сводится к нахождению цепи по заданной частотной харак­теристике. Искомым может быть двухполюсник с задан­ной зависимостью сопротивления (или проводимости) от частоты либо четырехполюсник с заданной передаточной функцией или частотной зависимостью его параметров. Построение схемы пассивной цепи по заданной частотной функции принято называть реализацией или осу­ществлением функции.

В отличие от задачи анализа, в которой искомая ве­личина — реакция цепи на приложенное воздействие — получается однозначно, задача синтеза может иметь не­сколько решений (или вовсе не иметь решения). Задан­ная частотная функция считается реализуемой или осу­ществимой, если соответствующая ей электрическая цепь может быть составлена из сопротивлений, индуктивностей и емкостей (возможно также применение трансфор­маторов).

Поскольку задача синтеза может иметь несколько ре­шений, возникает необходимость сопоставления получен­ных вариантов и выбора оптимального решения.

В этом вопросе не имеется вполне определенного критерия, так как приходится сравнивать схемы с разно­родными элементами. При этом обычно руководствуются следующими соображениями. Желательны схемы с наи­меньшим количеством элементов, имеющие практически приемлемые параметры, причем предпочтение следует от­давать схемам, содержащим простейшие элементы — сопротивления и емкости.

Индуктивность — менее желательный элемент цепи. Если в схеме последовательно включены индуктивность и сопротивление, то они могут быть практически выпол­нены в виде индуктивной катушки. Однако при этом приходится считаться с витковой емкостью, которая мо­жет внести в работу цепи искажения при высоких ча­стотах.

Еще менее желательным элементом схемы является трансформатор, практическое осуществление которого сопряжено с появлением тепловых потерь и межвитковых емкостей. Кроме того, коэффициент связи может не совпадать с расчетным.

В задачах синтеза частотные характеристики сопро­тивлений, проводимостей или передаточных функций мо­гут быть заданы графически или аналитически. Если характеристика задана графически или не является рациональной функцией, то она приближенно аппроксимирует­ся рациональной функцией, т. е. отношением двух поли­номов, которое по определенным правилам синтеза реа­лизуется в виде двух- или четырехполюсника.

Таким образом, первым этапом в задаче синтеза яв­ляется аппроксимация заданной частотной характери­стики рациональной функцией; этот этап, относящийся к области математики, здесь не рассматривается. Второй этап заключается в реализации рациональной функции, что и составляет основное содержание данной главы.

Дуальность элементов

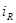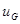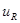Рассматривая соотношения (табл. 1.1), прихо­дим к заключению, что выражения, соответствующие попарно сопро­тивлению и проводимости, емкости и индуктивности, имеют подобную структуру. Если в выражениях, описывающих основные соотношения для сопротивления, заменить  на ,  на 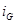, R на G, то получат­ся основные соотношения для проводимости. 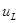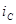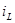Аналогично, выражения, описывающие основные соотношения для емкости и индуктивности, могут быть получены одно из другого путем замены  на ,  на 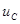, L на С.

Элементы, для которых основные соотношения имеют одинаковую структуру и могут быть получены одно из другого путем таких за­мен, называются дуальными. Таким образом, емкость и индуктивность, сопротивление и проводимость (попарно) являются дуальными элементами.

Свойством дуальности обладают не только рассмотренные идеа­лизированные пассивные элементы. Из последующих разделов будет видно, что дуальными также могут быть идеализированные активные элементы и электрические цепи, составленные из идеализированных активных и пассивных элементов.

В ряде случаев использование принципа дуальности позволяет облегчить исследование процессов в цепи. Так, если известны основные соотношения, описывающие процессы в некоторой цепи, то соответствующие соотношения для дуальной цепи могут быть получены без вывода, на основании использования свойства дуальности.

5) Метод эквивалентных преобразований

 

При расчетах сложных электрических цепей во многих случа­ях целесообразно производить их упрощение путем свертывания, заменяя отдельные участки цепи с последовательным, параллель­ным и смешанным соединениями сопротивлений одним эквива­лентным сопротивлением с помощью метода эквивалентных пре­образований (метода трансфигураций) электрических цепей.

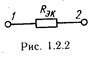
а) Электрическая цепь с последовательным соединением сопротивлений (рис. 1.2.1) заменяется при этом цепью с одним эквива­лентным сопротивлением R_экв (рис. 1.2.2), равным сумме всех сопротивлений цепи: 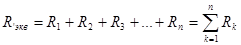, где 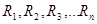 — сопротивления отдельных участков цепи. 

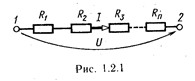
При этом ток I в электрической цепи сохраняет неизменным свое значение, все сопротивления обтекаются одним и тем же током. Напряжения (падения напряжения) на сопротивлениях при по­следовательном соединении их распределяются пропорционально сопротивлениям отдельных участков: .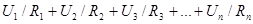

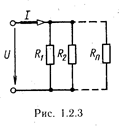
б) При параллельном соединении сопротивлений все сопро­тивления находятся под одним и тем же напряжением U (рис. 1.2.3). Электрическую цепь, состоящую из параллельно соединенных сопротивлений, целесообразно заменить цепью с эквивалентным сопротивлением R_экв (рис. 1.2.2), которое опреде­ляется из выражения 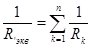, где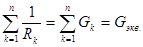

сумма величин, обратных сопротивлениям участков параллель­ных ветвей электрической цепи (сумма проводимостей ветвей цепи); R_K — сопротивление параллельного участка цепи; G_экв. — эквивалентная проводимость параллельного участка цепи, G_экв.=1/ R_экв; п — число параллельных ветвей цепи. Эквивалентное сопротивление участка цепи, состоящего из одинаковых парал­лельно соединенных сопротивлений, R_экв= R/ n.

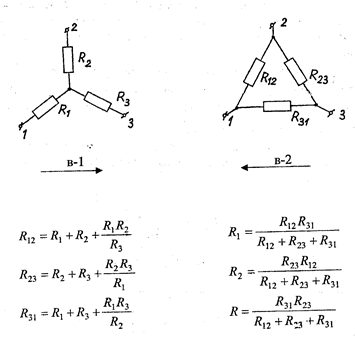
в) Во многих случаях оказывается целесообразным также преобра­зование сопротивлений, соединенных треугольником, эквивалентной звездой.