Основные понятия и величины, характеризующие электрические цепи
а) Понятия:
Электрической цепью называется совокупность устройств, предназначаемых для прохождения электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий напряжения и тока. В общем случае электрическая цепь состоит из источников и приемников электрической энергии и промежуточных звеньев (проводов, аппаратов), связывающих источники с приемниками.
Источниками электрической энергии являются устройства (гальванические элементы, аккумуляторы, термоэлементы, генераторы), в которых происходит процесс преобразования химической, молекулярно-кинетической, тепловой, механической или другого вида энергии в электрическую.
Приемниками электрической энергии (нагрузкой), служат устройства (электрические лампы, электронагревательные приборы, электрические двигатели, резисторы, конденсаторы, индуктивные катушки), в которых электрическая энергия превращается в световую, тепловую, механическую и др.
б) Величины:
Электрический ток и напряжение являются основными величинами, характеризующими состояние электрических цепей.
Электрический ток в проводниках представляет явление упорядоченного движения электрических зарядов. Под термином «ток» понимают также интенсивность или силу тока, измеряемую количеством электрического заряда q, прошедшего через, поперечное сечение проводника в единицу времени: 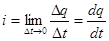
Следовательно, ток представляет собой скорость изменения заряда во времени. В СИ заряд выражается в кулонах (Кл), время—в секундах (с), ток — в амперах (А).
Ток как отношение двух скалярных величин является скалярной алгебраической величиной, знак которой зависит от направления движения зарядов одного знака, а именно условно принятого положительного заряда. Для однозначного определения знака тока за положительное направление достаточно произвольно выбрать одно из двух возможных направлений, которое отмечают стрелкой. 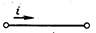
Если движение положительного заряда происходит в направлении стрелки, а движение отрицательного заряда—навстречу ей, то ток положителен. При изменении направления движения зарядов на противоположный ток будет отрицательным.
Задать однозначно ток в виде некоторой функции времени можно только после указания выбранного положительного направления тока. Поэтому перед началом анализа на всех участках цепи необходимо отметить положительные направления токов, выбор которых может быть произвольным.
Прохождение электрического тока или перенос зарядов в цепи связаны с преобразованием или потреблением энергии. Для определения энергии, затрачиваемой на перемещение заряда между двумя рассматриваемыми точками проводника, вводят новую величину—напряжение.
Напряжением называют количество энергии, затрачиваемой на перемещение единицы заряда из одной точки в другую: 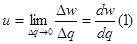 , где w—энергия.
, где w—энергия.
При измерении энергии в джоулях (Дж) и заряда в кулонах (Кл) напряжение выражают в вольтах (В).
Напряжение как отношение двух скалярных величин также является скалярной алгебраической величиной. Для однозначного определения знака напряжения между двумя выводами рассматриваемого участка цепи одному из выводов условно приписывают положительную полярность, которую отмечают либо стрелкой, направленной от вывода, либо знаками « + »,«—
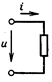
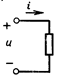 Напряжение положительно, если его полярность совпадает с выбранной; это означает, что потенциал вывода со знаком « + », из которого выходит стрелка, выше потенциала второго вывода.
Напряжение положительно, если его полярность совпадает с выбранной; это означает, что потенциал вывода со знаком « + », из которого выходит стрелка, выше потенциала второго вывода.
Перед началом анализа должны быть указаны выбранные положительные полярности напряжений — только при этом условии возможно однозначное определение напряжений.
Хотя условно положительную полярность напряжения можно выбирать произвольно, обычно удобно выбирать ее согласованной с выбранным положительным направлением тока, когда стрелки для тока и напряжения совпадают или знак « + » полярности напряжения находится в хвосте стрелки, обозначающей положительное направление тока. При согласованном выборе полярности, очевидно, достаточно ограничиться указанием только одной стрелки положительного направления тока.
Если возникает необходимость выбора положительной полярности напряжения, не согласованной с положительным направлением тока, то приходится указывать две встречно направленные стрелки: для тока и для напряжения. Это не очень удобно. Поэтому для обозначения условно положительной полярности будем применять знаки «+.», « —» у выводов участка цепи.
Из определения напряжения (1) получаем выражение энергии, затраченной на перемещение заряда q на участке цепи с напряжением и к моменту времени t.
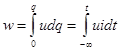 . Здесь суммируются все энергетические процессы при действии напряжения, начиная от t = — ∞, где энергия принимается равной нулю, до рассматриваемого момента. Дифференцирование этого равенства по времени дает выражение скорости изменения энергии во времени, т. е. мощности, выражаемой в ваттах:
. Здесь суммируются все энергетические процессы при действии напряжения, начиная от t = — ∞, где энергия принимается равной нулю, до рассматриваемого момента. Дифференцирование этого равенства по времени дает выражение скорости изменения энергии во времени, т. е. мощности, выражаемой в ваттах: 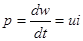
Мощность в электрической цепи, равная произведению напряжения на ток, также является алгебраической величиной. Знак ее определяется знаками напряжения и тока: при совпадении этих знаков мощность положительна, что соответствует потреблению энергии в рассматриваемом участке цепи; при несовпадении знаков напряжения и тока мощность отрицательна, что означает отдачу ее из участка цепи (такой участок является источником энергии).
Закон Ома
Сопротивление есть отношение напряжения на данном элементе цепи к току, проходящему через него. 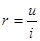 .Основными законами теории цепей наряду с законом Ома являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа).
.Основными законами теории цепей наряду с законом Ома являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа).
Распределение токов и напряжений в электрических цепях подчиняется законам Кирхгофа.
Первый закон Кирхгофа
Алгебраическая сумма токов в узле равна нулю: 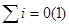
Суммирование распространяется на токи в ветвях, сходящихся в рассматриваемом узле. При этом знаки токов берутся с учетом выбранных положительных направлений токов: всем токам, направленным от узла, в уравнении (1) приписывается одинаковый знак, например положительный, и соответственно все токи, направленные к узлу, входят в уравнение (1) с противоположным знаком.
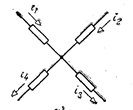 На рис. в качестве примера показан узел, в котором сходятся четыре ветви. Уравнение (1) имеет в этом случае вид:— i1 — i2+ i3+ i4=0.
На рис. в качестве примера показан узел, в котором сходятся четыре ветви. Уравнение (1) имеет в этом случае вид:— i1 — i2+ i3+ i4=0.
Первый закон Кирхгофа выражает тот факт, что в узле электрический заряд не накапливается и не расходуется.Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
Первый закон Кирхгофа применим не только к узлу, но и к любому контуру или замкнутой поверхности, охватывающей часть электрической цепи, так как ни в каком элементе цепи, ни в каком режиме электричество одного знака не может накапливаться.
Так, например, для схемы
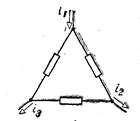 имеем: — i1+ i2+ i3=0.
имеем: — i1+ i2+ i3=0.
Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение
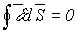
| (1) |
где 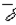 - вектор плотности тока;
- вектор плотности тока; 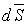 - нормаль к участку dS замкнутой поверхности S.
- нормаль к участку dS замкнутой поверхности S.
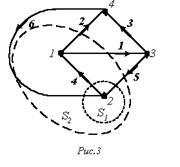
Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S2 графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать
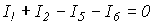 .
.
Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:
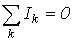
| (2) |
т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.
При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.
Введем столбцовую матрицу токов ветвей
| I= | 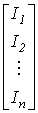
|
Тогда первый закон Кирхгофа в матричной форме записи имеет вид:
| АI=O | (3) |
– где O - нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не АН, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.
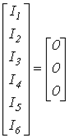
В качестве примера запишем для схемы на рис. 3
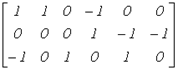
| 
|
Отсюда для первого узла получаем
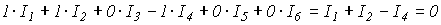 ,
,
что и должно иметь место.
Второй закон Кирхгофа
Алгебраическая сумма э.д.с. в любом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура: 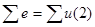 .
.
Обход контура совершается в произвольно выбранном направлении, например по ходу часовой стрелки. При этом соблюдается следующее правило знаков для э.д.с. и падений напряжения, входящих в (2): э.д.с. и падения напряжения, совпадающие по направлению с направлением обхода, берутся с одинаковыми знаками.
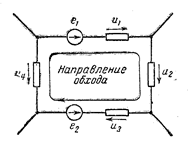 Например, для данной схемы
Например, для данной схемы 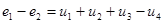 .Уравнение (2) можно переписать так:
.Уравнение (2) можно переписать так: 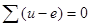 . Здесь и—е — напряжение на ветви.
. Здесь и—е — напряжение на ветви.
Следовательно, алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.
Формулы (1) и (2) написаны в общем виде для мгновенных значений токов, напряжений и э.д.с; они справедливы для цепей как переменного, так и постоянного тока.
Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.
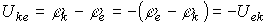
| (4) |
Просуммируем напряжения на ветвях некоторого контура:
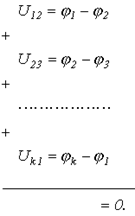
Поскольку при обходе контура потенциал каждой i-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.
Таким образом, второй закон Кирхгофа математически записывается, как:
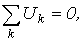
| (5) |
- и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается 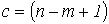 независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из
независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из 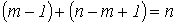 уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
Введем столбцовую матрицу напряжений ветвей
| U= | 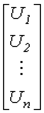
|
Тогда второй закон Кирхгофа в матричной форме записи имеет вид
| BU = 0. | (6) |
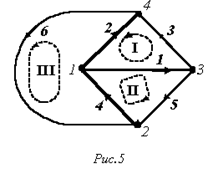 В качестве примера для схемы рис. 5 имеем
В качестве примера для схемы рис. 5 имеем
 ,
,
откуда, например, для первого контура получаем
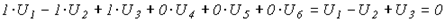 ,
,
что и должно иметь место.
Если ввести столбцовую матрицу узловых потенциалов
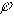 = =
| 
|
причем потенциал последнего узла 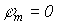 , то матрица напряжений ветвей и узловых потенциалов связаны соотношением
, то матрица напряжений ветвей и узловых потенциалов связаны соотношением
U=AТ 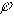
| (7) |
где AТ - транспонированная узловая матрица.
Для определения матрицы В по известной матрице А=АДАС , где АД – подматрица, соответствующая ветвям некоторого дерева, АС- подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-АТС А-1ТД1).
4) Типы задач, решаемых при расчёте электрооборудования. Дуальность элементов
В рамках электротехники решаются 2 задачи: анализ и синтез (проектирование).
При проектировании различного рода устройств автоматического управления, каналов электропроводной и радиосвязи и т. п. возникает необходимость подбора схем и параметров электрических цепей, отвечающих определенным требованиям. Нахождение схемы и элементов цепи, удовлетворяющей заданным условиям, составляет задачу синтеза электрической цепи.
Ввиду того что установившийся и переходный процессы во всякой линейной электрической цепи зависят от частотных свойств цепи, задача синтеза обычно сводится к нахождению цепи по заданной частотной характеристике. Искомым может быть двухполюсник с заданной зависимостью сопротивления (или проводимости) от частоты либо четырехполюсник с заданной передаточной функцией или частотной зависимостью его параметров. Построение схемы пассивной цепи по заданной частотной функции принято называть реализацией или осуществлением функции.
В отличие от задачи анализа, в которой искомая величина — реакция цепи на приложенное воздействие — получается однозначно, задача синтеза может иметь несколько решений (или вовсе не иметь решения). Заданная частотная функция считается реализуемой или осуществимой, если соответствующая ей электрическая цепь может быть составлена из сопротивлений, индуктивностей и емкостей (возможно также применение трансформаторов).
Поскольку задача синтеза может иметь несколько решений, возникает необходимость сопоставления полученных вариантов и выбора оптимального решения.
В этом вопросе не имеется вполне определенного критерия, так как приходится сравнивать схемы с разнородными элементами. При этом обычно руководствуются следующими соображениями. Желательны схемы с наименьшим количеством элементов, имеющие практически приемлемые параметры, причем предпочтение следует отдавать схемам, содержащим простейшие элементы — сопротивления и емкости.
Индуктивность — менее желательный элемент цепи. Если в схеме последовательно включены индуктивность и сопротивление, то они могут быть практически выполнены в виде индуктивной катушки. Однако при этом приходится считаться с витковой емкостью, которая может внести в работу цепи искажения при высоких частотах.
Еще менее желательным элементом схемы является трансформатор, практическое осуществление которого сопряжено с появлением тепловых потерь и межвитковых емкостей. Кроме того, коэффициент связи может не совпадать с расчетным.
В задачах синтеза частотные характеристики сопротивлений, проводимостей или передаточных функций могут быть заданы графически или аналитически. Если характеристика задана графически или не является рациональной функцией, то она приближенно аппроксимируется рациональной функцией, т. е. отношением двух полиномов, которое по определенным правилам синтеза реализуется в виде двух- или четырехполюсника.
Таким образом, первым этапом в задаче синтеза является аппроксимация заданной частотной характеристики рациональной функцией; этот этап, относящийся к области математики, здесь не рассматривается. Второй этап заключается в реализации рациональной функции, что и составляет основное содержание данной главы.
Дуальность элементов
Рассматривая соотношения (табл. 1.1), приходим к заключению, что выражения, соответствующие попарно сопротивлению и проводимости, емкости и индуктивности, имеют подобную структуру. Если в выражениях, описывающих основные соотношения для сопротивления, заменить 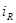 на
на 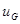 ,
, 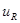 на
на 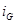 , R на G, то получатся основные соотношения для проводимости. Аналогично, выражения, описывающие основные соотношения для емкости и индуктивности, могут быть получены одно из другого путем замены
, R на G, то получатся основные соотношения для проводимости. Аналогично, выражения, описывающие основные соотношения для емкости и индуктивности, могут быть получены одно из другого путем замены 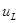 на
на 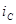 ,
, 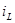 на
на 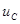 , L на С.
, L на С.
Элементы, для которых основные соотношения имеют одинаковую структуру и могут быть получены одно из другого путем таких замен, называются дуальными. Таким образом, емкость и индуктивность, сопротивление и проводимость (попарно) являются дуальными элементами.
Свойством дуальности обладают не только рассмотренные идеализированные пассивные элементы. Из последующих разделов будет видно, что дуальными также могут быть идеализированные активные элементы и электрические цепи, составленные из идеализированных активных и пассивных элементов.
В ряде случаев использование принципа дуальности позволяет облегчить исследование процессов в цепи. Так, если известны основные соотношения, описывающие процессы в некоторой цепи, то соответствующие соотношения для дуальной цепи могут быть получены без вывода, на основании использования свойства дуальности.
5) Метод эквивалентных преобразований
При расчетах сложных электрических цепей во многих случаях целесообразно производить их упрощение путем свертывания, заменяя отдельные участки цепи с последовательным, параллельным и смешанным соединениями сопротивлений одним эквивалентным сопротивлением с помощью метода эквивалентных преобразований (метода трансфигураций) электрических цепей.
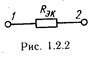
а) Электрическая цепь с последовательным соединением сопротивлений (рис. 1.2.1) заменяется при этом цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.2.2), равным сумме всех сопротивлений цепи: 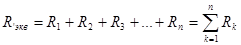 , где
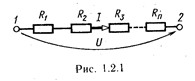
, где 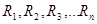 — сопротивления отдельных участков цепи.
— сопротивления отдельных участков цепи.
 При этом ток I в электрической цепи сохраняет неизменным свое значение, все сопротивления обтекаются одним и тем же током. Напряжения (падения напряжения) на сопротивлениях при последовательном соединении их распределяются пропорционально сопротивлениям отдельных участков:
При этом ток I в электрической цепи сохраняет неизменным свое значение, все сопротивления обтекаются одним и тем же током. Напряжения (падения напряжения) на сопротивлениях при последовательном соединении их распределяются пропорционально сопротивлениям отдельных участков: 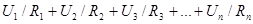 .
.
б) При параллельном соединении сопротивлений все сопротивления находятся под одним и тем же напряжением U (рис. 1.2.3). Электрическую цепь, состоящую из параллельно соединенных сопротивлений, целесообразно заменить цепью с эквивалентным сопротивлением Rэкв (рис. 1.2.2), которое определяется из выражения 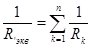 , где
, где 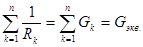
сумма величин, обратных сопротивлениям участков параллельных ветвей электрической цепи (сумма проводимостей ветвей цепи); RK — сопротивление параллельного участка цепи; Gэкв. — эквивалентная проводимость параллельного участка цепи, Gэкв.=1/ Rэкв; п — число параллельных ветвей цепи. Эквивалентное сопротивление участка цепи, состоящего из одинаковых параллельно соединенных сопротивлений, Rэкв= R/ n.
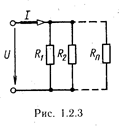 в) Во многих случаях оказывается целесообразным также преобразование сопротивлений, соединенных треугольником, эквивалентной звездой.
в) Во многих случаях оказывается целесообразным также преобразование сопротивлений, соединенных треугольником, эквивалентной звездой.
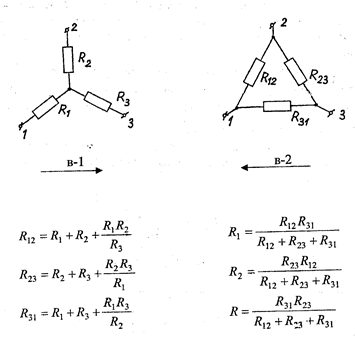
Метод контурных токов
Этот метод позволяет уменьшить количество уравнений системы, составляемых по законам Кирхгофа, до 
где nв– число ветвей цепи;
ny– число узлов цепи;
nm– число источников тока цепи.
Он основан на том, что ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При использовании метода перед расчётом выбирают направления и путь протекания контурных токов - по любой ветви должен протекать хотя бы один выбранный контурный ток. Общее число неизвестных контурных токов определяется величиной k (1). Причём, из пути их протекания следует исключить ветви с источниками тока.
Пример:
Исходные данные:
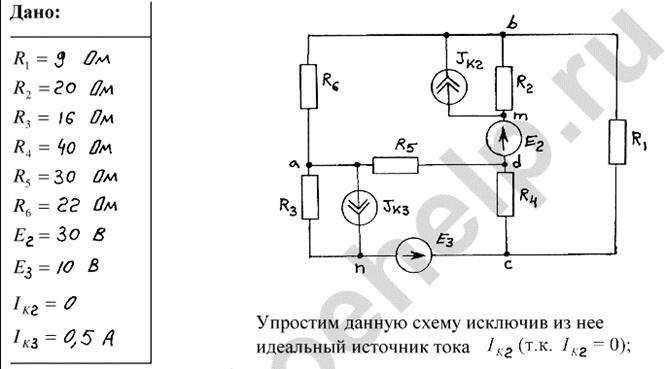
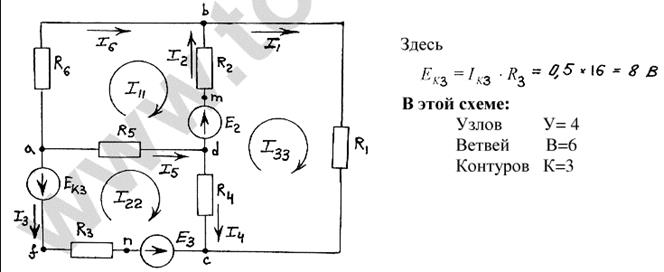
R1 =24 Ом; R2=70 Ом; R3=44 Ом; R4=12 Ом; R5=20 Ом; R6=30 Ом; Е2=40 В; Е3=19,6 В; JK2=0 А; JK3=0,1 А.

При расчёте этой схемы методом контурных токов возможны два пути:
1) Преобразование исходной схемы не производится.
2) Предусматривает преобразование реальных источников тока в эквивалентную э.д.с.
Для расчёта данной схемы выбираем второй путь и при этом учтём, что
JK2=0 А. Преобразуем JK3 в E3*. Пользуясь законом Ома, получаем E3*= JK3R3=4,4 B.
Схема, полученная после преобразования представлена на рисунке 2.
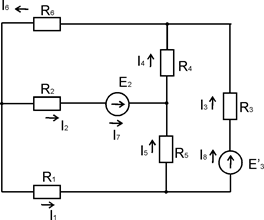
Рисунок 2 – Преобразованная схема
E3’=E3+ E3*=19,6+4,4=24(B)
После упрощения исходной схемы можно непосредственно перейти к реализации метода контурных токов. Для этого нужно определить количество контурных токов. Сделать это можно по формуле:
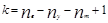
где nв– число ветвей цепи;
ny– число узлов цепи;
nm– число источников тока цепи.
В рассматриваемой схеме nв=6, ny=4; nm=0.
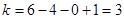
Итак, зная количество контурных токов, нужно выбрать их направления.
Схема с направлениями контурных токов представлена на рисунке 3.
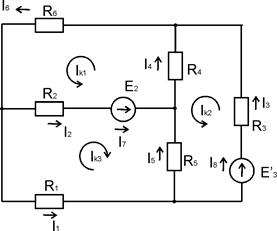
Рисунок 3 – Преобразованная схема с направлениями контурных токов
Составим систему уравнений по второму закону Кирхгофа для определения неизвестных контурных токов (порядок системы равен k):
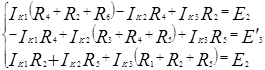
Составим матрицу:
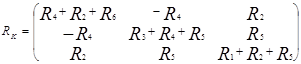


Отсюда выразим матрицу контурных токов:
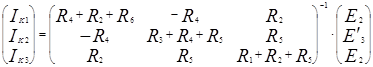
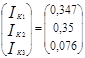
Зная значения контурных токов, можно найти реальные токи. Они будут равны комбинации контурных токов.
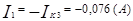
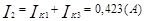
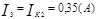
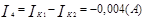
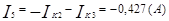
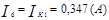
Используя контурные токи, мы получили токи конкретные.
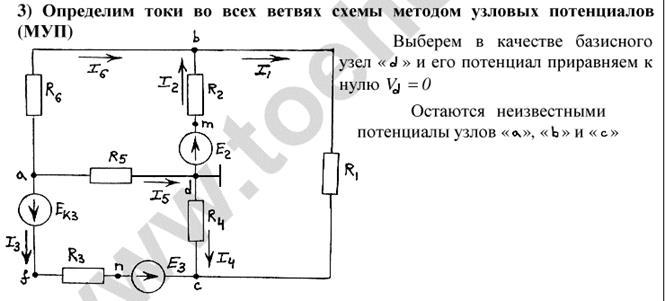
10) Метод узловых напряжений (потенциалов)




Полная мощность
Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:
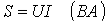 . .
| (6) |
Активная, реактивная и полная мощности связаны следующим соотношением:
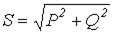 . .
| (7) |
Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности 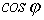 равен косинусу угла сдвига между током и напряжением. Итак,
равен косинусу угла сдвига между током и напряжением. Итак,
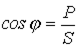 . .
| (8) |
Комплексная мощность
Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть 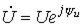 , а
, а 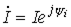 . Тогда комплекс полной мощности:
. Тогда комплекс полной мощности:
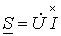 , ,
| (9) |
где 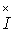 - комплекс, сопряженный с комплексом
- комплекс, сопряженный с комплексом 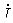 .
.
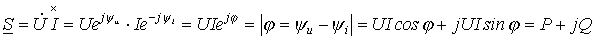 .
.
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует 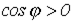 (активно-индуктивная нагрузка), для которого имеем:
(активно-индуктивная нагрузка), для которого имеем:
.
Применение статических конденсаторов для повышения cos 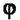
Как уже указывалось, реактивная мощность  циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению
циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению 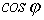 в силовых электрических цепях.
в силовых электрических цепях.
Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.
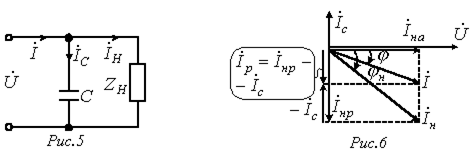
Если параллельно такой нагрузке 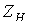 (см. рис. 5), включить конденсатор С, то общий ток
(см. рис. 5), включить конденсатор С, то общий ток 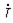 , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е.
, как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. 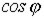 увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности
увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности 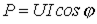 . На этом основано применение конденсаторов для повышения
. На этом основано применение конденсаторов для повышения 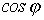 .
.
Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения 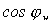 до значения
до значения 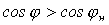 ?
?
Разложим 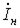 на активную
на активную 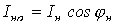 и реактивную
и реактивную 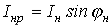 составляющие. Ток через конденсатор
составляющие. Ток через конденсатор  компенсирует часть реактивной составляющей тока нагрузки
компенсирует часть реактивной составляющей тока нагрузки 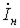 :
:
 ; ;
| (10) |
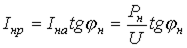 ; ;
| (11) |
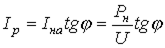 . .
| (12) |
Из (11) и (12) с учетом (10) имеем
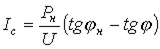 ,
,
но 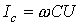 , откуда необходимая для повышения
, откуда необходимая для повышения 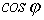 емкость:
емкость:
 . .
| (13) |
Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
а) Постоянный ток
Для любой цепи постоянного тока выполняется соотношение:
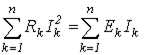
| (14) |
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
б) Переменный ток.
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
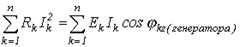
| (15) |
В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:
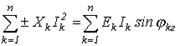 , ,
| (16) |
где знак “+” относится к индуктивным элементам 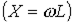 , “-” – к емкостным
, “-” – к емкостным 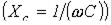 .
.
Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):
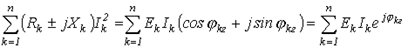
или
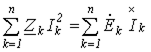 .
.
Решение
1. Строим результирующую ВАХ 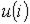 цепи (см. рис. 4) согласно соотношению
цепи (см. рис. 4) согласно соотношению
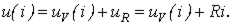
2. Находя для различных значений  с использованием полученной кривой соответствующие им значения тока, строим по точкам (см. рис. 5) кривую искомой зависимости
с использованием полученной кривой соответствующие им значения тока, строим по точкам (см. рис. 5) кривую искомой зависимости 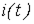 .
.
К полученному результату необходимо сделать следующий комментарий. Использование при анализе подобных цепей ВАХ идеального вентиля (обратный ток отсутствует, в проводящем направлении падение напряжения на диоде равно нулю) корректно при достаточно больших значениях амплитуд приложенного к диоду напряжения, определяющих значительное превышение током, протекающим через вентиль в прямом направлении, его обратного тока, вследствие чего последним можно пренебречь. При снижении величин напряжения, когда эти токи становятся сопоставимыми по величине, следует использовать ВАХ реального диода,представленную на рис. 4 и учитывающую наличие обратного тока.
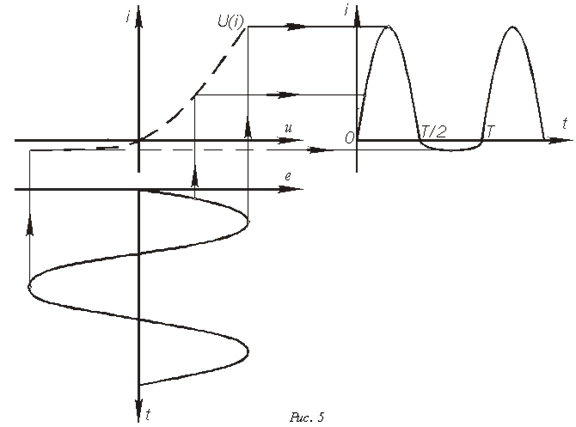
Важнейшим элементом в цепях переменного тока является катушка с ферромагнитным сердечником. В общем случае кривая зависимости 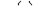 имеет вид гистерезисной петли, но, поскольку в устройствах, работающих при переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную (или начальную) кривую намагничивания.
имеет вид гистерезисной петли, но, поскольку в устройствах, работающих при переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную (или начальную) кривую намагничивания.
Условное изображение нелинейной катушки индуктивности приведено на рис. 6. Здесь 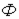 – основной поток, замыкающийся по сердечнику,
– основной поток, замыкающийся по сердечнику,  - поток рассеяния, которому в первом приближении можно поставить в соответствие потокосцепление рассеяния
- поток рассеяния, которому в первом приближении можно поставить в соответствие потокосцепление рассеяния  , где индуктивность рассеяния
, где индуктивность рассеяния  в силу прохождения потоком
в силу прохождения потоком 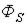 части пути по воздуху.
части пути по воздуху.
Для схемы на рис. 6 справедливо уравнение
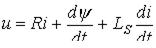 , ,
| (1) |
где 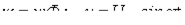 .
.
В общем случае в силу нелинейности зависимости 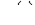 определить на основании (1) несинусоидальные зависимости
определить на основании (1) несинусоидальные зависимости 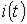 и
и 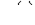 достаточно непросто. Вместе с тем для реальных катушек индуктивности падением напряжения
достаточно непросто. Вместе с тем для реальных катушек индуктивности падением напряжения 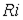 и ЭДС, обусловленной потоками рассеивания, вследствие их малости, часто можно пренебречь. При этом из (1) получаем
и ЭДС, обусловленной потоками рассеивания, вследствие их малости, часто можно пренебречь. При этом из (1) получаем 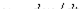 , откуда
, откуда
 ,
,
где  постоянная интегрирования.
постоянная интегрирования.
Так как характеристика  катушки (см. рис. 7) симметрична относительно начала координат, а напряжение
катушки (см. рис. 7) симметрична относительно начала координат, а напряжение 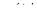 симметрично относительно оси абсцисс (оси времени), то кривая
симметрично относительно оси абсцисс (оси времени), то кривая 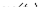 также должна быть симметричной относительно последней, откуда следует, что
также должна быть симметричной относительно последней, откуда следует, что 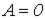 .
.
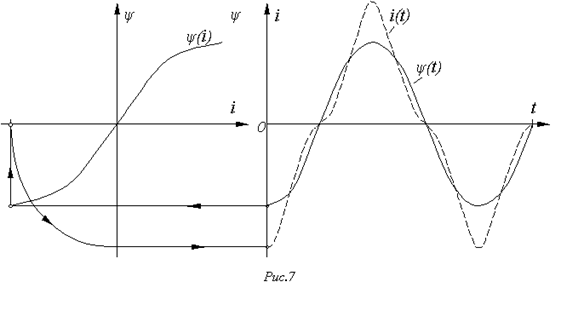
Находя для различных значений 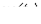 с использованием кривой
с использованием кривой 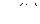 соответствующие им значения тока, строим по точкам (см. рис. 7) кривую зависимости
соответствующие им значения тока, строим по точкам (см. рис. 7) кривую зависимости  .
.
Анализ полученного результата позволяет сделать важный вывод: при синусоидальной форме потока напряжение 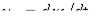 на катушке синусоидально, а протекающий через нее ток имеет явно выраженную несинусоидальную форму. Аналогично можно показать, что при синусоидальном токе поток, сцепленный с катушкой, и напряжение на ней несинусоидальны.
на катушке синусоидально, а протекающий через нее ток имеет явно выраженную несинусоидальную форму. Аналогично можно показать, что при синусоидальном токе поток, сцепленный с катушкой, и напряжение на ней несинусоидальны.
Для среднего значения напряжения, наведенного потоком, можно записать
 . .
| (2) |
Умножив (2) на коэффициент формы, получим выражение для действующего значения напряжения
. 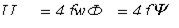
В частности, если напряжение и поток синусоидальны, то
 .
.
Соотношение (2) является весьма важным: измеряя среднее значение напряжения, наведенного потоком, по (2) можно определить амплитуды потока 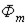 и индукции
и индукции 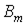 при любой форме нелинейности катушки.
при любой форме нелинейности катушки.
Аналогично проводится построение кривой  при синусоидальном потоке и задании зависимости
при синусоидальном потоке и задании зависимости 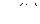 в виде петли гистерезиса. При этом следует помнить, что перемещение рабочей точки по петле осуществляется против часовой стрелки (см. рис. 8).
в виде петли гистерезиса. При этом следует помнить, что перемещение рабочей точки по петле осуществляется против часовой стрелки (см. рис. 8).
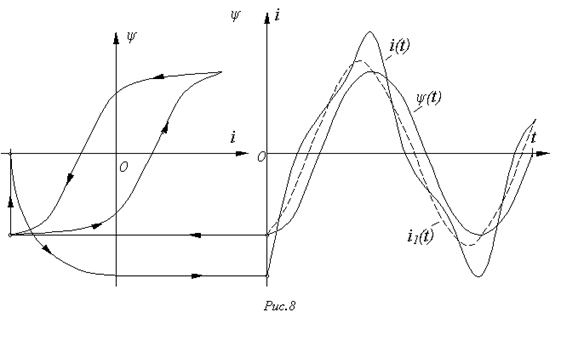 К полученному результату следует сделать следующий важный комментарий. Разложение построенной кривой
К полученному результату следует сделать следующий важный комментарий. Разложение построенной кривой  в ряд Фурье показывает, что первая гармоника тока (см. кривую
в ряд Фурье показывает, что первая гармоника тока (см. кривую  на рис. 8) опережает по фазе потокосцепление и, следовательно, отстает по фазе от синусоидального напряжения на катушке на угол, меньший 90°. Это указывает (
на рис. 8) опережает по фазе потокосцепление и, следовательно, отстает по фазе от синусоидального напряжения на катушке на угол, меньший 90°. Это указывает ( 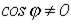 ) на потребление катушкой активной мощности, затрачиваемой на перемагничивание сердечника и определяемой площадью петли гистерезиса.
) на потребление катушкой активной мощности, затрачиваемой на перемагничивание сердечника и определяемой площадью петли гистерезиса.
Магнитные цепи
При решении электротехнических задач все вещества в магнитном отношении делятся на две группы:
- ферромагнитные (относительная магнитная проницаемость
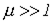 );
); - неферромагнитные (относительная магнитная проницаемость
 ).
).
Для концентрации магнитного поля и придания ему желаемой конфигурации отдельные части электротехнических устройств выполняются из ферромагнитных материалов. Эти части называют магнитопроводами или сердечниками. Магнитный поток создается токами, протекающими по обмоткам электротехнических устройств, реже – постоянными магнитами. Совокупность устройств, содержащих ферромагнитные тела и образующих замкнутую цепь, вдоль которой замыкаются линии магнитной индукции, называют магнитной цепью.
Магнитное поле характеризуется тремя векторными величинами, которые приведены в табл. 1.
Таблица 1. Векторные величины, характеризующие магнитное поле
| Наименование | Обозначение | Единицы измерения | Определение |
| Вектор магнитной индукции | 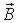
| Тл (тесла) | Векторная величина, характеризующая силовое действие магнитного поля на ток по закону Ампера |
| Вектор намагниченности | 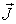
| А/м | Магнитный момент единицы объема вещества |
| Вектор напряженности магнитного поля | 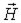
| А/м |   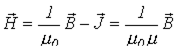 ,
где ,
где   Гн/м- магнитная постоянная Гн/м- магнитная постоянная
|
Основные скалярные величины, используемые при расчете магнитных цепей, приведены в табл. 2.
Таблица 2. Основные скалярные величины, характеризующие магнитную цепь
| Наименование | Обозначение | Единица измерения | Определение |
| Магнитный поток | 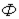
| Вб (вебер) | Поток вектора магнитной индукции через поперечное сечение 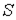 магнитопровода магнитопровода
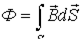
|
| Магнитодвижущая (намагничивающая) сила МДС (НС) | 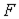
| A | 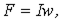 где где 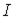 -ток в обмотке, -ток в обмотке, 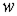 -число витков обмотки -число витков обмотки
|
| Магнитное напряжение | 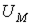
| А | Линейный интеграл от напряженности магнитного поля 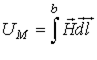 , где , где 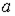 и и 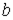 -граничные точки участка магнитной цепи, для которого определяется -граничные точки участка магнитной цепи, для которого определяется 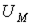
|
Регулярные методы расчета
Данными методами решаются задачи первого типа -”прямые” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и основные геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала и магнитный поток или магнитная индукция в каком-либо сечении магнитопровода. Требуется найти НС, токи обмоток или, при известных значениях последних, число витков.
Графические методы расчета
Графическими методами решаются задачи второго типа - “обратные” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала, а также НС обмоток. Требуется найти значения потоков (индукций) на отдельных участках магнитопровода.
Данные методы основаны на графическом представлении вебер-амперных характеристик 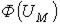 линейных и нелинейных участков магнитной цепи с последующим решением алгебраических уравнений, записанных по законам Кирхгофа, с помощью соответствующих графических построений на плоскости.
линейных и нелинейных участков магнитной цепи с последующим решением алгебраических уравнений, записанных по законам Кирхгофа, с помощью соответствующих графических построений на плоскости.
Итерационные методы расчета
Данные методы, сущность которых была рассмотрена при анализе нелинейных резистивных цепей постоянного тока, являются приближенными численными способами решения нелинейных алгебраических уравнений, описывающих состояние магнитной цепи. Как было отмечено выше, они хорошо поддаются машинной алгоритмизации и в настоящее время широко используются при исследовании сложных магнитных цепей на ЦВМ. При анализе относительно простых цепей, содержащих небольшое число узлов и нелинейных элементов в эквивалентной электрической схеме замещения (обычно до двух-трех), возможна реализация методов “вручную”.
В качестве примера приведем алгоритм расчета магнитной цепи на рис. 1, в которой при заданных геометрии магнитопровода, характеристике 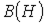 материала сердечника и величине НС F необходимо найти поток Ф.
материала сердечника и величине НС F необходимо найти поток Ф.
В соответствии с пошаговым расчетом для данной цепи можно записать
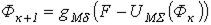 , ,
| (1) |
где 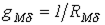 .
.
Задаемся значением 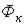 , вычисляем для
, вычисляем для 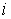 -х участков магнитопровода
-х участков магнитопровода 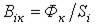 , по кривой намагничивания
, по кривой намагничивания  находим
находим 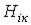 , подсчитываем
, подсчитываем 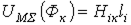 и по (1) определяем
и по (1) определяем 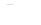 для следующего приближения и т.д., пока с заданной погрешностью не будет выполняться равенство
для следующего приближения и т.д., пока с заданной погрешностью не будет выполняться равенство  .
.
Б) Устройство машины постоянного тока
Машина постоянного тока в основном состоит из неподвижной части, служащей для возбуждения главного магнитного поля, и вращающейся части, в которой индуктируется ЭДС. Токи от этой ЭДС, взаимодействуя с главным магнитным полем, создают тормозной момент в генераторном режиме и вращающий момент в двигательном.
 Неподвижная часть состоит из станины (рис. 13.1), на которой укрепляются основные (главные) полюсы для возбуждения главного
Неподвижная часть состоит из станины (рис. 13.1), на которой укрепляются основные (главные) полюсы для возбуждения главного
магнитного потока и дополнительные для улучшения коммутации в машине.
Главный полюс состоит из сердечника полюса, набранного из листовой стали и укрепленного болтами на станине, и катушки обмотки возбуждения. Сердечник на свободном конце снабжается полюсным наконечником для создания требуемого распределения магнитной индукции вдоль окружности якоря.
Станина является ярмом машины, т. е. частью, замыкающей магнитную цепь главного потока Ф (рис. 13.2). Она изготовляется из литой стали, так как магнитный поток в ней относительно постоянен. Дополнительные полюсы устанавливаются на станине между основными. На сердечниках дополнительных полюсов располагаются обмотки, которые соединяются последовательно с якорем.
Якорем называют часть машины, в обмотке которой при вращении ее относительно главного магнитного поля индуктируется ЭДС. В машине постоянного тока якорь состоит из зубчатого сердечника, обмотки, уложенной в его пазах, и коллектора, насаженного на вал якоря. Сердечник якоря набирается из листов электротехнической стали (рис. 13.3, а) толщиной 0,5 мм, изолированных друг от друга лаком.
В пазы сердечника якоря уложена обмотка якоря (рис. 13.3, б) обычно состоящая из отдельных секций. Для отвода тока от коллектора служат щетки, установленные в щеткодержателях (рис. 13.4). Щетку 1 к коллектору прижимает пружина 2. Ток от щетки отводится специальным гибким кабелем. Щеткодержатели надеваются на щеточную траверсу (отверстие 3), от которой они электрически изолируются. Траверса крепится соосно с якорем так, что ее  можно поворачивать, изменяя положение щеток по отношению к полюсам машины.
можно поворачивать, изменяя положение щеток по отношению к полюсам машины.


 Характерной частью электрических машин постоянного тока является коллектор. Это полый цилиндр, собранный из изолированных друг от друга клинообразных медных пластин 1 (рис. 13.5). Пластины коллектора изолированы также от вала машины. Проводниками 2 они соединяются с витками обмотки, размещенной в пазах якоря.
Характерной частью электрических машин постоянного тока является коллектор. Это полый цилиндр, собранный из изолированных друг от друга клинообразных медных пластин 1 (рис. 13.5). Пластины коллектора изолированы также от вала машины. Проводниками 2 они соединяются с витками обмотки, размещенной в пазах якоря.
Вращающаяся обмотка соединяется с внешней цепью скользящим контактом между щетками и коллектором.
Как и все электрические машины, машина постоянного тока обратима. Она работает в режиме генератора, если ее вращает первичный двигатель, главное магнитное поле возбуждено, а цепь якоря соединена через щетки с приемником. При таких условиях ЭДС, индуктируемая в обмотке якоря, создает в якоре и приемнике ток.
Взаимодействие тока якоря с главным магнитным полем создает на валу машины тормозной момент, который преодолевается первичным двигателем. Генератор преобразует механическую энергию в электрическую.
В двигательном режиме цепи якоря и возбуждения машины присоединены к источнику электроэнергии. Взаимодействие тока якоря с главным магнитным полем создает вращающий момент. Под действием последнего вращающийся якорь преодолевает момент нагрузки на валу машины. Двигатель преобразует электрическую энергию в механическую.
Таким образом, одна и та же машина может быть использована в качестве генератора или двигателя. Важнейшим классификационным признаком машин постоянного тока является способ возбуждения главного магнитного поля. Одним из них является использование постоянных магнитов на полюсах машины. Во многих современных машинах главное магнитное поле возбуждается с помощью электромагнитов. Для этого используется обмотка возбуждения с током возбуждения, размещенная на сердечниках полюсов машины. Все рабочие характеристики машин постоянного тока при работе как в режиме генератора, так и в режиме двигателя зависят от способа включения цепи возбуждения по отношению к цепи якоря. Соединение этих цепей может быть параллельным, последовательным, смешанным, и, наконец, цепи эти могут быть независимы одна от другой, в соответствии с чем принято различать параллельное, последовательное, смешанное и независимое возбуждение машин. Практически весьма ценно то обстоятельство, что мощность цепи возбуждения при любом способе включения обмотки возбуждения относительно мала — примерно 5% номинальной мощности у малых машин и менее 1 % — у машин большой мощности. Это делает возможным экономичное управление работой машины постоянного тока (напряжением генератора, угловой скоростью вращения двигателя).
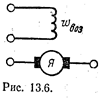
В машинах с независимым возбуждением обмотка возбуждения подключается к независимому источнику электроэнергии (рис. 13.6), благодаря чему ток в ней не зависит от напряжения на выводах якоря машины. Сечение проводов обмотки возбуждения в этих машинах выбирается в зависимости от напряжения источника тока возбуждения. Характерным для этих машин является независимость главного магнитного потока от нагрузки машины.
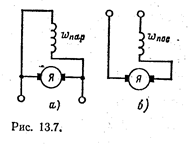
У машин с параллельным возбуждением цепь обмотки возбуждения соединяется параллельно с цепью якоря (рис. 13.7, а). В этом случае ток возбуждения Iв во много раз меньше тока якоря (0,05—0,01), а напряжение U между выводами цепей якоря и возбуждения одно и то же. Следовательно, сопротивление
обмотки возбуждения (rв= U/ Iв) должно быть относительно велико. Обмотка возбуждения машины параллельного возбуждения имеет большое число витков wnа p из тонкого провода и благодаря этому обладает значительным сопротивлением. Характерно для машин параллельного возбуждения, работающих в системе большой мощности, постоянство главного магнитного потока и его небольшая зависимость от условий нагрузки машины.
У машин с последовательным возбуждением ток якоря Iя равен току обмотки возбуждения (рис. 13.7, б), поэтому она выполняется проводом большого сечения. Значение тока Iя в обмотке последовательного
возбуждения велико, благодаря чему для получения необходимой МДС (Iя wnoс) достаточно, чтобы эта обмотка имела малое число витков wnoс. Следовательно, сопротивление обмотки последовательного возбуждения rв относительно мало. Для этих машин характерны изменения в широких пределах главного магнитного потока при изменениях нагрузки машины вследствие изменений тока якоря, который является одновременно и током возбуждения.
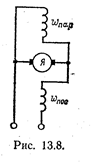
В машинах со смешанным возбуждением на каждом полюсном сердечнике расположены две обмотки (рис. 13.8)
Одна из этих обмоток, подключаемая параллельно якорю, является основной. Создаваемая ею МДС (Iпар wпар) возбуждает главное магнитное поле.
Вторая обмотка wnoс лишь дополнительно воздействует на это магнитное поле. В зависимости от преобладания МДС, созданных последовательной или параллельной обмоткой возбуждения, машина по своим характеристикам может быть машиной последовательного возбуждения с небольшой параллельной обмоткой возбуждения или машиной параллельного возбуждения с небольшой последовательной обмоткой возбуждения. В большинстве машин смешанного возбуждения применяется согласное соединение, т. е. МДС двух обмоток складываются. Встречное соединение, при котором МДС обмоток имеют противоположное направление, применяется в немногих специальных случаях.
Б) Рабочие характеристики
Механическая характеристика наглядно показывает свойства асинхронного двигателя как части электропривода. Но для более полного выявления свойств самого двигателя служат его рабочие характеристики— так принято называть зависимости от полезной мощности Р2 двигателя на валу частоты вращения п, вращающего момента М, коэффициента мощности cosφ и КПД η = 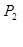 . Все рабочие характеристики снимаются при номинальных частоте сети f и напряжении между выводами статора U1 = U1ном.
. Все рабочие характеристики снимаются при номинальных частоте сети f и напряжении между выводами статора U1 = U1ном.
 Так как
Так как 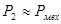 , а
, а 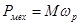 то зависимость n(Р2) — скоростная характеристика — мало отличается по форме от механической характеристики двигателя п (М), она тоже может быть названа жесткой (рис. 14.29). Вращающий момент М, развиваемый двигателем, складывается из полезного момента M2 (преодоления нагрузки на валу двигателя) и момента холостого хода Мх. Последний затрачивается на покрытие механических потерь двигателя. Этот момент можно приближенно считать не зависящим от нагрузки двигателя. Полезный момент
то зависимость n(Р2) — скоростная характеристика — мало отличается по форме от механической характеристики двигателя п (М), она тоже может быть названа жесткой (рис. 14.29). Вращающий момент М, развиваемый двигателем, складывается из полезного момента M2 (преодоления нагрузки на валу двигателя) и момента холостого хода Мх. Последний затрачивается на покрытие механических потерь двигателя. Этот момент можно приближенно считать не зависящим от нагрузки двигателя. Полезный момент 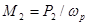 и если бы
и если бы 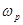 была строго постоянна, то зависимость
была строго постоянна, то зависимость 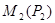 была бы линейна, но угловая скорость двигателя немного уменьшается с увеличением Р2, поэтому график зависимости М2 (Р2) немного отклоняется вверх. Соответственно график вращающего момента М (Р2), складывающегося из момента холостого хода и полезного момента, пересекает ось ординат в точке, соответствующей Мх, а затем он почти прямолинеен и лишь немного изгибается вверх.
была бы линейна, но угловая скорость двигателя немного уменьшается с увеличением Р2, поэтому график зависимости М2 (Р2) немного отклоняется вверх. Соответственно график вращающего момента М (Р2), складывающегося из момента холостого хода и полезного момента, пересекает ось ординат в точке, соответствующей Мх, а затем он почти прямолинеен и лишь немного изгибается вверх.
Что касается зависимости 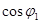 двигателя от нагрузки, то его изменения обусловлены следующими соотношениями. Намагничивающий ток двигателя мало зависит от нагрузки, так как ее увеличение вызывает лишь возрастание потокосцеплений рассеяния, пропорциональных токам в обмотках статора и ротора, а главный магнитный поток машины при возрастании нагрузки незначительно уменьшается. Но активный ток двигателя пропорционален его механической нагрузке. Таким образом, с увеличением нагрузки двигателя относительное значение реактивного тока быстро убывает, a
двигателя от нагрузки, то его изменения обусловлены следующими соотношениями. Намагничивающий ток двигателя мало зависит от нагрузки, так как ее увеличение вызывает лишь возрастание потокосцеплений рассеяния, пропорциональных токам в обмотках статора и ротора, а главный магнитный поток машины при возрастании нагрузки незначительно уменьшается. Но активный ток двигателя пропорционален его механической нагрузке. Таким образом, с увеличением нагрузки двигателя относительное значение реактивного тока быстро убывает, a 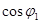 увеличивается. При холостом ходе двигателя его коэффициент мощности довольно низок — примерно 0,2. С увеличением нагрузки он быстро возрастает и достигает максимального значения (0,7—0,9) при нагрузке, близкой к номинальной. Таким образом, даже у полностью загруженного двигателя реактивный ток составляет 70—40 % тока статора.
увеличивается. При холостом ходе двигателя его коэффициент мощности довольно низок — примерно 0,2. С увеличением нагрузки он быстро возрастает и достигает максимального значения (0,7—0,9) при нагрузке, близкой к номинальной. Таким образом, даже у полностью загруженного двигателя реактивный ток составляет 70—40 % тока статора.
Неполная загруженность асинхронных двигателей является одной из главных причин низкого cos <p промышленных предприятий. Естественным способом повышения cosφ является полная загрузка асинхронных двигателей. Главный магнитный поток двигателя пропорционален напряжению на статоре. Намагничивающий ток, возбуждающий этот поток, при заданном значении потока обратно пропорционален магнитному сопротивлению на пути потока. В этом магнитном сопротивлении большую часть составляет сопротивление воздушного зазора между статором и ротором. По этой причине конструктор стремится сократить этот зазор до минимума, определяемого условиями подвижности в подшипниках и необходимым запасом на их износ, прогибом вала и точностью центровки. С увеличением номинальной мощности двигателя необходимый воздушный зазор возрастает значительно медленнее этой мощности, благодаря чему с повышением номинальной мощности двигателя его cos q> увеличивается. С уменьшением номинальной частоты вращения двигателя увеличивается его магнитный поток, так как при меньшей частоте вращения он индуктирует в фазной обмотке статора меньшую ЭДС. Следовательно, у тихоходных двигателей намагничивающий ток относительно больше, a cosφ существенно меньше.
Коэффициент полезного действия определяется отношением полезной мощности на валу Р2 к мощности Р1 определяющей потребление двигателем энергии из сети: 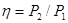
Мощность Р1 равна сумме полезной мощности и мощности всех потерь в двигателе: 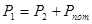
Мощность всех потерь энергии в двигателе можно разделить на постоянную составляющую, практически не зависящую от нагрузки, и переменную составляющую, зависящую от нее.
Мощностью постоянных потерь энергии в двигателе можно считать мощность потерь в сердечнике статора на гистерезис и вихревые токи и мощность механических потерь, которая определяется экспериментально из опыта холостого хода двигателя.
Мощностью переменных потерь энергии в двигателе является мощность потерь на нагревание проводников обмоток статора и ротора, она равна: 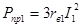
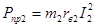
Своего максимального значения (65—95 %) КПД достигает, когда переменные потери равны постоянным. У большинства двигателей этот максимум КПД имеет место примерно при нагрузке, равной 75 % номинальной, так как двигатели проектируются с учетом того обстоятельства, что далеко не всегда они полностью загружены.
Основные понятия и величины, характеризующие электрические цепи
а) Понятия:
Электрической цепью называется совокупность устройств, предназначаемых для прохождения электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий напряжения и тока. В общем случае электрическая цепь состоит из источников и приемников электрической энергии и промежуточных звеньев (проводов, аппаратов), связывающих источники с приемниками.
Источниками электрической энергии являются устройства (гальванические элементы, аккумуляторы, термоэлементы, генераторы), в которых происходит процесс преобразования химической, молекулярно-кинетической, тепловой, механической или другого вида энергии в электрическую.
Приемниками электрической энергии (нагрузкой), служат устройства (электрические лампы, электронагревательные приборы, электрические двигатели, резисторы, конденсаторы, индуктивные катушки), в которых электрическая энергия превращается в световую, тепловую, механическую и др.
б) Величины:
Электрический ток и напряжение являются основными величинами, характеризующими состояние электрических цепей.
Электрический ток в проводниках представляет явление упорядоченного движения электрических зарядов. Под термином «ток» понимают также интенсивность или силу тока, измеряемую количеством электрического заряда q, прошедшего через, поперечное сечение проводника в единицу времени: 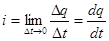
Следовательно, ток представляет собой скорость изменения заряда во времени. В СИ заряд выражается в кулонах (Кл), время—в секундах (с), ток — в амперах (А).
Ток как отношение двух скалярных величин является скалярной алгебраической величиной, знак которой зависит от направления движения зарядов одного знака, а именно условно принятого положительного заряда. Для однозначного определения знака тока за положительное направление достаточно произвольно выбрать одно из двух возможных направлений, которое отмечают стрелкой. 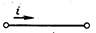
Если движение положительного заряда происходит в направлении стрелки, а движение отрицательного заряда—навстречу ей, то ток положителен. При изменении направления движения зарядов на противоположный ток будет отрицательным.
Задать однозначно ток в виде некоторой функции времени можно только после указания выбранного положительного направления тока. Поэтому перед началом анализа на всех участках цепи необходимо отметить положительные направления токов, выбор которых может быть произвольным.
Прохождение электрического тока или перенос зарядов в цепи связаны с преобразованием или потреблением энергии. Для определения энергии, затрачиваемой на перемещение заряда между двумя рассматриваемыми точками проводника, вводят новую величину—напряжение.
Напряжением называют количество энергии, затрачиваемой на перемещение единицы заряда из одной точки в другую: 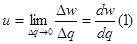 , где w—энергия.
, где w—энергия.
При измерении энергии в джоулях (Дж) и заряда в кулонах (Кл) напряжение выражают в вольтах (В).
Напряжение как отношение двух скалярных величин также является скалярной алгебраической величиной. Для однозначного определения знака напряжения между двумя выводами рассматриваемого участка цепи одному из выводов условно приписывают положительную полярность, которую отмечают либо стрелкой, направленной от вывода, либо знаками « + »,«—

 Напряжение положительно, если его полярность совпадает с выбранной; это означает, что потенциал вывода со знаком « + », из которого выходит стрелка, выше потенциала второго вывода.
Напряжение положительно, если его полярность совпадает с выбранной; это означает, что потенциал вывода со знаком « + », из которого выходит стрелка, выше потенциала второго вывода.
Перед началом анализа должны быть указаны выбранные положительные полярности напряжений — только при этом условии возможно однозначное определение напряжений.
Хотя условно положительную полярность напряжения можно выбирать произвольно, обычно удобно выбирать ее согласованной с выбранным положительным направлением тока, когда стрелки для тока и напряжения совпадают или знак « + » полярности напряжения находится в хвосте стрелки, обозначающей положительное направление тока. При согласованном выборе полярности, очевидно, достаточно ограничиться указанием только одной стрелки положительного направления тока.
Если возникает необходимость выбора положительной полярности напряжения, не согласованной с положительным направлением тока, то приходится указывать две встречно направленные стрелки: для тока и для напряжения. Это не очень удобно. Поэтому для обозначения условно положительной полярности будем применять знаки «+.», « —» у выводов участка цепи.
Из определения напряжения (1) получаем выражение энергии, затраченной на перемещение заряда q на участке цепи с напряжением и к моменту времени t.
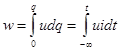 . Здесь суммируются все энергетические процессы при действии напряжения, начиная от t = — ∞, где энергия принимается равной нулю, до рассматриваемого момента. Дифференцирование этого равенства по времени дает выражение скорости изменения энергии во времени, т. е. мощности, выражаемой в ваттах:
. Здесь суммируются все энергетические процессы при действии напряжения, начиная от t = — ∞, где энергия принимается равной нулю, до рассматриваемого момента. Дифференцирование этого равенства по времени дает выражение скорости изменения энергии во времени, т. е. мощности, выражаемой в ваттах: 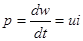
Мощность в электрической цепи, равная произведению напряжения на ток, также является алгебраической величиной. Знак ее определяется знаками напряжения и тока: при совпадении этих знаков мощность положительна, что соответствует потреблению энергии в рассматриваемом участке цепи; при несовпадении знаков напряжения и тока мощность отрицательна, что означает отдачу ее из участка цепи (такой участок является источником энергии).
Классификация электрических цепей и их элементов. Виды схем, используемых в электротехнике
а) Классификация электрических цепей
1) Электрические цепи делятся на простые и сложные. К признакам, определяющим простую цепь, можно отнести:
- наличие только одного источника энергии (сигнала);
- возможность до расчётов указать истинные направления токов во всех ветвях;
- соединение элементов цепи выполнено по правилам последовательного, параллельного и смешанного соединений.
Отсутствие любого из этих признаков может переводить цепь в категорию сложных.
Последовательное- соединение группы идеализированных двухполюсных элементов, при котором через них протекает один и тот же ток.
Параллельное- соединение группы идеализированных двухполюсных элементов, при котором все элементы находятся под одним и тем же напряжением.
Смешанное- комбинация последовательного и параллельного соединений
Для анализа простых цепей используется два метода:
- метод свёртки схемы цепи относительно зажимов источника (он же метод определения входного или эквивалентного сопротивления);
- метод пропорциональных (определяющих) величин.
Методы анализа сложных цепей, например - метод контурных токов (МКТ) и метод узловых напряжений (МУН).
2) В зависимости от характера соединения идеализированных двухполюсных элементов различают неразветвлённые и разветвлённые цепи.
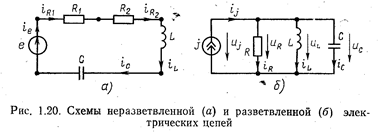 В неразветвлённой цепи через все элементы протекает один и тот же ток. В разветвлённой цепи токи через различные элементы могут быть не одинаковы.
В неразветвлённой цепи через все элементы протекает один и тот же ток. В разветвлённой цепи токи через различные элементы могут быть не одинаковы.
3) В теории электрических цепей различают активные и пассивные элементы. Соответственно различают активные и пассивные цепи.
4) Цепь, составленная целиком из линейных элементов, называется линейной.
Цепь, содержащая хотя бы один нелинейный элемент, называется нелинейной.
б) Классификация элементов
Под элементами в теории электрических цепей подразумеваются обычно не физически существующие составные части электротехнических устройств, а их идеализированные модели, которым
теоретически приписываются определенные электрические и магнитные свойства, так что они в совокупности приближенно отображают явления, происходящие в реальных устройствах.
В теории электрических цепей различают активные и пассивные элементы. Соответственно различают активные и пассивные цепи.
Элементы электрической цепи, осуществляющие преобразование других видов энергии в электромагнитную, расходуемую и запасаемую в других элементах, называются источниками или активными элементами цепи. Активными элементами считаются источники электрической энергии: источники напряжения и источники тока.
Элементы цепи, осуществляющие необратимое потребление электромагнитной энергии или ее накопление, являются пассивными элементами. К пассивным элементам электрических цепей относятся сопротивления, индуктивности и емкости.
Пассивные элементы. Необратимое потребление энергии с преобразованием ее в тепловую,, механическую, химическую, акустическую осуществляется в резистивном элементе R .
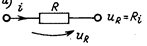 При согласованных направлениях отсчета тока и напряжения, указанных на рисунке, имеем связь, выражаемую законом Ома: uR = Ri, где R— сопротивление элемента — параметр, выражающий интенсивность потребления энергии. Независимо от направления тока и закона его изменения во времени потребляемая резистором мощность и энергия положительны:
При согласованных направлениях отсчета тока и напряжения, указанных на рисунке, имеем связь, выражаемую законом Ома: uR = Ri, где R— сопротивление элемента — параметр, выражающий интенсивность потребления энергии. Независимо от направления тока и закона его изменения во времени потребляемая резистором мощность и энергия положительны: 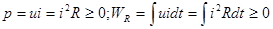
Накопление энергии в магнитном поле осуществляется в индуктивном элементе L, в котором при протекании тока i, изменяющегося во времени, изменяется потокосцепление ψ= Li и наводится ЭДС (е = — dψ/ dt).
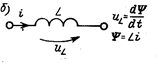 Параметр L — индуктивность— определяет интенсивность накопления энергии. Для преодоления ЭДС е к зажимам элемента от внешних источников должно быть приложено напряжение uL= — e= d ψ/ dt. Следует обратить внимание на то, что знак в выражении для напряжения определяется согласованным выбором направлений отсчета напряжения и тока, указанным на рис.. Индуктивный элемент потребляет энергию при положительных значениях dWL = uidt = idψ, когда энергия магнитного поля
Параметр L — индуктивность— определяет интенсивность накопления энергии. Для преодоления ЭДС е к зажимам элемента от внешних источников должно быть приложено напряжение uL= — e= d ψ/ dt. Следует обратить внимание на то, что знак в выражении для напряжения определяется согласованным выбором направлений отсчета напряжения и тока, указанным на рис.. Индуктивный элемент потребляет энергию при положительных значениях dWL = uidt = idψ, когда энергия магнитного поля 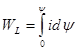 = J idW возрастает, и отдает ее при dW = idψ < 0.
= J idW возрастает, и отдает ее при dW = idψ < 0.
Процесс накопления энергии в электрическом поле осуществляется в емкостном элементе С, ток которого определяется скоростью изменения заряда на обкладках элемента, который, в свою очередь, связан с напряжением между обкладками выражением 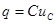 , где С — емкость элемента.
, где С — емкость элемента.
Элемент потребляет энергию 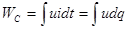 = и dq при
= и dq при 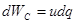 > 0 и отдает ее при udq < 0.
> 0 и отдает ее при udq < 0.
Зависимости u( i) резистора, ψ( i) индуктивной катушки, q (и) конденсатора — характеристики элементов — в общем случае имеют нелинейный характер. Обладающие такими характеристиками элементы называются нелинейными. При линейности соответствующей характеристики параметры R, L или С постоянны, и элементы называются линейными.
Цепь, составленная целиком из линейных элементов, называется линейной. Энергия, накапливаемая в линейных элементах L и С, выражается как 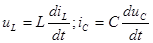
Цепь, содержащая хотя бы один нелинейный элемент, называется нелинейной.
Активные элементы. Реальные источники энергии часто работают в одном из следующих режимов:
1) во всем диапазоне допустимых значении тока напряжение на зажимах мало зависит от протекающего тока;
2) наоборот, в рабочем диапазоне ток, генерируемый источником, мало зависит от напряжения на его зажимах.
Идеализация свойств источников 1-го типа приводит к источнику ЭДС е — элементу, напряжение на зажимах которого не зависит от протекающего через этот источник тока i, а определяется лишь внутренними свойствами источника. Стрелка внутри кружка, схематически изображающего источник ЭДС, показывает направление действия ЭДС — направление, в котором за счет преобразования энергии осуществляется перемещение положительных зарядов внутри источника.
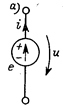 В результате на верхнем зажиме источника образуется избыток положительных, а на нижнем зажиме — отрицательных зарядов. Эти обозначения также используют для маркировки зажимов источника ЭДС. В результате вне источника между его зажимами возникает напряжение. При использовании изображенного стрелкой на рис. направления отсчета напряжения имеем и=е. Принятое направление отсчета и соответствует направлению линий напряженности электрического поля, возникающего в окружающем источник пространстве. Эти линии, не показанные на рис., направлены от верхнего зажима источника к нижнему. Если к зажимам источника присоединить пассивный элемент, то это электрическое поле вызовет движение положительных зарядов во внешней цепи — электрический ток i в направлении стрелки. Идеализация свойств источников 2-го типа — это источник тока, ток которого J не зависит от напряжения и на его зажимах.
В результате на верхнем зажиме источника образуется избыток положительных, а на нижнем зажиме — отрицательных зарядов. Эти обозначения также используют для маркировки зажимов источника ЭДС. В результате вне источника между его зажимами возникает напряжение. При использовании изображенного стрелкой на рис. направления отсчета напряжения имеем и=е. Принятое направление отсчета и соответствует направлению линий напряженности электрического поля, возникающего в окружающем источник пространстве. Эти линии, не показанные на рис., направлены от верхнего зажима источника к нижнему. Если к зажимам источника присоединить пассивный элемент, то это электрическое поле вызовет движение положительных зарядов во внешней цепи — электрический ток i в направлении стрелки. Идеализация свойств источников 2-го типа — это источник тока, ток которого J не зависит от напряжения и на его зажимах.
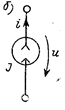 Разумеется, оба указанных типа источников не могут быть реализованы на практике, так как всегда имеет место зависимость напряжения источника ЭДС или тока источника тока от режима нагрузки. Это обстоятельство иногда подчеркивают, называя рассмотренные виды источников идеальными источниками.
Разумеется, оба указанных типа источников не могут быть реализованы на практике, так как всегда имеет место зависимость напряжения источника ЭДС или тока источника тока от режима нагрузки. Это обстоятельство иногда подчеркивают, называя рассмотренные виды источников идеальными источниками.
При описании свойств компонентов электронных цепей (например, биполярных и полевых транзисторов) возникает необходимость ввести так называемые управляемые (зависимые) источники ЭДС и тока, параметры которых в отличие от рассмотренных выше независимых источников зависят от напряжений или токов на других участках рассматриваемой электрической цепи. Можно ввести четыре типа управляемых источников.
1) Источник напряжения, управляемый напряжением (ИНУН) или усилитель напряжения.
2) Источник напряжения, управляемый током (ИНУТ)
3) Источник тока, управляемый напряжением (ИТУН).
3) Источник тока, управляемый током (ИТУТ) или усилитель тока.
Дата: 2019-05-29, просмотров: 394.