Чтобы получить пятиугольную область допустимых значений выберем k=11.2.
Подставив коэффициенты a, b, c, k, получим функцию
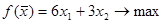
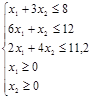
Построим область допустимых значений
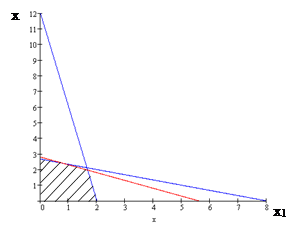 |
Рисунок 4.1 – Область допустимых значений
Чтобы получить максимум целевой функции будем ее переносить параллельно самой себе до пересечения с крайней точкой области допустимых значений. В данном случае максимум находится в точке пересечения функций 6x1+x2=12 и 2x1+4x2=11,2.
Решим систему уравнений:
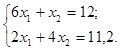
Получим точку максимума целевой функции:
Значение функции в этой точке f(x1,x2)=15,927
Решение задачи линейного программирования симплекс-методом
Приведем задачу к стандартной форме записи:
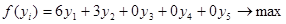
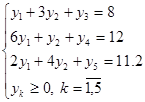
Начальный базис y0(0 0 8 12 11.2).
Процедура поиска оптимальной точки симплекс-методом сведена в таблицу 1.
Таблица 1. Симплекс-таблица
| Номер итерации | Базисные переменные | Значение | y1 | y2 | y3 | y4 | y5 | отношения |
| 0 | y3 | 8 | 1 | 3 | 1 | 0 | 0 | 0,125 |
| y4 | 12 | 6 | 1 | 0 | 1 | 0 | 0,5 | |
| y5 | 11,2 | 2 | 4 | 0 | 0 | 1 | 0,17857143 | |
| -f' | 0 | 6 | 3 | 0 | 0 | 0 | ||
| 1 | y3 | 6 | 0 | 2,833333 | 1 | -0,16667 | 0 | 0,4722 |
| y1 | 2 | 1 | 0,166667 | 0 | 0,166667 | 0 | 0,0833 | |
| y5 | 7,2 | 0 | 3,666667 | 0 | -0,33333 | 1 | 0,5093 | |
| -f' | -12 | 0 | 2 | 0 | -1 | 0 | ||
| 2 | y3 | 0,436363636 | 0 | 0 | 1 | 0,090909 | -0,77273 | |
| y1 | 1,672727273 | 1 | 0 | 0 | 0,181818 | -0,04545 | ||
| y2 | 1,963636364 | 0 | 1 | 0 | -0,09091 | 0,272727 | ||
| -f' | -15,92727273 | 0 | 0 | 0 | -0,81818 | -0,54545 |
На шаге 2 нет положительных коэффициентов в симплекс разности, значит, решение прекращаем.
Получаем оптимальное значение целевой функции
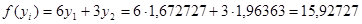
Определение оптимальных параметров технического объекта
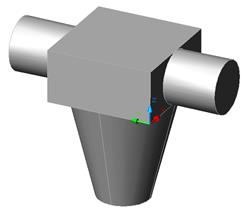
Рисунок 5.1-Модель сосуда
Параметры сосуда (рис.5.1):
Высота цилиндров – h1
Высота параллелепипеда – h2
Высота усеченного конуса – h3
Длина параллелепипеда – а
Ширина параллелепипеда – а
Радиус нижнего основания усеченного конуса – R
Радиус верхнего основания усеченного конуса – r
Соотношения параметров:
2h1 = 2h2 = h3 = H
a = 2R = 4r = x
Для того, чтобы рассчитать максимальный объем при заданной площади поверхности надо найти общую площадь сосуда
Площадь поверхности цилиндра: 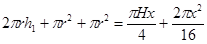
Площадь поверхности параллелепипеда: 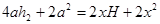
Площадь поверхности усеченного конуса:

Общая площадь боковой поверхности:

При заданной площади поверхности S=10 м2 выразим H из последнего уравнения
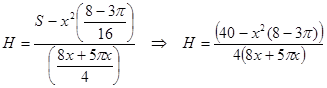
Найдем объем сосуда
Объем цилиндра: 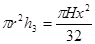
Объем параллелепипеда: 
Объем усеченного конуса: 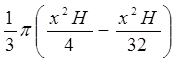
Общий объем сосуда равен:

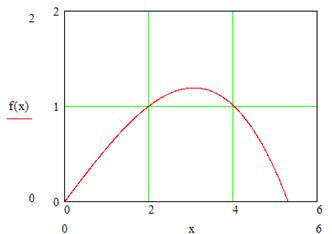
Рисунок 5.2
Подставив H в последнее уравнение, получим зависимость объема сосуда от одного параметра x. Зависимость и график функции представлен на рисунке 2. Область определения функции 1 четверть, т.к. объем и радиус – положительные величины. Для нахождения максимума функции воспользуемся методом золотого сечения.
Таким образом, максимальный объем при площади поверхности равной
10 м2 равен 1,19 м3
Заключение
В ходе выполнения данной курсовой работы нам удалось решить следующие задачи:
1. проведен анализ методов однопараметрический безусловной оптимизации;
2. проведен анализ методов многопараметрический безусловной оптимизации;
3. были разобраны основы линейного программирования;
4. был смоделирован и оптимизирован трёхмерный объект;
Список использованной литературы
1. Дегтярев Ю.И., «Исследование операций», Москва 1986;
2. Турчак Л.И., «Основы численных методов», Москва 1987;
3. Мудров А.Е., «Численные методы», Томск 1991;
4. Щетинин Е.Ю., «Математические методы оптимизации»;
Дата: 2019-05-29, просмотров: 287.