Алгоритм, описанный выше, можно модифицировать, добавив к процедуре отражения при построении нового симплекса процедуры сжатия и растяжения. Положение новой вершины находится сравнением и выбором наименьшего среди значений целевой функции в точках;
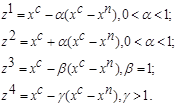(3.5)
Так как величина a Î (0; 1), то выбор точек z1 и z2 соответствует сжатию симплекса; b » 1, поэтому выбор точки z3 соответствует отражению, а g > 1 и выбор точки z4 приводит к растяжению симплекса. На практике хорошо зарекомендовал себя следующий набор параметров a, b и g для выбора пробных точек zi: a = 1/2, b = 1 и g =2.
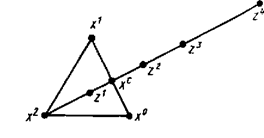
Рис. 3.2. Пробные точки z1,z2,z3,z4 для перехода к новому симплексу
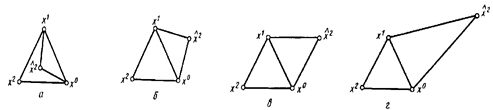
Рис. 3.3. Новые симлексы полученные в результате процедур сжатия (а,б); отражения (в); растяжения(г).
Опишем алгоритм метода поиска точки минимума функции по деформируемому симплексу.
Шаг 0 – Шаг 3 Аналогичны методу правильного симплекса.
Шаг 4. Найти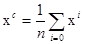 
и пробные точки zk , k =1, …, 4 пo формулам (3.5). Найти f (z*)= min f (zk). Если f (z*) < f (zn). то положить xn=z* и перейти к шагу 2. Иначе – перейти к шагу 5.
Поиск точки min методом циклического покоординатного спуска
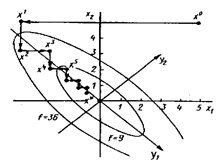
Этот метод заключается в последовательной минимизации целевой функции f (x) сначала по направлению первого базисного вектора е1, затем второго – е2 и т.д. После окончания минимизации по направлению последнего базисного вектора еn цикл повторяется.
Опишем этот алгоритм.
Шаг 0. Выбрать х Î En , критерий достижения точности, величину e. Найти f (x), положить j = 1.
Шаг 1. Решить задачу одномерной минимизации Ф(a) = f (х + aеj)® min, a Î R, т.е. найти a*. Положить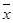 
= х +a*еj, вычислить f (х).
Шаг 2. Если j < п, то положить х = 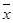, j=j+1 и перейти к шагу 1, иначе – перейти к шагу 3.
Шаг 3. Проверить условие достижения точности ||х–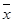 
|| < e
Поиск точки min методом Хука – Дживса
Этот алгоритм содержит две основные процедуры:
а) исследующий покоординатный поиск в окрестности данной точки, предназначенный для определения направления убывания f (х);
б) перемещение в направлении убывания.
Опишем алгоритм исследующего покоординатного поиска из заданной точки х с приращениями по каждой координате Dj , j = 1, …, n
Шаг 1. Положить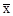 
= x , i = 1.
Шаг 2. Сделать пробный шаг y=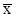 
– Dje j, где e j –j–й базисный вектор. Если f ( 
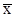) £ f (y), то перейти к шагу 3, иначе – к шагу 4.
Шаг 3. Сделать пробный шаг y= 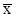+Dje j . Если f ( 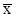) £ f (y), то перейти к шагу 5, иначе – к шагу 4.
Шаг 4. Положить 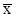= у.
Шаг 5 . Положить j = j + 1. Если j £ n, то перейти к шагу 2. В противном случае исследующий поиск окончен – получена точка 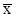для которой f ( 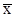) < f (y), если 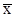¹ х.
Пример решения методами правильного симплекса, деформируемого симплекса, покоординатного спуска, Хука – Дживса
Дана функция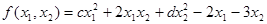 
, с=7; d=7.
Найти минимум функции с точностью ε=0,001
Метод правильного симплекса
Выбираем длину стороны треугольника l=10ε=0,0001
Вершины треугольника находим следующим образом:
A(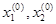 
);
B(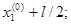 
);
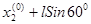D(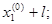 
).
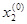A(1,065; 0,918);
B(1,07,0,927);
D(1,075,0,918).
Шаг 0
F(A)=10,903; F(B)=11,081; F(D)=11,051.
F1<F2<F3:
F1=F(A); F2=F(D); F3=F(B).
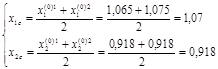
Отражаем вершину 3 относительно центра тяжести.
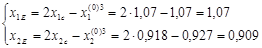
F(E)=10,873.
Значение функции в найденной точке меньше, значения функции в точке 1, поэтому принимаем новый симплекс (1,2,E).
Шаг 1
F(1)=10,903; F(2)=11,081; F(E)=10,873.
F1<F2<F3:
F1=F(E); F2=F(1); F3=F(2).
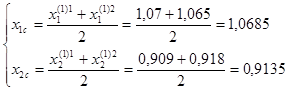
Отражаем вершину 3 относительно центра тяжести.
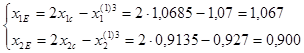
F(E)=10,726.
Значение функции в найденной точке меньше, значения функции в точке 1, поэтому принимаем новый симплекс (1,2,E).
,
.
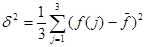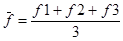В результате получаем x1=0,125, x2=0,208, f(x1, x2)=-0,41.
Метод деформируемого симплекса
Выбираем длину стороны треугольника l=5ε=0,005
Вершины треугольника находим следующим образом:
A(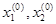 
);
B(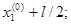 
);
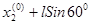D( ).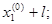
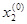A(1,065; 0,918);
B(1,07,0,927);
D(1,075,0,918).
Принимаем коэффициенты выбора пробных точек k1=0,5, k2=1, k3=2.
Шаг 0
F(A)=10,903; F(B)=11,081; F(D)=11,051.
F1<F2<F3:
F1=F(A); F2=F(D); F3=F(B).
Находим центр тяжести вершины 3 относительно вершин 1 и 2:
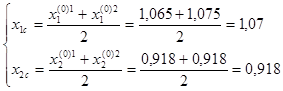
Выбираем пробные точки:
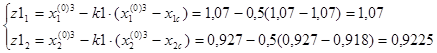
F(z1)=10,966.
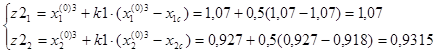
F(z2)=11,018.
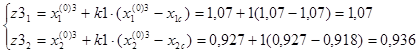
F(z3)=11,044.
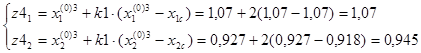
F(z3)=11,097.
Значение функции в z1 точке меньше, значения функции в точке 3, поэтому принимаем новый симплекс (1,2,z1).
Шаг 1
F(1)= 10,903; F(2)= 11,051; F(z1)=10,966.
F1<F2<F3:
F1=F(1); F2=F(z1); F3=F(2).
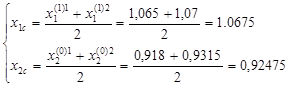
Выбираем пробные точки:
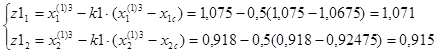
F(z1)=10,955.
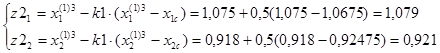
F(z2)=10,998.
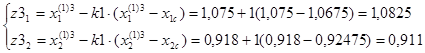
F(z3)=11,019.
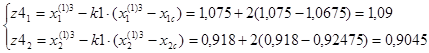
F(z3)=11,062.
Значение функции в точке z1 меньше, значения функции в точке 3, поэтому принимаем новый симплекс (1,2,z1).
,
.
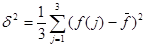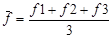В результате получаем x1=-0,012, x2=0,419, f(x1, x2)=-0,014.
Метод покоординатного спуска
(1,065; 0,918).
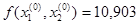
α=5ε=0,005.
Шаг 1
Координату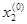 
закрепляем,
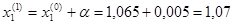
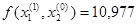
Т.к.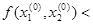 
,
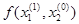Следовательно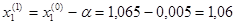 
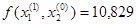
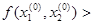
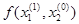
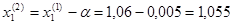
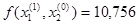
Получим x1=0,012,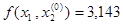 
Шаг 2
Принимаем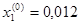 
и закрепляем,
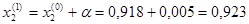
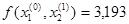
Т.к.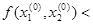 
,
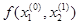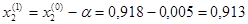
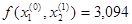
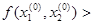
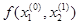
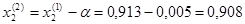
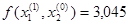
Получим x2=0,199,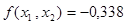 
Продолжаем поиск до тех пор, пока не будет выполнено условие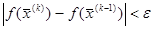 
В результате получаем x1=0,117, x2=0,189, f(x1, x2)=-0,411.
Метод Хука-Дживса
x0: (1,065; 0,918).
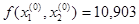
Δ1=5*ε=5*0,001, Δ2=5*ε=5*0,001.
λ=2.
Шаг 1
Принимаем k1=-1, k2=-1 – коэффициенты, определяющие направление поиска.
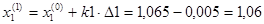
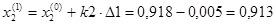
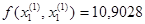
В данном направлении функция убывает.
Шаг 2
Принимаем k1=-1, k2=-1.
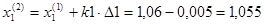
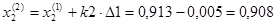
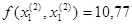
В данном направлении функция убывает.
Продолжаем поиск до тех пор, пока не будет выполнено условие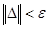 
В результате получаем x1=0,115, x2=0,198, f(x1, x2)=-0,411.
Дата: 2019-05-29, просмотров: 218.
