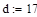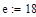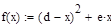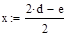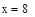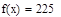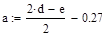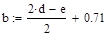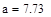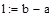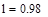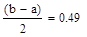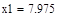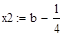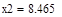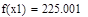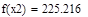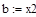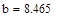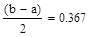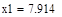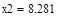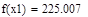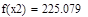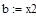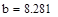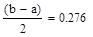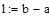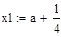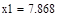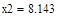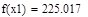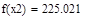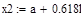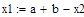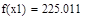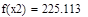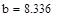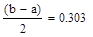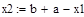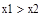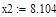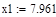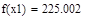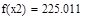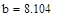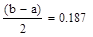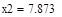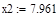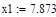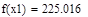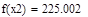Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине «Теория принятия решений»

 

Тема: «Сравнительный анализ методов оптимизации»

 

 

Караганда 2009

Введение

 

Необходимо выполнить оптимизацию заданных целевых функций. Определить параметры заданного геометрического тела методом многопараметрической оптимизации. В процессе решения задач оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум).

Актуальность математического моделирования процессов и явлений заключается в том, что функции и методы их оптимизации, которые исследуется в данном курсовом проекте, довольно часто применяется на практике в различных сферах жизнедеятельности, и их исследование позволило бы сократить временные и материальные затраты предприятий, использующих в производстве данные математические модели.

 

Основы теории оптимизации

Оптимизация – это выбор наилучшего решения. Математическая теория оптимизации включает в себя фундаментальные результаты и численные методы, позволяющие находить наилучший вариант из множества возможных альтернатив без их полного перебора и сравнения.

Для того чтобы использовать результаты и вычислительные процедуры теории оптимизации на практике, необходимо, прежде всего, сформулировать рассматриваемую задачу на математическом языке, т.е. построить математическую модель объекта оптимизации.

Построение математических моделей оптимизации можно условно разбить на следующие основные этапы.

1. Определение границ объекта оптимизации. Необходимость этого этапа диктуется невозможностью учета и исчерпывающего описания всех сторон большинства реальных систем. Выделив главные переменные, параметры и ограничения, следует приближенно представить систему как некоторую изолированную часть реального мира и упростить ее внутреннюю структуру. Может оказаться, что первоначальные границы объекта оптимизации выбраны неудачно. Тогда в одних случаях границы системы следует расширить, а в других – сузить.

2. Выбор управляемых переменных. На этом этапе математического моделирования необходимо провести различие между теми величинами, значения которых можно варьировать и выбирать с целью достижения наилучшего результата (управляемыми переменными), и величинами, которые фиксированы или определяются внешними факторами. Определение тех значений управляемых переменных, которым соответствует наилучшая (оптимальная) ситуация, и представляет собой задачу оптимизации.

3. Формулировка математической задачи оптимизации. Объединяя результаты предыдущих этапов построения математической модели, ее записывают в виде математической задачи оптимизации, включающей построенную целевую функцию и найденные ограничения на управляемые переменные. При записи математических задач оптимизации в общем виде обычно используется следующая символика:

 

f(x_i) ®min (max), х_iÎ U

 

где f(x_i) – целевая функция, а U – допустимое множество, заданное ограничениями на управляемые переменные. Значение параметров f(x_i) ®min (max) при которых достигается min (max), называется оптимальным решением.

 

Метод дихотомии

 

В этом методе точки x₁ и х₂ располагаются близко к середине очередного отрезка [а; b], т.е:

 ,

 

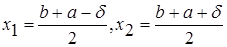где d > 0 – малое число. При этом отношение длин нового и исходного отрезков 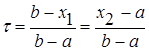 близко к 1/2, этим и объясняется название метода.

Отметим, что для любых точек x₁ и х₂ величина t > 1/2, поэтому указанный выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска х*.

В конце вычислений по методу дихотомии в качестве приближенного значения х* берут середину последнего из найденных отрезков [а; b], убедившись предварительно, что достигнуто неравенство .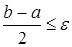

Опишем алгоритм метода деления отрезка пополам.

Шаг 1. Определить x₁ и х₂ по формулам (2.11). Вычислить f (x₁) и f (x₂).

Шаг 2. Сравнить f (x₁) и f (x₂). Если 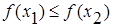, то перейти к отрезку [а; x₂], положив b = x₂ , иначе – к отрезку [x₁; b], положив а = x₁ .

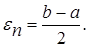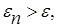Шаг 3. Найти достигнутую точность  Если , то перейти к следующей итерации, вернувшись к шагу 1. Если 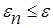, то завершить поиск х*

 

Метод золотого сечения

 

Рассмотрим такое симметричное расположение точек x₁ и х₂ на отрезке [а; b], при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения f (x), так как другое значение уже найдено на одной из предыдущих итераций.

Рассмотрим сначала отрезок [0; 1] и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть х₂ = t, тогда симметрично расположенная точка х₁ = 1–t (рис.2.2).

 

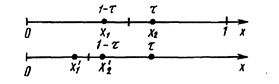
Рис. 2.2.-Определение пробных точек в методе золотого сечения

Пробная точка х₁ отрезка [0; 1] перейдет в пробную точку х₂¢ = 1–t нового отрезка [0; т]. Чтобы точки х₂ = t, и х₂¢ = 1–t делили отрезки [0; 1] и [0; t] в одном и том же отношении, должно выполняться равенство 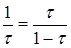 или 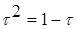, откуда находим положительное значение 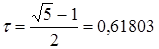… Таким образом, х₁ = 1–t = , .

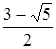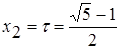Для произвольного отрезка [а; b] выражения для пробных точек примут вид

 

; .

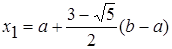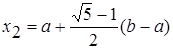1. Точки x₁ и х₂ обладают следующим свойством: каждая из них делит отрезок [а; b] на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей частей отрезка. Точки с таким свойством называются точками золотого сечения отрезка [а; b].

2. На каждой итерации исключения отрезков с пробными точками одна из них  переходит на следующий отрезок и значение f (x) в этой точке вычислять не следует. Если новым отрезком становится [а; х₂], то на него переходит пробная точка 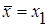 исходного отрезка, становясь его второй пробной точкой (х₂^’= х₁) (рис. 2.2). В случае перехода к отрезку [х₁; b] пробная точка  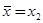исходного отрезка становится первой пробной точкой отрезка [х₁; b].

3. Легко проверить, что х₁=а+ b –х₂ , и x₂=а+ b –х₁. Поэтому на каждой итерации метода золотого сечения недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке с помощью сложения и вычитания.

4. В конце вычислений по методу золотого сечения в качестве приближенного значения х* можно взять середину последнего из полученных отрезков .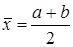

На каждой итерации отрезок поиска точки минимума уменьшается в одном и том же отношении 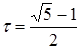, поэтому в результате п итераций его длина становится 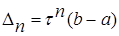. Таким образом, точность e_n определения точки х* после п итераций находят из равенства , а условием окончания поиска точки х* с точностью e служит неравенство e_n £ e.

Пример решения методами дихотомии и золотого сечения

 

Дана функция 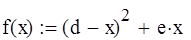, где d=2, e=1

Необходимо найти минимум на отрезке [a,b], где 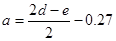, , т.е. на отрезке [7.23,8.21]

Составить программу, которая выдаст число итераций при точности ε=0,001

Решить двумя методами: дихотомии и золотого сечения

 

Решение методом дихотомии:

 

 

Шаг 1:

 

 

 

 

 

 

Шаг 2:

 

Так как f1<f2

 

 

 

 

 

 

 

 

 

 

 

Шаг 3:

Так как f1<f2

 

 

 

 

 

 

 

 

 

Решение методом золотого сечения:

 

Шаг 1:

Шаг 2:

Так как f1<f2

Шаг 3:

Так как f1<f2

 

Так как f1<f2

Листинг программы реализующей методы дихотомии и золотого сечения представлен в приложении А

 

Пример решения методами правильного симплекса, деформируемого симплекса, покоординатного спуска, Хука – Дживса

Дана функция 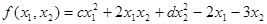, с=7; d=7.

Найти минимум функции с точностью ε=0,001

Метод правильного симплекса

Выбираем длину стороны треугольника l=10ε=0,0001

Вершины треугольника находим следующим образом:

 

A( );

B( );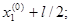

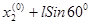D( ).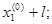

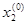A(1,065; 0,918);

B(1,07,0,927);

D(1,075,0,918).

 

Шаг 0

 

F(A)=10,903; F(B)=11,081; F(D)=11,051.

F1<F2<F3:

F1=F(A); F2=F(D); F3=F(B).

 

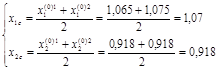
Отражаем вершину 3 относительно центра тяжести.

 

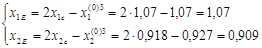
F(E)=10,873.

 

Значение функции в найденной точке меньше, значения функции в точке 1, поэтому принимаем новый симплекс (1,2,E).

Шаг 1

F(1)=10,903; F(2)=11,081; F(E)=10,873.

F1<F2<F3:

F1=F(E); F2=F(1); F3=F(2).

 

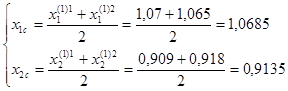
Отражаем вершину 3 относительно центра тяжести.

 

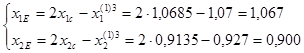
F(E)=10,726.

 

Значение функции в найденной точке меньше, значения функции в точке 1, поэтому принимаем новый симплекс (1,2,E).

 

,

.

 

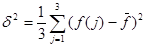В результате получаем x₁=0,125, x₂=0,208, f(x₁, x₂)=-0,41.

Метод деформируемого симплекса

Выбираем длину стороны треугольника l=5ε=0,005

Вершины треугольника находим следующим образом:

 

A( );

B( );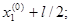

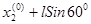D( ).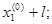

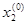A(1,065; 0,918);

B(1,07,0,927);

D(1,075,0,918).

 

Принимаем коэффициенты выбора пробных точек k1=0,5, k2=1, k3=2.

Шаг 0

 

F(A)=10,903; F(B)=11,081; F(D)=11,051.

F1<F2<F3:

F1=F(A); F2=F(D); F3=F(B).

 

Находим центр тяжести вершины 3 относительно вершин 1 и 2:

 

 

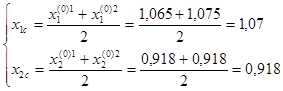
Выбираем пробные точки:

 

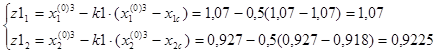
F(z1)=10,966.

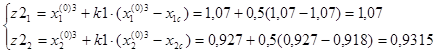
F(z2)=11,018.

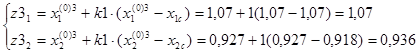
F(z3)=11,044.

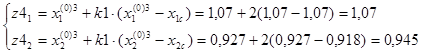
F(z3)=11,097.

Значение функции в z1 точке меньше, значения функции в точке 3, поэтому принимаем новый симплекс (1,2,z1).

Шаг 1

 

F(1)= 10,903; F(2)= 11,051; F(z1)=10,966.

F1<F2<F3:

F1=F(1); F2=F(z1); F3=F(2).

 

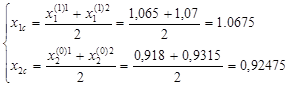
Выбираем пробные точки:

 

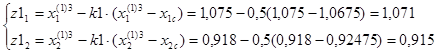
F(z1)=10,955.

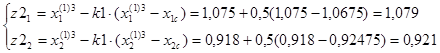
F(z2)=10,998.

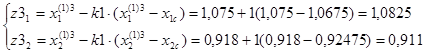
F(z3)=11,019.

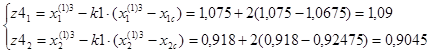
F(z3)=11,062.

Значение функции в точке z1 меньше, значения функции в точке 3, поэтому принимаем новый симплекс (1,2,z1).

 

,

.

 

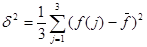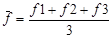В результате получаем x₁=-0,012, x₂=0,419, f(x₁, x₂)=-0,014.

Метод покоординатного спуска

 

(1,065; 0,918).

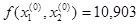
α=5ε=0,005.

 

Шаг 1

Координату 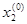 закрепляем,

 

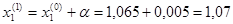
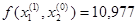
Т.к. ,

 

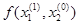Следовательно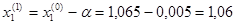

 

 

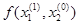
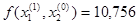
Получим x₁=0,012,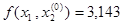

Шаг 2

Принимаем 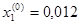 и закрепляем,

 

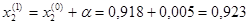
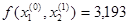
Т.к. ,

 

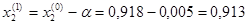
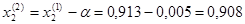
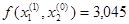
Получим x₂=0,199,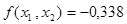

Продолжаем поиск до тех пор, пока не будет выполнено условие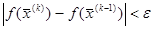

В результате получаем x₁=0,117, x₂=0,189, f(x₁, x₂)=-0,411.

Метод Хука-Дживса

 

x⁰: (1,065; 0,918).

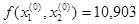
Δ1=5*ε=5*0,001, Δ2=5*ε=5*0,001.

λ=2.

 

Шаг 1

Принимаем k1=-1, k2=-1 – коэффициенты, определяющие направление поиска.

 

 

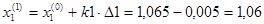
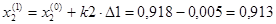
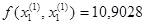
В данном направлении функция убывает.

Шаг 2

Принимаем k1=-1, k2=-1.

 

 

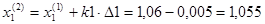
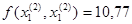
В данном направлении функция убывает.

Продолжаем поиск до тех пор, пока не будет выполнено условие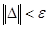

В результате получаем x₁=0,115, x₂=0,198, f(x₁, x₂)=-0,411.

 

Пример решения задач ЛП симплекс – методом

 

Дана функция  и ограничения

 

 

a=3, b=6, c=4, k подобрать таким образом, чтобы область была пятиугольной.

Заключение

В ходе выполнения данной курсовой работы нам удалось решить следующие задачи:

1. проведен анализ методов однопараметрический безусловной оптимизации;

2. проведен анализ методов многопараметрический безусловной оптимизации;

3. были разобраны основы линейного программирования;

4. был смоделирован и оптимизирован трёхмерный объект;

 

Список использованной литературы

1. Дегтярев Ю.И., «Исследование операций», Москва 1986;

2. Турчак Л.И., «Основы численных методов», Москва 1987;

3. Мудров А.Е., «Численные методы», Томск 1991;

4. Щетинин Е.Ю., «Математические методы оптимизации»;

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине «Теория принятия решений»

 

Тема: «Сравнительный анализ методов оптимизации»

 

 

Караганда 2009

Введение

 

Необходимо выполнить оптимизацию заданных целевых функций. Определить параметры заданного геометрического тела методом многопараметрической оптимизации. В процессе решения задач оптимизации должны быть найдены такие значения проектных параметров, при которых целевая функция имеет минимум (или максимум).

Актуальность математического моделирования процессов и явлений заключается в том, что функции и методы их оптимизации, которые исследуется в данном курсовом проекте, довольно часто применяется на практике в различных сферах жизнедеятельности, и их исследование позволило бы сократить временные и материальные затраты предприятий, использующих в производстве данные математические модели.

 

Основы теории оптимизации

Оптимизация – это выбор наилучшего решения. Математическая теория оптимизации включает в себя фундаментальные результаты и численные методы, позволяющие находить наилучший вариант из множества возможных альтернатив без их полного перебора и сравнения.

Для того чтобы использовать результаты и вычислительные процедуры теории оптимизации на практике, необходимо, прежде всего, сформулировать рассматриваемую задачу на математическом языке, т.е. построить математическую модель объекта оптимизации.

Построение математических моделей оптимизации можно условно разбить на следующие основные этапы.

1. Определение границ объекта оптимизации. Необходимость этого этапа диктуется невозможностью учета и исчерпывающего описания всех сторон большинства реальных систем. Выделив главные переменные, параметры и ограничения, следует приближенно представить систему как некоторую изолированную часть реального мира и упростить ее внутреннюю структуру. Может оказаться, что первоначальные границы объекта оптимизации выбраны неудачно. Тогда в одних случаях границы системы следует расширить, а в других – сузить.

2. Выбор управляемых переменных. На этом этапе математического моделирования необходимо провести различие между теми величинами, значения которых можно варьировать и выбирать с целью достижения наилучшего результата (управляемыми переменными), и величинами, которые фиксированы или определяются внешними факторами. Определение тех значений управляемых переменных, которым соответствует наилучшая (оптимальная) ситуация, и представляет собой задачу оптимизации.

3. Формулировка математической задачи оптимизации. Объединяя результаты предыдущих этапов построения математической модели, ее записывают в виде математической задачи оптимизации, включающей построенную целевую функцию и найденные ограничения на управляемые переменные. При записи математических задач оптимизации в общем виде обычно используется следующая символика:

 

f(x_i) ®min (max), х_iÎ U

 

где f(x_i) – целевая функция, а U – допустимое множество, заданное ограничениями на управляемые переменные. Значение параметров f(x_i) ®min (max) при которых достигается min (max), называется оптимальным решением.