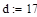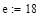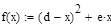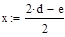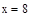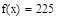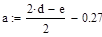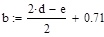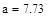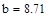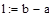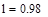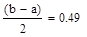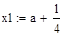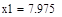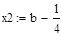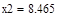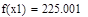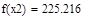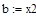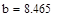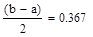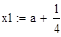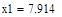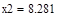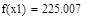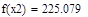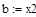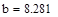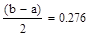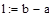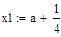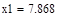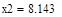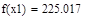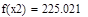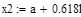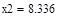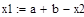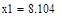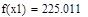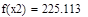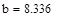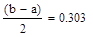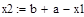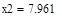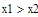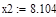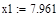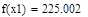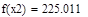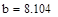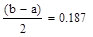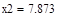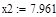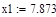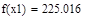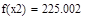Число х* Î U называется точкой глобального (абсолютного) минимума функции f (x) на множестве U, если f (x*) £ f (x) для всех хÎ U.
Значение f * = f (x*) =  называют глобальным (абсолютным) минимумом или просто минимумом функции f (x) на множестве U.
называют глобальным (абсолютным) минимумом или просто минимумом функции f (x) на множестве U.
Множество всех точек минимума f (x) на U будем в дальнейшем обозначать через U*.
Число 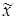 ÎU называется точкой локального минимума функции f (x), если
ÎU называется точкой локального минимума функции f (x), если 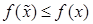 для всех xÎU, достаточно близких к
для всех xÎU, достаточно близких к  , т.е. если существует e > 0 такое, что это неравенство выполняется для любого
, т.е. если существует e > 0 такое, что это неравенство выполняется для любого 
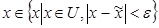 .
.
Глобальный минимум f (x) является и локальным минимумом, а обратное, неверно.
Если функция f ( x ) на множестве U имеет, кроме глобального, локальные минимумы, отличные от него, то минимизация f ( x ), как правило, сильно затрудняется. В частности, многие методы поиска точки минимума f ( x ) приспособлены только для функций, у которых каждый локальный минимум является одновременно и глобальным. Этим свойством обладают унимодальные функции.
Функция f ( x ) называется унимодальной на отрезке [а; b], если она непрерывна на [а; b] и существуют числа a и b, 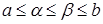 , такие, что:
, такие, что:
1) если а < a, то на отрезке [a; a] функция f ( x ) монотонно убывает;
2) если b < b, то на отрезке [b; b] функция f ( x ) монотонно возрастает;
3) при х Î [a; b] f ( x ) =f * = 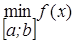 .
.
Возможно вырождение в точку одного или двух отрезков из [a; a], [a; b] и [b; b]. Некоторые варианты расположения и вырождения в точку отрезков монотонности и постоянства унимодальной функции показаны на.
Основные свойства унимодальных функций:
1. Любая из точек локального минимума унимодальной функции является и точкой ее глобального минимума на отрезке [а; b].
2. Функция, унимодальная на отрезке [а; b], является унимодальной и на любом меньшем отрезке [с; d] 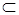 [а; b].
[а; b].
3. Пусть f (x) 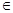 Q [а; b] и
Q [а; b] и 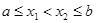 . Тогда:
. Тогда:
если 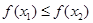 , то x*
, то x* 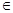 [a; x2];
[a; x2];
если 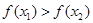 , то x*
, то x* 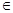 [x1; b],
[x1; b],
где х* – одна из точек минимума f (x) на отрезке [a; b].
Из численных методов одномерной безусловной оптимизации рассмотрим два:
1. метод дихотомии
2. метод золотого сечения
Метод дихотомии
В этом методе точки x1 и х2 располагаются близко к середине очередного отрезка [а; b], т.е:
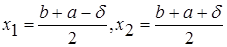 ,
,
где d > 0 – малое число. При этом отношение длин нового и исходного отрезков 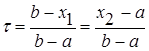 близко к 1/2, этим и объясняется название метода.
близко к 1/2, этим и объясняется название метода.
Отметим, что для любых точек x1 и х2 величина t > 1/2, поэтому указанный выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска х*.
В конце вычислений по методу дихотомии в качестве приближенного значения х* берут середину последнего из найденных отрезков [а; b], убедившись предварительно, что достигнуто неравенство 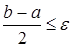 .
.
Опишем алгоритм метода деления отрезка пополам.
Шаг 1. Определить x1 и х2 по формулам (2.11). Вычислить f (x1) и f (x2).
Шаг 2. Сравнить f (x1) и f (x2). Если 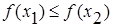 , то перейти к отрезку [а; x2], положив b = x2 , иначе – к отрезку [x1; b], положив а = x1 .
, то перейти к отрезку [а; x2], положив b = x2 , иначе – к отрезку [x1; b], положив а = x1 .
Шаг 3. Найти достигнутую точность 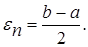 Если
Если 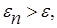 , то перейти к следующей итерации, вернувшись к шагу 1. Если
, то перейти к следующей итерации, вернувшись к шагу 1. Если 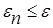 , то завершить поиск х*
, то завершить поиск х*
Метод золотого сечения
Рассмотрим такое симметричное расположение точек x1 и х2 на отрезке [а; b], при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения f (x), так как другое значение уже найдено на одной из предыдущих итераций.
Рассмотрим сначала отрезок [0; 1] и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть х2 = t, тогда симметрично расположенная точка х1 = 1–t (рис.2.2).
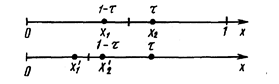
Рис. 2.2.-Определение пробных точек в методе золотого сечения
Пробная точка х1 отрезка [0; 1] перейдет в пробную точку х2¢ = 1–t нового отрезка [0; т]. Чтобы точки х2 = t, и х2¢ = 1–t делили отрезки [0; 1] и [0; t] в одном и том же отношении, должно выполняться равенство 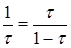 или
или 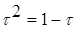 , откуда находим положительное значение
, откуда находим положительное значение 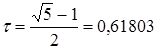 … Таким образом, х1 = 1–t =
… Таким образом, х1 = 1–t = 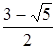 ,
, 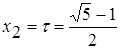 .
.
Для произвольного отрезка [а; b] выражения для пробных точек примут вид
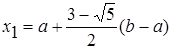 ;
; 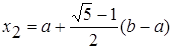 .
.
1. Точки x1 и х2 обладают следующим свойством: каждая из них делит отрезок [а; b] на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей частей отрезка. Точки с таким свойством называются точками золотого сечения отрезка [а; b].
2. На каждой итерации исключения отрезков с пробными точками одна из них 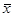 переходит на следующий отрезок и значение f (x) в этой точке вычислять не следует. Если новым отрезком становится [а; х2], то на него переходит пробная точка
переходит на следующий отрезок и значение f (x) в этой точке вычислять не следует. Если новым отрезком становится [а; х2], то на него переходит пробная точка 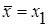 исходного отрезка, становясь его второй пробной точкой (х2’= х1) (рис. 2.2). В случае перехода к отрезку [х1; b] пробная точка
исходного отрезка, становясь его второй пробной точкой (х2’= х1) (рис. 2.2). В случае перехода к отрезку [х1; b] пробная точка 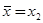 исходного отрезка становится первой пробной точкой отрезка [х1; b].
исходного отрезка становится первой пробной точкой отрезка [х1; b].
3. Легко проверить, что х1=а+ b –х2 , и x2=а+ b –х1. Поэтому на каждой итерации метода золотого сечения недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке с помощью сложения и вычитания.
4. В конце вычислений по методу золотого сечения в качестве приближенного значения х* можно взять середину последнего из полученных отрезков 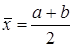 .
.
На каждой итерации отрезок поиска точки минимума уменьшается в одном и том же отношении 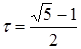 , поэтому в результате п итераций его длина становится
, поэтому в результате п итераций его длина становится 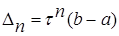 . Таким образом, точность en определения точки х* после п итераций находят из равенства
. Таким образом, точность en определения точки х* после п итераций находят из равенства 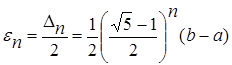 , а условием окончания поиска точки х* с точностью e служит неравенство en £ e.
, а условием окончания поиска точки х* с точностью e служит неравенство en £ e.
Пример решения методами дихотомии и золотого сечения
Дана функция 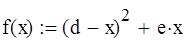 , где d=2, e=1
, где d=2, e=1
Необходимо найти минимум на отрезке [a,b], где 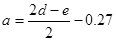 ,
, 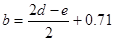 , т.е. на отрезке [7.23,8.21]
, т.е. на отрезке [7.23,8.21]
Составить программу, которая выдаст число итераций при точности ε=0,001
Решить двумя методами: дихотомии и золотого сечения
Решение методом дихотомии:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Шаг 1: |
|
|
|
|
|
|
|
|
|
|
|
|
| Шаг 2: |
| Так как f1<f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Шаг 3: |
| Так как f1<f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение методом золотого сечения:
| Шаг 1: |
|
|
|
|
|
|
|
|
|
|
|
|
| Шаг 2: |
| Так как f1<f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Шаг 3: |
| Так как f1<f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как f1<f2
Листинг программы реализующей методы дихотомии и золотого сечения представлен в приложении А
Дата: 2019-05-29, просмотров: 356.