Теоретическую линию зацепления N1 N2 делим на равные отрезки. По формулам (3.32) и (3.33)определяем величины коэффициентов l1, l2 и сводим в таблицу.
 l1=
l1= 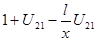 (3.22)
(3.22)
l2= 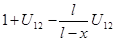 (3.21)
(3.21)
U21=Z1/Z2=15/30=0,5;
U12=Z2/Z1=30/15=2.
Таблица 8. Значение коэффициентов  l1 и l2.
l1 и l2.
| X | 0 | 24 | 48 | 72 | 96 | 120 | 144 | 168 | 192 | 216 | 240 |
| l1 | -¥ | -3,50 | -1,00 | -0,17 | 0,25 | 0,5 | 0,67 | 0,79 | 0,88 | 0,94 | 1 |
| l2 | 1 | 0,78 | 0,5 | 0,14 | -0,33 | -1,0 | -2,00 | -3,67 | -7,00 | -17 | -¥ |
По полученным значениям коэффициентов удельных скольжений строим графики.
4. Синтез кулачкового механизма
4.1 Задание
4.1.1 Для построения профиля кулачка достаточно иметь зависимость S= S(j). Для этого дважды проинтегрируем зависимость 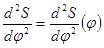 .
.
Для получения наглядного результата целесообразно применить метод графического интегрирования зависимости 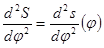 и
и 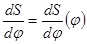 .
.
Заменяя график 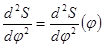 ступенчатым, по принципу равенства прибавляемых и вычитаемых площадок с целью выполнения операции графического интегрирования. В результате интегрирования получаем график
ступенчатым, по принципу равенства прибавляемых и вычитаемых площадок с целью выполнения операции графического интегрирования. В результате интегрирования получаем график 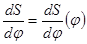 .
.
Интегрируя тем же способом график 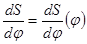 , получаем график
, получаем график 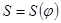 .
. 
Определим масштабные коэффициенты для графиков.
Масштаб углов поворота:
mj= 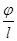 ; (4.1)
; (4.1)
где: j = jп:
j =60о:
mj==0.25 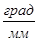 =0.00436
=0.00436 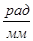
Таблица 9. Значения hS и S,Ls.
| Отрезок | hS, мм 
| S,мм | Ls,мм |
| 0 | 0 | 0 | 0 |
| 1 | 13 | 1 | 3 |
| 2 | 46 | 5 | 15 |
| 3 | 91 | 10 | 30 |
| 4 | 136 | 15 | 45 |
| 5 | 170 | 19 | 57 |
| 6 | 183 | 20 | 60 |
Введём масштабный коэффициентграфиков.
mS=0.109(м/мм); (4.2)
mS= 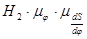 (4.3)
(4.3)
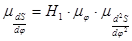 (4.4)
(4.4)
где: Н1,Н2-полюсные расстояния, мм;
Н1=70
Н2=80(мм).
Из 4.3 получаем:
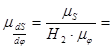
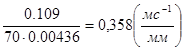 .
.
Из 4.4 будем иметь:
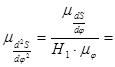
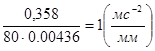 .
.
4.2.2 Задачей динамического синтеза является определение такого минимального радиуса-вектора Rmin профиля кулачка и такого расстояния d между центрами вращения кулачка и толкателя при наличии которых переменный угол передачи движения ни в одном положении кулачкового механизма не будет меньше gmin
Графическое построение для определения минимального радиуса кулачка будем проводить в масштабе mS. Чтобы определить минимальный радиус кулачка нам нужно построить графики зависимости S-dS/dj. Для этого выберем масштабный коэффициент mS=0,333.
Для определения S и dS/dj воспользуемся формулами:
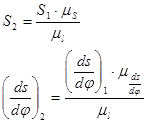 (4.5)
(4.5)
где: S2,S1-расстояния на диаграмме S-dS/dj и S-j соответственно, мм.
(ds/dj)2,(ds/dj)1 – значение скорости на диаграмме S-ds/dj и ds/dj -j, соответственно.
Точка В - центр вращения толкателя. Дуга радиуса lявляется ходом толкателя h= l Sмах. Эта дуга размечена в соответствии с осью ординат диаграммы y-S.
Полученные значения заносим в таблицу- 10
Таблица 10.
| отрезок | hdy/dj, мм | ds/dj, мм | l(ds/dj)мм |
| 0 | 0 | 0 | 0 |
| 1 | 42 | 15 | 45 |
| 2 | 72 | 26 | 78 |
| 3 | 84 | 30 | 90 |
| 4 | 72 | 26 | 78 |
| 5 | 42 | 15 | 45 |
| 6 | 0 | 0 | 0 |
Направление отрезков определяется поворотом вектора скорости точки А толкателя на 90о в сторону вращения кулачка. Через концы этих отрезков проводим прямые образующие с соответствующими лучами углы gmin.
gmin>gдоп; (4.6)
gmin=90о-gдоп
gmin=90о-30о=60о
60о>30о
Rmin=0,042 (м);
4.2.3 Предполагаем, что кулачок вращается противоположно вращению часовой стрелки. Все построения ведём в масштабе:
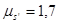
Для получения практического профиля кулачка нужно построить огибающую дугу радиуса r ролика, имеющих центры на теоретическом профиле.
Для устранения самопересечения профиля кулачка, а также из конструктивных соображений длина r радиуса ролика должна удовлетворять условию:
r <(0.4¸0.5)r0; (4.7)
где: r0 – минимальный радиус кулачка,r0=0.042(м).
0,042×0,4>0.014;
Принимаем радиус ролика r=0.014(м)=14(мм).
Дата: 2019-05-29, просмотров: 337.