Задание
Таблица 1-Исходные данные
| Параметры | Обозначения | Единица | Значение | |||
| 1. | Размеры звеньев рычажного механизма LAS2=0.5LAB LBS4=0.5LBC | LO1A LAB LBC L1 L2 LВО2 | м м м м м м | 0.27 2.23 0,95 0,06 0,07 0,27 | ||
| 2 | Частота вращения электродвигателя | nдв | об/мин | 720 | ||
| 3. | Частота вращения кривошипа и кулачка. | N1=nk | об/мин | 62 | ||
| 4. | Массы звеньев | m2 m3 m4 m5 | кг кг кг кг | 0,35 0,10 0,4 1,05 | ||
| 5. | Момент инерции звеньев | Js2 Js3 Js4 Jдв | кг.м2 кг.м2 кг.м2 кг.м2 | 0.041 0.0016 0.026 0.02 | ||
| 6 | Максимальная сила сопротивления | F | kH | 3,5 | ||
| 7. | Коэффициент неравномерности вращения кривошипа. | d | - | 1/8 | ||
| 8. | Положение кривошипа1 при силовом расчёте. | j1 | град | 150 | ||
| 9. | Модуль зубьев колёс планетарного редуктора | m1 | мм | 3 | ||
| 10. | Числа зубьев колёс передачи равносмещённого зацепления | ZA ZB | - - | 15 30 | ||
| 11. | Модуль зубчатых колёсZA и ZB | m | мм | 6 | ||
| 12. | Ход толкателя кулачкового механизма | h | мм | 20 | ||
| 13. | Фазовые углы поворота кулачка | jBB jn=j0 | град град | 130 60 | ||
| 14. | Допускаемый угол давления | Vдоп | град | 30 | ||
Введение
Курс теории механизмов и машин рассматривает общие методы исследования и проектирования и является общетехнической дисциплиной, формирует знание инженеров по конструированию, изготовлению и эксплуатации машин. Общие методы синтеза механизмов позволяют будущему инженеру определять многие параметры проектируемых механизмов и машин. Даёт основы для подготовки инженеров-механиков по технологии изготовления и эксплуатации машин. Знание видов механизмов, их кинематических и динамических свойств, методов их синтеза, даёт возможность инженеру ориентироваться не только в принципах работы, но и в их технологической взаимосвязи на производстве. Курс теории механизмов и машин является основой для изучения последующих дисциплин.
Курсовое проектирование по теории механизмов и машин является самостоятельной творческой работой студентов. В процессе разработки курсового проекта студент должен решить ряд расчётно-графических задач, с решением которых инженеру-конструктору приходится встречаться на современном производстве. Цель курсового проекта - развить у студентов навыки самостоятельного решения комплексных инженерных задач, приобретение навыков оформление конструкторской документации в соответствии с требованиями ЕСКД.
1.1 Построение плана механизма
План механизма строим для тринадцати положений. Построение начнём с выбора длины отрезка кривошипа (54мм), обозначим через О1А длину отрезка кривошипа в миллиметрах а через lO1A - истинную длину кривошипа в метрах, составив отношение истинной длины к длине отрезка получим значение масштабного коэффициента.
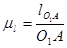 (1.1)
(1.1)
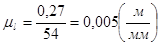
По значению ml находим :длины отрезков остальных звеньев механизма в миллиметрах. Для этого истинные длины звеньев в метрах делим на масштаб ml.
Отрезком О1А, как радиусом, изображаем окружность с центром в точке О1.
Путем вращения О1А отрезка находим два крайних (мертвых) положения механизма. В мертвых положениях кривошип и примыкающий к нему шатун находятся на одной линии.
После нахождения мертвых положений механизма и определения направления вращения кривошипа строим плана механизма.
За исходное нулевое выбираем первое мертвое положение механизма. Последующие положения строим через 30° поворота кривошипа.
1.2 Построение плана аналогов скоростей
Определим скорость точки А. Зная частоту вращения кривошипа О1А и его длину, определим скорость точки А, используя формулу:
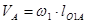 (1.2)
(1.2)
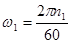 (1.3)
(1.3)
где n1 – частота вращения кривошипа.
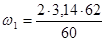 =6,5 (рад/с)
=6,5 (рад/с)
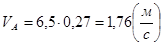
Скорость точки А во всех положениях механизма постоянна, и графически выражается вектором ра.
Определим масштабный коэффициент плана скоростей.
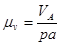 (1.4)
(1.4)
где ра – отрезок на плане скоростей определяющий скорость точки А, мм.

Определим скорость точки В. Для этого рассмотрим её движение относительно точек А и О2 . Получаем систему уравнений.
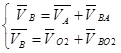 (1.5)
(1.5)
где: VA - скорость точки А.
VBA – скорость точки В относительно точки А.
VВО2 – скорость точки В относительно точки О2.
VО2 – скорость точки О2, равна, 0 т.к. данная точка неподвижна.
Решая графическим методом систему уравнений (5), получим скорость точки В, которая графически выражается вектором рв.
Для определения скорости точки С, рассмотрим её движение относительно точек В и Сх . Получаем систему уравнений.
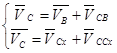 (1.6)
(1.6)
где: VВ - скорость точки В.
VСВ – скорость точки С относительно точки В.
VССх – скорость точки С относительно точки Сх.
VСх – скорость точки К, равна, 0 т.к. данная точка неподвижна.
Решая графическим методом систему уравнений (1.6), получим скорость точки С, которая графически выражается вектором рс.
Отрезок рs2 скорости точки S2 находим по принципу подобия.. Длину отрезка ps2 определяем из пропорции.
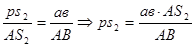 (1.7)
(1.7)
Аналогично находим скорость точки ps4
 (1.8)
(1.8)
Значения аналогов скоростей рs2 , ps4 , заносим в таблицу 2.
Таблица 2. Значения аналогов скоростей рs2 , ps4.
| Положение механизма. | 1 | 2 | 3 | 4 | 5 | 6 | 6’ | 7 | 8 | 9 | 10 | 11 |
| ps2 | 75 | 71 | 70 | 76 | 90 | 110 | 0 | 110 | 103 | 98 | 93 | 84 |
| ps4 | 42 | 49 | 62 | 93 | 117 | 81 | 0 | 106 | 118 | 96 | 68 | 47 |
Силовой анализ механизма
Силовое исследование механизма проводим в порядке обратном структурному. Исследование будем проводить без учёта сил трения в кинематических парах. Силы тяжести прикладываем к центру масс.
К диаде (2,3) и (4,5) приложим все силы и момент сил, действующие на неё. Сила сопротивления задана графиком и имеет направление, противоположное рабочему ходу исполнительного органа Величину сил инерции определим по формулам:
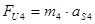 (2.9)
(2.9)
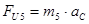 (2.10)
(2.10)
где: m4 и m5 – массы звеньев 4и5 (кг)
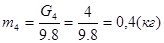
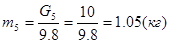
аS4 и (aС=aS5)– ускорение центров масс звеньев (м/с2).
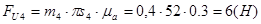
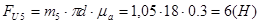
Кроме того на звено 4 действует момент пары сил инерции который имеет направление, противоположно угловому ускорению звена. Его величину определим по формуле:
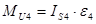 (2.11)
(2.11)
где: IS4 – осевой момент инерции звена, кг×м2; e4 – угловое ускорение звена, рад/с2.
 (2,12)
(2,12)
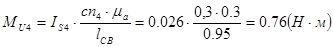
Для определения силы Ft43 составим условие моментного равновесия звена 4.
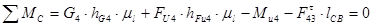 (2.13)
(2.13)
Из уравнения (2.13) будем иметь:
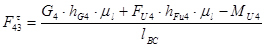 (2.14)
(2.14)
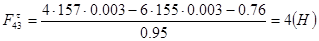
Для определения F50 и Fn43 составим векторное уравнение и строим план сил. Уравнение записываем таким образом чтобы неизвестные реакции стояли по краям уравнения. Для удобства сначала записываем силы, действующие на одно звено, а затем все силы, действующие на другое.
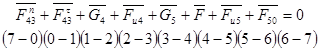 (2.15)
(2.15)
Введём масштабный коэффициент плана сил:
 (2.16)
(2.16)
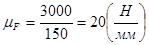
F50=520(H);
Fn43=F43=3000(H);
Рассмотрим диаду 2-3.
Определим силы инерции, действующие на звенья.
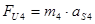 (2.17)
(2.17)
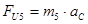 (2.18)
(2.18)
где: m2 и m3 – массы звеньев 2и3 (кг)
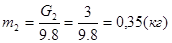
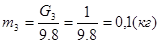
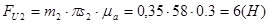
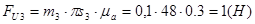
Определим момент пары сил инерции.
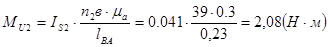
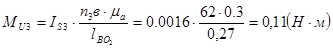
Для определения силы Ft21 составим условие моментного равновесия звена 2.
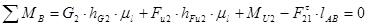 (2.19)
(2.19)
Из уравнения (2.17) будем иметь:
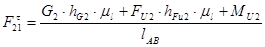 (2.20)
(2.20)
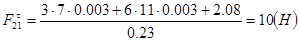
Для определения силы Ft30 составим условие моментного равновесия звена 3.
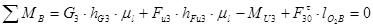 (2.21)
(2.21)
Из уравнения (2.19) будем иметь:
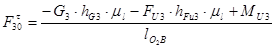 (2.22)
(2.22)
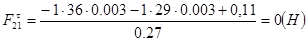
Для определения Fn30 и Fn21 составим векторное уравнение и строим план сил. Уравнение записываем таким образом чтобы неизвестные реакции стояли по краям уравнения.
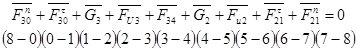 (2.23)
(2.23)
Введём масштабный коэффициент плана сил:
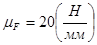
Fn30= F30=4400(H); Fn21=F21=3200(Н).
Задание
3.1.1 Модуль зубчатых колёс планетарного механизма: m1= 3 мм
Числа зубьев колёс простой передачи: Z1=15 , Z2=30;
Модуль зубчатых колёс Z1и Z2: m=6 мм;
Все зубчатые колёса должны быть нулевыми. А это значить, что во избежание подреза ножки зуба для колёс с внешним зацеплением принимают Z>17, для колёс с внутренним зацеплением Z>85.
Подберём числа зубьев Z1,Z2,Z3 для зубчатой передачи с передаточным отношением U=nдв/n1=720/62=11,6.
Задаёмся числом зубьев Z1 из ряда Z1=17,18,19,…. Пусть Z1=20. Число зубьев Z3 найдём из выражения:
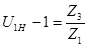 (3.1)
(3.1)
где: U1H – передаточное отношение планетарной передачи входного колеса к выходному звену (водилу) при неподвижном опорном колесе.

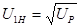 (3.2)
(3.2)
где: Uр – передаточное число одной ступени редуктора.
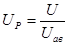 (3.3)
(3.3)
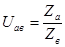 (3.4)
(3.4)
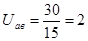
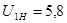
Из формулы (1.1) найдём Z3.
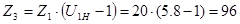
Условие Z3>Zmin=85 выполняется.
Оси центральных колёс и водила должны совпадать между собой, т.е. должно соблюдаться условие соосности, которое имеет вид:
Z1+2Z2=Z3 (3.5)
Из условия соосности находим Z2.
Z2=(Z3-Z1)/2=(96-20)/2=38
Сателлиты должны быть с таким окружным шагом, чтобы между окружностями вершин соседних сателлитов обеспечивался гарантированный зазор- условие соседства:
Sin(1800/k)>(Z2+2)/(Z1+Z2) (3.6)
где: к - число сателитов.
Из условия соседства определяем возможное число сателлитов в механизме.

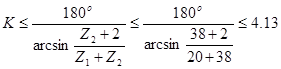
Значит, для этого механизма число сателлитов может быть взято равным 2,3 и 4. Принимаем k=4. Проверяем условие сборки.
Сборка сателлитов должна осуществляться без натягов при равных окружных шагах между ними. Это возможно при выполнении следующего условия:
где: Ц и р целые числа.
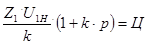 (3.7)
(3.7)
Проверку ведём при р=0.
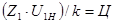
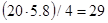
Условие сборки выполняется т.к. Ц получилось целое число.
Все условия выполняются, значит окончательно принимаем Z1=20; Z2=38; Z3=96; k=4.
Для построения кинематической схемы механизма определим радиусы делительных окружностей. 
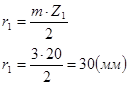
 (3.8)
(3.8)
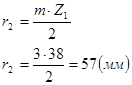 (3.9)
(3.9)
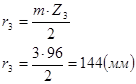 (3.10)
(3.10)
Задание
Таблица 1-Исходные данные
| Параметры | Обозначения | Единица | Значение | |||
| 1. | Размеры звеньев рычажного механизма LAS2=0.5LAB LBS4=0.5LBC | LO1A LAB LBC L1 L2 LВО2 | м м м м м м | 0.27 2.23 0,95 0,06 0,07 0,27 | ||
| 2 | Частота вращения электродвигателя | nдв | об/мин | 720 | ||
| 3. | Частота вращения кривошипа и кулачка. | N1=nk | об/мин | 62 | ||
| 4. | Массы звеньев | m2 m3 m4 m5 | кг кг кг кг | 0,35 0,10 0,4 1,05 | ||
| 5. | Момент инерции звеньев | Js2 Js3 Js4 Jдв | кг.м2 кг.м2 кг.м2 кг.м2 | 0.041 0.0016 0.026 0.02 | ||
| 6 | Максимальная сила сопротивления | F | kH | 3,5 | ||
| 7. | Коэффициент неравномерности вращения кривошипа. | d | - | 1/8 | ||
| 8. | Положение кривошипа1 при силовом расчёте. | j1 | град | 150 | ||
| 9. | Модуль зубьев колёс планетарного редуктора | m1 | мм | 3 | ||
| 10. | Числа зубьев колёс передачи равносмещённого зацепления | ZA ZB | - - | 15 30 | ||
| 11. | Модуль зубчатых колёсZA и ZB | m | мм | 6 | ||
| 12. | Ход толкателя кулачкового механизма | h | мм | 20 | ||
| 13. | Фазовые углы поворота кулачка | jBB jn=j0 | град град | 130 60 | ||
| 14. | Допускаемый угол давления | Vдоп | град | 30 | ||
Введение
Курс теории механизмов и машин рассматривает общие методы исследования и проектирования и является общетехнической дисциплиной, формирует знание инженеров по конструированию, изготовлению и эксплуатации машин. Общие методы синтеза механизмов позволяют будущему инженеру определять многие параметры проектируемых механизмов и машин. Даёт основы для подготовки инженеров-механиков по технологии изготовления и эксплуатации машин. Знание видов механизмов, их кинематических и динамических свойств, методов их синтеза, даёт возможность инженеру ориентироваться не только в принципах работы, но и в их технологической взаимосвязи на производстве. Курс теории механизмов и машин является основой для изучения последующих дисциплин.
Курсовое проектирование по теории механизмов и машин является самостоятельной творческой работой студентов. В процессе разработки курсового проекта студент должен решить ряд расчётно-графических задач, с решением которых инженеру-конструктору приходится встречаться на современном производстве. Цель курсового проекта - развить у студентов навыки самостоятельного решения комплексных инженерных задач, приобретение навыков оформление конструкторской документации в соответствии с требованиями ЕСКД.
1.1 Построение плана механизма
План механизма строим для тринадцати положений. Построение начнём с выбора длины отрезка кривошипа (54мм), обозначим через О1А длину отрезка кривошипа в миллиметрах а через lO1A - истинную длину кривошипа в метрах, составив отношение истинной длины к длине отрезка получим значение масштабного коэффициента.
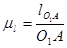 (1.1)
(1.1)
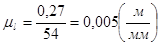
По значению ml находим :длины отрезков остальных звеньев механизма в миллиметрах. Для этого истинные длины звеньев в метрах делим на масштаб ml.
Отрезком О1А, как радиусом, изображаем окружность с центром в точке О1.
Путем вращения О1А отрезка находим два крайних (мертвых) положения механизма. В мертвых положениях кривошип и примыкающий к нему шатун находятся на одной линии.
После нахождения мертвых положений механизма и определения направления вращения кривошипа строим плана механизма.
За исходное нулевое выбираем первое мертвое положение механизма. Последующие положения строим через 30° поворота кривошипа.
1.2 Построение плана аналогов скоростей
Определим скорость точки А. Зная частоту вращения кривошипа О1А и его длину, определим скорость точки А, используя формулу:
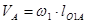 (1.2)
(1.2)
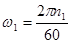 (1.3)
(1.3)
где n1 – частота вращения кривошипа.
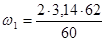 =6,5 (рад/с)
=6,5 (рад/с)
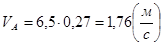
Скорость точки А во всех положениях механизма постоянна, и графически выражается вектором ра.
Определим масштабный коэффициент плана скоростей.
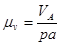 (1.4)
(1.4)
где ра – отрезок на плане скоростей определяющий скорость точки А, мм.

Определим скорость точки В. Для этого рассмотрим её движение относительно точек А и О2 . Получаем систему уравнений.
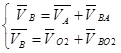 (1.5)
(1.5)
где: VA - скорость точки А.
VBA – скорость точки В относительно точки А.
VВО2 – скорость точки В относительно точки О2.
VО2 – скорость точки О2, равна, 0 т.к. данная точка неподвижна.
Решая графическим методом систему уравнений (5), получим скорость точки В, которая графически выражается вектором рв.
Для определения скорости точки С, рассмотрим её движение относительно точек В и Сх . Получаем систему уравнений.
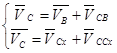 (1.6)
(1.6)
где: VВ - скорость точки В.
VСВ – скорость точки С относительно точки В.
VССх – скорость точки С относительно точки Сх.
VСх – скорость точки К, равна, 0 т.к. данная точка неподвижна.
Решая графическим методом систему уравнений (1.6), получим скорость точки С, которая графически выражается вектором рс.
Отрезок рs2 скорости точки S2 находим по принципу подобия.. Длину отрезка ps2 определяем из пропорции.
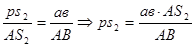 (1.7)
(1.7)
Аналогично находим скорость точки ps4
 (1.8)
(1.8)
Значения аналогов скоростей рs2 , ps4 , заносим в таблицу 2.
Таблица 2. Значения аналогов скоростей рs2 , ps4.
| Положение механизма. | 1 | 2 | 3 | 4 | 5 | 6 | 6’ | 7 | 8 | 9 | 10 | 11 |
| ps2 | 75 | 71 | 70 | 76 | 90 | 110 | 0 | 110 | 103 | 98 | 93 | 84 |
| ps4 | 42 | 49 | 62 | 93 | 117 | 81 | 0 | 106 | 118 | 96 | 68 | 47 |
Динамический анализ механизма
Дата: 2019-05-29, просмотров: 300.