Задачей силового исследования рычажного механизма является определение реакций в кинематические парах от действия заданных сил. При этом закон движения начальных звеньев является заданным. Результаты силового исследования применяются при определении: сил трения, возникающих в кинематических парах; геометрических параметров звеньев механизма; мощности, потребляемой механизмом для преодоления внешних сил.
При определении реакций в кинематических парах будем использовать принцип Даламбера, согласно которому звено механизма можно рассматривать как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции. Составим уравнения равновесия, которые называют уравнениями кинетостатики.
В результате движении механизма на его звенья действуют силы: движущие, полезных и вредных сопротивлений, тяжести звеньев, инерции звеньев. Из перечисленных сил нам заданны только силы полезных сопротивлений, а остальные подлежат определению.
Bсe силы инерция звена при его движении сведём к главному вектору сил инерции Fи, проложенному к центру масс эвена, и главному моменту Ми сил инерции.
Сила инерции имеет направление, противоположное ускорению центра масс звена. Момент пары сил инерции направлен противоположно угловому ускорению звена. Ускорения центров масс и угловые ускорения звеньев определяются с помощью планов ускорений.
Строим план механизма в масштабе:
ml=0.003(м/мм).
2.1 Построение плана скоростей
Проводим построение плана скоростей по ранее проделанной методике.
Определим скорость точки А. Зная частоту вращения кривошипа О1А и его длину, определим скорость точки А, используя формулу:
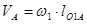 (2.1)
(2.1)
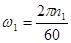 (2.2)
(2.2)
где n1 – частота вращения кривошипа.
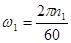 =6,5(рад/с)
=6,5(рад/с)
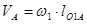 =6,5×0,27=1,76(м/с)
=6,5×0,27=1,76(м/с)
Скорость точки А во всех положениях механизма постоянна, и графически выражается вектором ра.
Определим масштабный коэффициент плана скоростей.
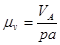 (2.3)
(2.3)
где ра – отрезок на плане скоростей определяющий скорость точки А, мм.
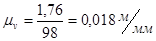
Дальнейшее построение плана скоростей проводим согласно пункта 1.2, раздела: «Динамический анализ и синтез рычажного механизма».
2.2 Построение плана ускорений
Ускорение точек звеньев механизма определяем с помощью плана ускорений. Запишем полное ускорение точки А.
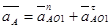 (2.4)
(2.4)
Учитывая тот факт, что кривошип вращается с постоянной угловой скоростью то его угловое ускорение аtАО1 равно 0. То есть ускорение точки А состоит только из нормального ускорения, которое направлено по звену к центру вращения кривошипа.
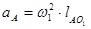 (2.5)
(2.5)
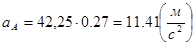
Определяем масштабный коэффициент плана ускорений.
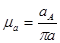 (2.6)
(2.6)
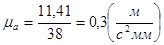
Для определения ускорения точки В, принадлежащей звену 3, воспользуемся теоремой о сложении ускорений в переносном и относительном движениях , тогда:
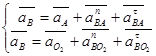 (2.7)
(2.7)
где:  - нормальное ускорение точки В относительно точки А.
- нормальное ускорение точки В относительно точки А.
 - тангенциальное ускорение точки В относительно точки А.
- тангенциальное ускорение точки В относительно точки А.
аА – ускорение точки А.
 - нормальное ускорение точки В относительно точки О2.
- нормальное ускорение точки В относительно точки О2.
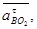 - тангенциальное ускорение точки В относительно точки О2.
- тангенциальное ускорение точки В относительно точки О2.
аО2 – ускорение точки О2, равное 0 так как точка О2 неподвижна.
Решив геометрически систему уравнений будем иметь ускорение точки В.
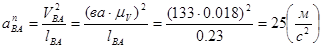
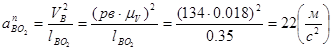
Определим ускорение точки С, для чего составим два векторных уравнения.
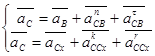 (2.8)
(2.8)
где: 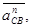 - нормальное ускорение точки С относительно точки В.
- нормальное ускорение точки С относительно точки В.
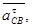 - тангенциальное ускорение точки С относительно точки D.
- тангенциальное ускорение точки С относительно точки D.
аВ – ускорение точки В.
 - кориолисово ускорение, определяется поворотом вектора относительной скорости VССx на 90о в сторону угловой скорости звена 4.
- кориолисово ускорение, определяется поворотом вектора относительной скорости VССx на 90о в сторону угловой скорости звена 4.
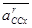
- релятивное (относительное ) ускорение точки Сx, направлено в вдоль звена 5.
Решив геометрически систему уравнений (2.8) будем иметь ускорение точки С.
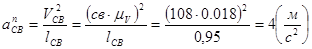
Силовой анализ механизма
Силовое исследование механизма проводим в порядке обратном структурному. Исследование будем проводить без учёта сил трения в кинематических парах. Силы тяжести прикладываем к центру масс.
К диаде (2,3) и (4,5) приложим все силы и момент сил, действующие на неё. Сила сопротивления задана графиком и имеет направление, противоположное рабочему ходу исполнительного органа Величину сил инерции определим по формулам:
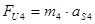 (2.9)
(2.9)
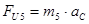 (2.10)
(2.10)
где: m4 и m5 – массы звеньев 4и5 (кг)
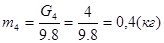
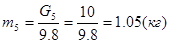
аS4 и (aС=aS5)– ускорение центров масс звеньев (м/с2).
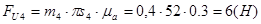
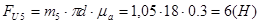
Кроме того на звено 4 действует момент пары сил инерции который имеет направление, противоположно угловому ускорению звена. Его величину определим по формуле:
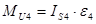 (2.11)
(2.11)
где: IS4 – осевой момент инерции звена, кг×м2; e4 – угловое ускорение звена, рад/с2.
 (2,12)
(2,12)
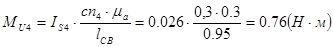
Для определения силы Ft43 составим условие моментного равновесия звена 4.
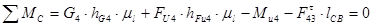 (2.13)
(2.13)
Из уравнения (2.13) будем иметь:
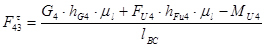 (2.14)
(2.14)
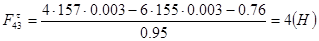
Для определения F50 и Fn43 составим векторное уравнение и строим план сил. Уравнение записываем таким образом чтобы неизвестные реакции стояли по краям уравнения. Для удобства сначала записываем силы, действующие на одно звено, а затем все силы, действующие на другое.
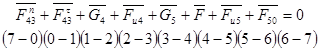 (2.15)
(2.15)
Введём масштабный коэффициент плана сил:
 (2.16)
(2.16)
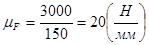
F50=520(H);
Fn43=F43=3000(H);
Рассмотрим диаду 2-3.
Определим силы инерции, действующие на звенья.
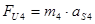 (2.17)
(2.17)
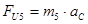 (2.18)
(2.18)
где: m2 и m3 – массы звеньев 2и3 (кг)
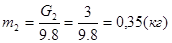
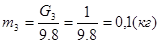
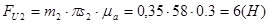
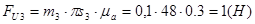
Определим момент пары сил инерции.
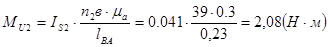
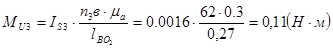
Для определения силы Ft21 составим условие моментного равновесия звена 2.
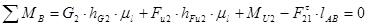 (2.19)
(2.19)
Из уравнения (2.17) будем иметь:
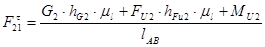 (2.20)
(2.20)
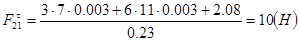
Для определения силы Ft30 составим условие моментного равновесия звена 3.
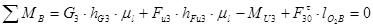 (2.21)
(2.21)
Из уравнения (2.19) будем иметь:
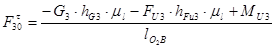 (2.22)
(2.22)
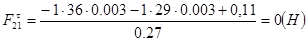
Для определения Fn30 и Fn21 составим векторное уравнение и строим план сил. Уравнение записываем таким образом чтобы неизвестные реакции стояли по краям уравнения.
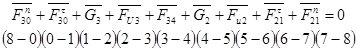 (2.23)
(2.23)
Введём масштабный коэффициент плана сил:
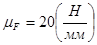
Fn30= F30=4400(H); Fn21=F21=3200(Н).
Дата: 2019-05-29, просмотров: 280.