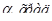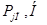В коренной шейке определяются только касательные напряжения от действия крутящего момента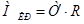 
.
Касательные напряжения от скручивающего момента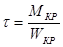 
, где
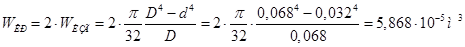
Величина крутящего момента и касательных напряжений приведены в таблице 6.
Таблица 6 – Величина крутящего момента и касательных напряжений
|
| 
| 
|
|
|
|
|
|
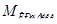
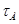
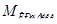
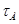
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| -66,5 | -1,1 | -23,6 | -0,4 | 332,7 | 5,7 | -23,0 | -0,4 |
| -112,1 | -1,9 | -47,6 | -0,8 | 474,8 | 8,1 | -46,1 | -0,8 |
| -123,5 | -2,1 | -71,2 | -1,2 | 464,7 | 7,9 | -68,1 | -1,2 |
| -99,9 | -1,7 | -91,3 | -1,6 | 409,1 | 7,0 | -85,4 | -1,5 |
| -51,5 | -0,9 | -102,9 | -1,8 | 361,0 | 6,2 | -92,3 | -1,6 |
| 4,7 | 0,1 | -100,5 | -1,7 | 328,7 | 5,6 | -82,7 | -1,4 |
| 52,8 | 0,9 | -81,5 | -1,4 | 302,3 | 5,2 | -52,8 | -0,9 |
| 82,7 | 1,4 | -48,8 | -0,8 | 271,9 | 4,6 | -4,7 | -0,1 |
| 92,3 | 1,6 | -13,2 | -0,2 | 233,3 | 4,0 | 51,5 | 0,9 |
| 85,4 | 1,5 | 10,1 | 0,2 | 187,8 | 3,2 | 99,9 | 1,7 |
| 68,1 | 1,2 | 9,7 | 0,2 | 139,0 | 2,4 | 123,5 | 2,1 |
| 46,1 | 0,8 | -9,8 | -0,2 | 90,7 | 1,5 | 112,1 | 1,9 |
| 23,0 | 0,4 | -20,4 | -0,3 | 44,5 | 0,8 | 66,5 | 1,1 |
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
Зная предел усталости материала вала, определим запас прочности по касательным напряжениям:;
,
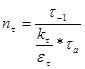где:
,
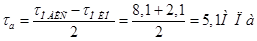Таким образом, запас прочности по касательным напряжениям для коренной шейки обеспечивается.
Расчет поршневого пальца
Расчет производится на прочность от изгибающих моментов; на предельно допустимую деформацию (овализацию) во избежание заклинивания в верхней головке шатуна; на удельное давление на его трущихся поверхностях.
Рисунок 8 – Модель поршневого пальца
При плавающем пальце для каждой точки его расчетного сечения возможен такой случай, когда в момент действия максимального усилия (таковым обычно является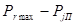 
) она окажется либо в зоне максимально растянутых, либо в зоне максимально сжатых волокон. Таким образом, в каждой точке расчетного сечения напряжение может колебаться в соответствии с изменением нагрузки от 
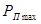до 
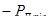, где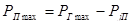 
.
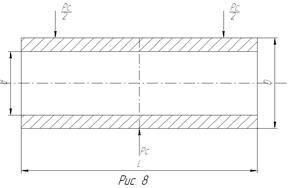
Рисунок 9 – Схема нагружения поршневого пальца
Этот случай симметричного цикла нагружения опасен с точки зрения прочности поршневого пальца и поэтому является расчетным.
Изгибающий момент
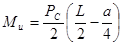
(где L – расстояние между серединами опорных участков в бобышках поршня, м; а – длина верхней головки шатуна, м; Рс – сила, действующая на палец со стороны поршня, Н, изменяем в пределах от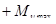 
до 
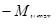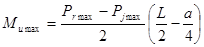, где
, где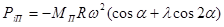 
Масса поршня
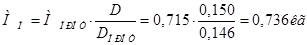
Значение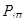 
в зависимости от угла поворота коленчатого вала приведены в таблица 7.
Таблица 7 – Значение 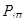в зависимости от угла поворота коленчатого вала
|
|
| 
| 
| 
|
|
| 
|
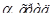
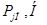
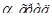
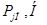
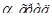
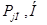
| 0,00 | -11831,50 | 51,43 | -5235,48 | 102,86 | 4348,29 | 154,29 | 6791,70 |
| 12,86 | -11347,48 | 64,29 | -2456,71 | 115,71 | 5609,74 | 167,14 | 6775,33 |
| 25,71 | -9958,18 | 77,14 | 209,64 | 128,57 | 6356,74 | 180,00 | 6756,88 |
| 38,57 | -7835,03 | 90,00 | 2529,91 | 141,43 | 6700,84 |
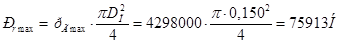
Тогда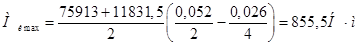 
Среднее напряжение рассматриваемого цикла равно нулю, а амплитуда цикла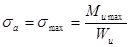 
. Момент сопротивления пальца изгибу
.
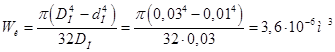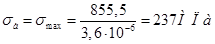
Запас прочности пальца на изгиб определяется по выражению
,
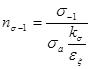где коэффициент фактора размерности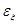 
для диаметра пальца 25мм составляет 0,92.
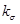- коэффициент, учитывающий влияние концентрации напряжений (связанных с резким изменением поперечного сечения) при переменных нормальных напряжениях. Так как палец не имеет скачков поперечного сечения по всей своей длине, то принимаем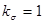 
Величина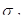 
составляет 450 МПа. Тогда
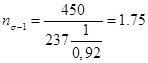
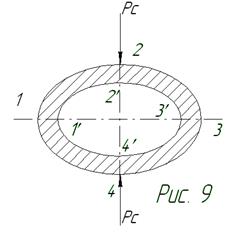
Рисунок 10 – Схема овализации поршневого пальца
Так как по этой формуле запас прочности поршневого пальца значительно занижен по сравнению с действительным запасом, то полученный запас прочности является достаточно надежным критерием оценки прочности.
Под действием силы РС палец овализируется (рисунок 10). В направлении действия РС диаметр пальца уменьшается, в противоположном направлении – увеличивается. Как показали исследования Р.С. Кинасошвили, наибольшие напряжения при овализации возникают в точках 
и 
и их величина
,
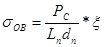где ξ=f(α), а α, в свою очередь равна
.
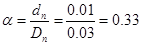Графическая зависимость ξ=f(α) приведена в пособии [4]. По ней определяем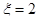 
.
Тогда
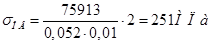
Так как допустимое напряжение овализации лежит в пределах 230-270МПа [4], то запас прочности по овализации обеспечивается.
Степень овализацци задается обычно как увеличение внешнего диаметра в направлении, перпендикулярном приложению нагрузки. Это увеличение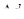 
определим по формуле Кинасошвили [4]:
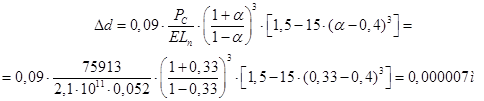
Полученная степень овализации не превышает допустимую (0,05мм), следовательно, условие незаклинивания в верхней головке шатуна соблюдается.
Удельное давление пальца на бобышки поршня:
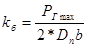, где b – длина контактирующей с пальцем поверхности бобышки
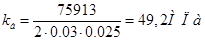
Тогда как допустимое удельное давление пальца на бобышки поршня составляет 50 МПа [4].
Расчет поршневых колец
При работе поршневое кольцо должно находиться в сжатом состоянии и создавать некоторое давление на стенки цилиндра. Величина этого давления зависит как от упругой деформации кольца, сжатого в цилиндре, так и от размеров сечения кольца.
Если принять, что средний радиус кольца в свободном состоянии равен радиусу наружной поверхности поршня (рисунок 10), то формула
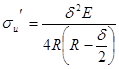
с учетом того, что 
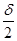обычно в 20-25 раз меньше R принимает вид
.
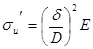Для чугунных колец Е=82500МПа. Тогда
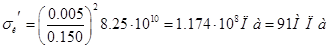
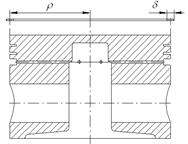
Рисунок 10 – Схема расположения и геометрические размеры кольца
Допускаемые напряжения сжатия составляют 135-150МПа, поэтому запас прочности по напряжениям сжатия удовлетворяет требованиям прочности.
Расчет поршневого кольца сделан в предположении равномерного давления кольца на стенку цилиндра. Однако теоретическое и экспериментальное изучение условий работы кольца показало целесообразность изготовления кольца с неравномерной эпюрой давления по окружности. В частности, целесообразно увеличивать давление у замка.
Величина зазора в свободном состоянии
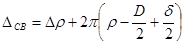. В частном случае при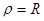 
Расчет прицепного шатуна
Производим расчет на устойчивость прицепного шатуна.
Определим осевой момент инерции сечения прицепного шатуна.
,
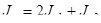где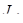 
- момент инерции прямоугольника, наиболее удаленного от оси х-х (рисунок 11)
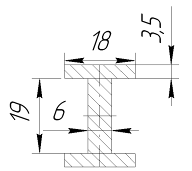
Рисунок 11 – Расчетная схема прицепного шатуна
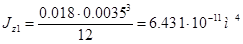
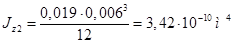
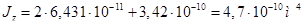
Полная площадь поперечного сечения (площадь брутто) составляет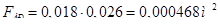 
Минимальный радиус инерции
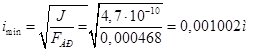
Гибкость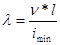 
, где n - коэффициент приведения длины, зависящий от способа заделки стержня. Рассматриваем прицепной шатун как стержень с шарнирно закрепленными концами, при этом способе n=0,7.
Тогда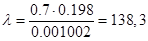 
.
Так как явление продольного изгиба существует не только в пределах упругости, но и за ними, то для определения критического напряжения нельзя пользоваться формулой Эйлера, так как она дает завышенные значения.
Теоретическое решение задачи об устойчивости за пределом пропорциональности сложно, поэтому обычно пользуются эмпирическими формулами, полученными в результате обработки большого количества опытных данных.
Определим критическое напряжение стержня по формуле Ф.С. Ясинского: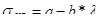 
, значения эмпирических коэффициентов a и b определяем по таблицам [5]: 
, 
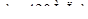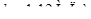. Тогда
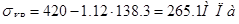
Действующее максимальное напряжение в сечении шатуна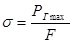 
,
.
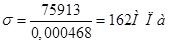Коэффициент запаса устойчивости:
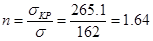
Расчет поршня
Статический расчет твердотельной модели поршня, выполненный в пакете Solid Works, производим в пакете Cosmos Works.
В основу расчета заложен метод конечных элементов (МКЭ). Перед расчетом задаем материал поршня (алюминиевый сплав), условия закрепления по плоскостям и цилиндрическим поверхностям и производим разбиение твердотельной модели на сетку конечных элементов (рисунок 13). Далее производим расчет на статическую прочность.
Рисунок 13 – Результат расчета на статическую прочность
По результатам расчета видно, что максимальные напряжения, а следовательно и минимальные коэффициенты запаса, расположились у основания бобышек (с внутренней стороны поршня) и составляют 136,7МПа, а так же на проточках под поршневые кольца (95МПа) и на периферии маслоотводных отверстий (100МПа).
Максимальные деформации характерны для диаметрально-противоположных точек “дна” поршня, расположенных в плоскости, перпендикулярной к оси поршневого пальца и составляют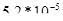 
м.
Список использованной литературы
1 . И.П. Пелепейченко, Н.И. Кормилов “Тепловые двигатели”, - Харьков: ХАИ, 1977. – 108с.
2. И.П. Пелепейченко, В.И. Крирченко “Динамический расчет авиационного однорядного звездообразного двигателя на ЭВМ”, - Харьков: ХАИ, 1982. – 56с.
3. В.И. Крирченко “ Динамический расчет поршневого звездообразного двигателя”, - Харьков: ХАИ, 1973. – 68с.
4. Ю.А. Гусев, С.В. Епифанов, А.В. Белогуб “Поршни двигателей внутреннего сгорания”, - Харьков: ХАИ, 1999. – 32с.
5. Г.С. Писаренко, В.Г. Попков “Сопротивление материалов”, - Киев: Вища школа, 1986. – 776с.
Дата: 2019-05-29, просмотров: 205.
