Схема кривошипно-шатунного механизма с прицепными шатунами показана на рисунке 2.

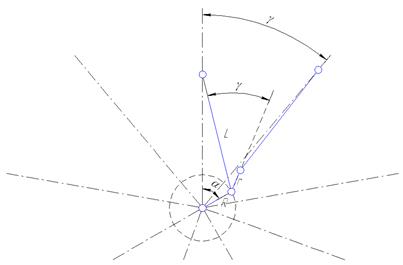
Рисунок 2 Схема кривошипно-шатунного механизма с прицепными шатунами.

Ход поршня 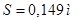 и радиус кривошипа  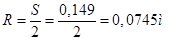найдены в тепловом расчете.

Основные размеры центрального КШМ вполне определяются радиусом 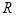 и длиной шатуна 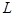. Отношение  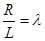принимаем таким же как и у прототипа, 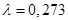. Тогда длина шатуна:

.

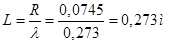Угол прицепа:

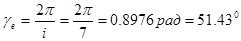
Радиусы прицепов 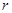 прицепных шатунов в различных цилиндрах неодинаковы. Из условия геометрического подобия следует, что

.

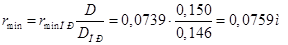В звездообразных двигателях при одинаковой длине прицепных шатунов всегда минимальным получается радиус прицепа шатунов, которые работают в цилиндрах, противоположных главному. Для семицилиндровых двигателей – это 4-й и 5-й цилиндры. Длину прицепного шатуна определяем по формуле:

,

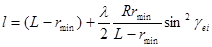где 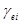 - угол между плоскостью симметрии главного шатуна и r_min.

.

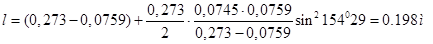Радиус остальных прицепов находим по формуле:

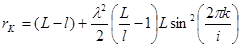, где .

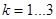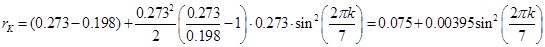
Результаты расчета сводим в таблицу 1

Таблица 1 Радиусы прицепов шатунов

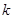
	1	2	3
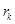
	0,078	0,79	0,076

Разнос масс КШМ с прицепными шатунами

1. Каждый прицепной шатун заменяют двумя массами, одна из которых 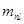 сосредотачивается на оси поршневого пальца, а другая  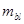– на оси прицепного шатуна.

2. Под “приведенным” главным шатуном (рисунок 3) понимают собственно главный шатун плюс массы пальцев прицепных шатунов 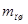 и массы 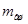, сосредоточенные на осях этих пальцев. Обозначим 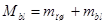; 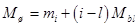. Приведенный главный шатун заменяем массами М_ПШ, сосредоточенной на оси поршневого пальца, и 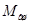, сосредоточенной на оси шатунной шейки. Величины  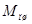и 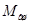 определяем из формул:

,

.

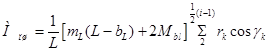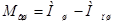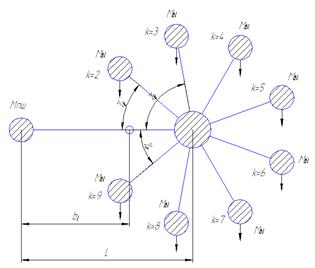
Рисунок 3 – Схема приведения масс главного шатуна.

3. Приведенная масса поступательно-движущихся частей.

Эта масса различна в цилиндрах с главным шатуном и с прицепным.

В цилиндре с прицепным шатуном

,

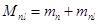где 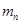 – масса комплекта поршня;

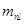 – часть массы прицепного шатуна, отнесенная к оси поршневого пальца.

В цилиндре с главным шатуном

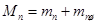
4. Приведенная масса вращательно-движущихся частей

,

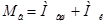где 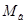- масса вращательно-движущихся частей;

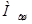 - часть массы шатуна;

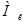– приведенная масса кривошипа.

Силы инерции

Силы инерции поступательно-движущихся масс переменны по величине и направлению и действуют по осям цилиндров. Силу инерции в цилиндре с главным шатуном находят из уравнения:

,

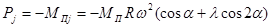а силу инерции в цилиндре с прицепным шатуном – из уравнения:

,

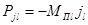где 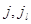 - ускорения масс  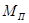и .

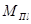Силы инерции вращательно-движущихся масс находят по формулам:

,

.

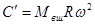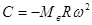Силы 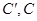, постоянные по модулю, приложены к оси шатунной шейки и направлены по радиусу кривошипа.