ВВЕДЕНИЕ
За последние годы в микроэлектронике бурное развитие получило направление, связанное с выпуском микроконтроллеров, которые предназначены для автоматизации оборудования различного назначения. Микроконтроллеры представляют собой приборы, конструктивно выполненные в виде микросхемы и включающие в себя все составные части микро-ЭВМ: микропроцессор, память данных, а также программируемые интерфейсные схемы для связи с внешней средой. Использование микроконтроллеров в системах управления обеспечивает достижение исключительно высоких показателей эффективности при столь низкой стоимости (во многих случаях система может состоять только из одного микроконтроллера), что, микроконтроллерам, видимо, нет разумной альтернативной элементной базы для построения управляющей и/или регулирующих систем. Более двух третей мирового рынка микропроцессорных средств составляют именно микроконтроллеры.
Перед автоматизацией производства ставят следующие задачи:
- переход от автоматизации отдельных простейших производственных операций к комплексной автоматизации средств производства и производственных процессов;
- повысить точность автоматических систем (разработка самонастраивающихся и многомерных систем автоматического управления);
- переход к использованию цифровых средств автоматизации (использование ЭВМ).
Привод подач является одним из основных узлов, определяющих производительность и точность станков с ЧПУ. Система ЧПУ позволяет практически безинерционно сформировать сигналы управления приводом, обеспечивающие позиционирование в заданной координате. В этих условиях важное значение имеет совершенствование параметров исполнительного механизма, схемы его управления с учётом особенностей кинематической цепи привода.
В приводах подач станков с ЧПУ часто применяются двигатели постоянного тока с возбуждением от постоянных магнитов, преимуществом которых является высокая линейность механических характеристик. Это позволяет плавно регулировать частоту вращения вала в широких пределах (1000 и выше), а также способность длительной работы на малых оборотах с высоким крутящим моментом. При этом значительно упрощается кинематика станка, увеличивается надёжность и точность работы. Двигатели постоянного тока совершенствуются в направлении повышения быстродействия и увеличения перегрузочной способности, повышения КПД, равномерности вращения на низких скоростях и т. д. Для питания двигателей постоянного тока используют тиристорные и широтно-импульсные преобразователи, обладающие высокими технико-экономическими показателями.
Устройство ЧПУ, которое управляет приводом, реализуется на микропроцессорных комплектах или специализированном контроллере. Системы ЧПУ обеспечивают автоматическое программное управление скоростью и положением рабочих органов в режиме реального времени.
1. АНАЛИЗ ОСНОВНЫХ ТРЕБОВАНИЙ И ПОСТАНОВКА ЗАДАЧ ПРОЕКТИРОВАНИЯ
1.1 Расчеты основных параметров электромеханической системы привода
В данном курсовом проекте разрабатывается привод подач токарного станка. Для перемещения по координате предусмотрен свой привод. Поэтому разработку производим для одного контура управления. Применение ЦСУ позволяет значительно повысить точность и качество обработки, упростить кинематику привода подач, избежать применения многоступенчатого редуктора, повысить технологические возможности станка. Кинематическая схема привода подач изображена на рисунке 1.1. Вращательное движение от электродвигателя через одноступенчатый редуктор Р передается на ходовой винт. Через передачу винт-гайка вращательное движение преобразуется в поступательное движение суппорта С. На ходовом винте установлен кодовый датчик (КОД) положения, позволяющий контролировать также частоту вращения винта путем цифрового дифференцирования.
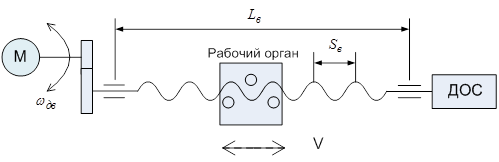
Рисунок 1.1 - Кинематическая схема привода
Такая система обеспечивает глубокое регулирование скорости и высокоточный контроль перемещения стола по координате.
Станок токарный предназначен выполнять токарную обработку деталей и нарезку резьбы на телах вращения (валы, диски и т.д.) из стали.
По согласованию с изготовителем станок оснащается суппортом с одним плоским резцедержателем, накладным отрезным резцедержателем или четырёх позиционной головкой с вертикальной осью вращения.
Область применения станка – различные отрасли промышленности.
Связав технические характеристики с параметрами, указанными в задании, произведём расчет и выбор электродвигателя привода подачи суппорта станка.
Мощность, затрачиваемая на рабочей подаче с учетом всех сил:
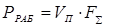 , (1.1)
, (1.1)
где VП=17 м/мин – максимальная скорость подачи;
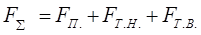 , (1.2)
, (1.2)
где FП =7 кН – сила подачи, FТ.Н.  – сила трения в направляющих;
– сила трения в направляющих;
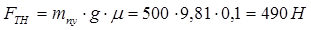 (1.3)
(1.3)
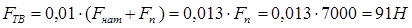 (1.4)
(1.4)
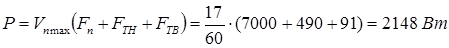 (1.5)
(1.5)
Тогда требуемая мощность определится:
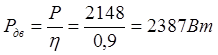 , (1.6)
, (1.6)
где h-К.П.Д. двигателя, h=0.9;
Исходя из расчётов необходимой мощности, предварительно выбираем электродвигатель типа ПБВ-132L. Характеристики ЭД типа ПБВ-132L представлены в таблице 1.1.
Таблица 1.1 - Характеристики ЭД типа ПБВ-112
| Номинальный момент, Н×м | 47,7 |
| Номинальная скорость, об/мин | 600 |
| Номинальная мощность, кВт | 3,0 |
| Номинальное напряжение, В | 70 |
| Номинальный ток, А | 50 |
| Максимальный момент, Н×м | 470 |
| Максимальная скорость, об/мин | 2000 |
| Момент инерции якоря, кг-м2* | 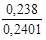
|
| Максимальное ускорение, с-2 | 1970 |
| Электромеханическая постоянная, мс | 12,3 |
| Электромагнитная пост., мс | 7,85 |
Из ряда типовых размеров винтов выбираем винт со следующими параметрами (см. Таблица 1.2)
Таблица 1.2 – Размер винта
| Диаметр винта Dв, мм | Диаметр шарика d, мм | Шаг винта | Общее количество витков в двух гайках | Грузоподъемность, кН | Осевая податливость еx -9,м/Н | |
| статическая Qст | динамическая Qд | |||||
| 80 | 6 | 10 | 6 | 100 | 25 | 0,528 |
Осуществляем проверку правильности выбора ЭД путем расчетов работы в статическом и динамическом режимах.
В статическом режиме работы статический момент сопротивления [2]:
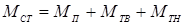 , (1.7)
, (1.7)
где МП – момент сопротивления от усилия подачи на рабочем ходу, Н×м;
МТВ – момент трения в кинематических парах (подшипниках) ходового винта, Н×м;
МТН – момент сил трения в направляющих, Н×м.
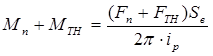 (1.8)
(1.8)
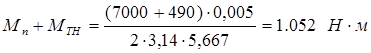 ,
,
где 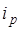 – передаточное отношение редуктора, определяемое из соотношения
– передаточное отношение редуктора, определяемое из соотношения
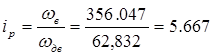 , (1.9)
, (1.9)
где wВМАХ – максимальная скорость вращения винта, с-1;
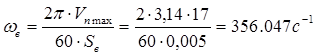 . (1.10)
. (1.10)
Таким образом:
Определим момент трения винта:
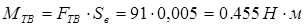 ; (1.11)
; (1.11)
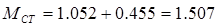 (Н∙м).
(Н∙м).
Двигатель обеспечивает длительную работу под нагрузкой, т.к. МСТ<МДВ
(1.507 Н×м < 47.7 Н×м).
Проверить двигатель в динамическом режиме.
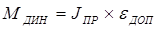 , (1.12)
, (1.12)
где JПР – приведенный момент инерции механизма привода подач станка, кг×м2;
eДОП – максимально допустимое угловое ускорение двигателя на рабочем ходу, с-2.
Определим eДОП из условия: 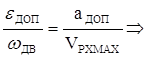 (1.13)
(1.13)
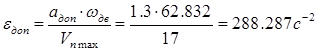 (1.14)
(1.14)
где аДОП – допустимое ускорение при разгоне, аДОП=1.3 м/с2.
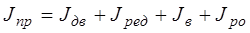 , (1.15)
, (1.15)
где 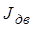 – техническая характеристика двигателя;
– техническая характеристика двигателя;
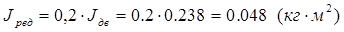
JДВ – момент инерции двигателя, JДВ=0,238 кг×м2.
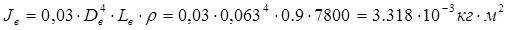 , (1.16)
, (1.16)
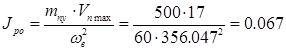 (кг×м2); (1.17)
(кг×м2); (1.17)
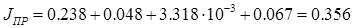 (кг×м2). (1.18)
(кг×м2). (1.18)
Таким образом, динамический момент сопротивления:
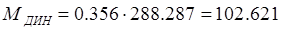 (Н∙м) (1.19)
(Н∙м) (1.19)
Максимальный динамический момент, который может обеспечить двигатель, равен:
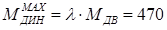 (Н×м). (1.20)
(Н×м). (1.20)
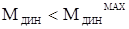 (102.621 < 470).
(102.621 < 470).
В статическом и динамическом режиме двигатель обеспечивает необходимый момент для преодоления сил сопротивления, следовательно, выбор сделан правильно.
ВВЕДЕНИЕ
За последние годы в микроэлектронике бурное развитие получило направление, связанное с выпуском микроконтроллеров, которые предназначены для автоматизации оборудования различного назначения. Микроконтроллеры представляют собой приборы, конструктивно выполненные в виде микросхемы и включающие в себя все составные части микро-ЭВМ: микропроцессор, память данных, а также программируемые интерфейсные схемы для связи с внешней средой. Использование микроконтроллеров в системах управления обеспечивает достижение исключительно высоких показателей эффективности при столь низкой стоимости (во многих случаях система может состоять только из одного микроконтроллера), что, микроконтроллерам, видимо, нет разумной альтернативной элементной базы для построения управляющей и/или регулирующих систем. Более двух третей мирового рынка микропроцессорных средств составляют именно микроконтроллеры.
Перед автоматизацией производства ставят следующие задачи:
- переход от автоматизации отдельных простейших производственных операций к комплексной автоматизации средств производства и производственных процессов;
- повысить точность автоматических систем (разработка самонастраивающихся и многомерных систем автоматического управления);
- переход к использованию цифровых средств автоматизации (использование ЭВМ).
Привод подач является одним из основных узлов, определяющих производительность и точность станков с ЧПУ. Система ЧПУ позволяет практически безинерционно сформировать сигналы управления приводом, обеспечивающие позиционирование в заданной координате. В этих условиях важное значение имеет совершенствование параметров исполнительного механизма, схемы его управления с учётом особенностей кинематической цепи привода.
В приводах подач станков с ЧПУ часто применяются двигатели постоянного тока с возбуждением от постоянных магнитов, преимуществом которых является высокая линейность механических характеристик. Это позволяет плавно регулировать частоту вращения вала в широких пределах (1000 и выше), а также способность длительной работы на малых оборотах с высоким крутящим моментом. При этом значительно упрощается кинематика станка, увеличивается надёжность и точность работы. Двигатели постоянного тока совершенствуются в направлении повышения быстродействия и увеличения перегрузочной способности, повышения КПД, равномерности вращения на низких скоростях и т. д. Для питания двигателей постоянного тока используют тиристорные и широтно-импульсные преобразователи, обладающие высокими технико-экономическими показателями.
Устройство ЧПУ, которое управляет приводом, реализуется на микропроцессорных комплектах или специализированном контроллере. Системы ЧПУ обеспечивают автоматическое программное управление скоростью и положением рабочих органов в режиме реального времени.
1. АНАЛИЗ ОСНОВНЫХ ТРЕБОВАНИЙ И ПОСТАНОВКА ЗАДАЧ ПРОЕКТИРОВАНИЯ
1.1 Расчеты основных параметров электромеханической системы привода
В данном курсовом проекте разрабатывается привод подач токарного станка. Для перемещения по координате предусмотрен свой привод. Поэтому разработку производим для одного контура управления. Применение ЦСУ позволяет значительно повысить точность и качество обработки, упростить кинематику привода подач, избежать применения многоступенчатого редуктора, повысить технологические возможности станка. Кинематическая схема привода подач изображена на рисунке 1.1. Вращательное движение от электродвигателя через одноступенчатый редуктор Р передается на ходовой винт. Через передачу винт-гайка вращательное движение преобразуется в поступательное движение суппорта С. На ходовом винте установлен кодовый датчик (КОД) положения, позволяющий контролировать также частоту вращения винта путем цифрового дифференцирования.

Рисунок 1.1 - Кинематическая схема привода
Такая система обеспечивает глубокое регулирование скорости и высокоточный контроль перемещения стола по координате.
Станок токарный предназначен выполнять токарную обработку деталей и нарезку резьбы на телах вращения (валы, диски и т.д.) из стали.
По согласованию с изготовителем станок оснащается суппортом с одним плоским резцедержателем, накладным отрезным резцедержателем или четырёх позиционной головкой с вертикальной осью вращения.
Область применения станка – различные отрасли промышленности.
Связав технические характеристики с параметрами, указанными в задании, произведём расчет и выбор электродвигателя привода подачи суппорта станка.
Мощность, затрачиваемая на рабочей подаче с учетом всех сил:
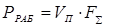 , (1.1)
, (1.1)
где VП=17 м/мин – максимальная скорость подачи;
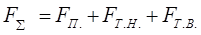 , (1.2)
, (1.2)
где FП =7 кН – сила подачи, FТ.Н.  – сила трения в направляющих;
– сила трения в направляющих;
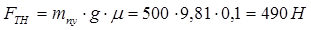 (1.3)
(1.3)
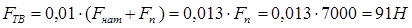 (1.4)
(1.4)
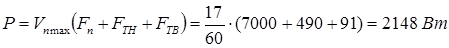 (1.5)
(1.5)
Тогда требуемая мощность определится:
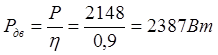 , (1.6)
, (1.6)
где h-К.П.Д. двигателя, h=0.9;
Исходя из расчётов необходимой мощности, предварительно выбираем электродвигатель типа ПБВ-132L. Характеристики ЭД типа ПБВ-132L представлены в таблице 1.1.
Таблица 1.1 - Характеристики ЭД типа ПБВ-112
| Номинальный момент, Н×м | 47,7 |
| Номинальная скорость, об/мин | 600 |
| Номинальная мощность, кВт | 3,0 |
| Номинальное напряжение, В | 70 |
| Номинальный ток, А | 50 |
| Максимальный момент, Н×м | 470 |
| Максимальная скорость, об/мин | 2000 |
| Момент инерции якоря, кг-м2* | 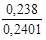
|
| Максимальное ускорение, с-2 | 1970 |
| Электромеханическая постоянная, мс | 12,3 |
| Электромагнитная пост., мс | 7,85 |
Из ряда типовых размеров винтов выбираем винт со следующими параметрами (см. Таблица 1.2)
Таблица 1.2 – Размер винта
| Диаметр винта Dв, мм | Диаметр шарика d, мм | Шаг винта | Общее количество витков в двух гайках | Грузоподъемность, кН | Осевая податливость еx -9,м/Н | |
| статическая Qст | динамическая Qд | |||||
| 80 | 6 | 10 | 6 | 100 | 25 | 0,528 |
Осуществляем проверку правильности выбора ЭД путем расчетов работы в статическом и динамическом режимах.
В статическом режиме работы статический момент сопротивления [2]:
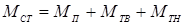 , (1.7)
, (1.7)
где МП – момент сопротивления от усилия подачи на рабочем ходу, Н×м;
МТВ – момент трения в кинематических парах (подшипниках) ходового винта, Н×м;
МТН – момент сил трения в направляющих, Н×м.
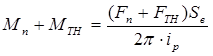 (1.8)
(1.8)
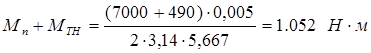 ,
,
где 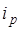 – передаточное отношение редуктора, определяемое из соотношения
– передаточное отношение редуктора, определяемое из соотношения
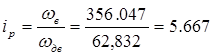 , (1.9)
, (1.9)
где wВМАХ – максимальная скорость вращения винта, с-1;
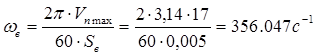 . (1.10)
. (1.10)
Таким образом:
Определим момент трения винта:
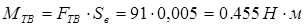 ; (1.11)
; (1.11)
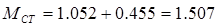 (Н∙м).
(Н∙м).
Двигатель обеспечивает длительную работу под нагрузкой, т.к. МСТ<МДВ
(1.507 Н×м < 47.7 Н×м).
Проверить двигатель в динамическом режиме.
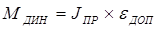 , (1.12)
, (1.12)
где JПР – приведенный момент инерции механизма привода подач станка, кг×м2;
eДОП – максимально допустимое угловое ускорение двигателя на рабочем ходу, с-2.
Определим eДОП из условия: 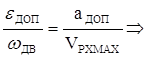 (1.13)
(1.13)
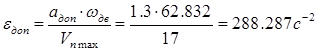 (1.14)
(1.14)
где аДОП – допустимое ускорение при разгоне, аДОП=1.3 м/с2.
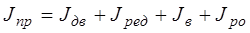 , (1.15)
, (1.15)
где  – техническая характеристика двигателя;
– техническая характеристика двигателя;
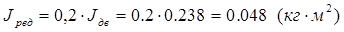
JДВ – момент инерции двигателя, JДВ=0,238 кг×м2.
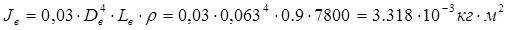 , (1.16)
, (1.16)
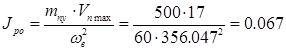 (кг×м2); (1.17)
(кг×м2); (1.17)
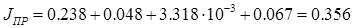 (кг×м2). (1.18)
(кг×м2). (1.18)
Таким образом, динамический момент сопротивления:
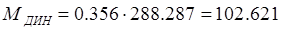 (Н∙м) (1.19)
(Н∙м) (1.19)
Максимальный динамический момент, который может обеспечить двигатель, равен:
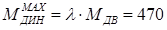 (Н×м). (1.20)
(Н×м). (1.20)
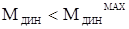 (102.621 < 470).
(102.621 < 470).
В статическом и динамическом режиме двигатель обеспечивает необходимый момент для преодоления сил сопротивления, следовательно, выбор сделан правильно.
Расчет основных параметров системы управления
Одной из основных характеристик системы управления является период дискретности 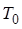 . Для систем с астатизмом первого порядка период дискретности определяется допустимой величиной скоростной ошибки
. Для систем с астатизмом первого порядка период дискретности определяется допустимой величиной скоростной ошибки 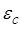 и допускаемым ускорением
и допускаемым ускорением 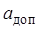 :
:
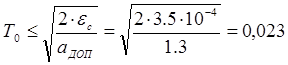 (с). (1.21)
(с). (1.21)
Однако расчет 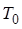 по этой формуле гарантирует соблюдение лишь одного условия – траектория ускоренного движения рабочего органа за время
по этой формуле гарантирует соблюдение лишь одного условия – траектория ускоренного движения рабочего органа за время 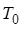 не отклонится от заданной траектории больше, чем на величину
не отклонится от заданной траектории больше, чем на величину 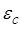 .
.
Следует учесть, что при проектировании привода необходимо обеспечить устойчивость и требуемую полосу частотного диапазона. Эти параметры зависят от периода дискретности 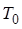 , величина которого определяет форму частотной характеристики в высокочастотном диапазоне. Поэтому необходимо сначала построить желаемую частотную характеристику системы, а затем определить период дискретности.
, величина которого определяет форму частотной характеристики в высокочастотном диапазоне. Поэтому необходимо сначала построить желаемую частотную характеристику системы, а затем определить период дискретности.
На рисунке 1.2 изображена желаемая логарифмическая амплитудно-частотная характеристика (ЛАЧХ), форма которой позволяет:
· устранить позиционную ошибку – первая асимптота имеет наклон к оси частот 20 дБ/дек;
· ограничить скоростную ошибку – первая асимптота должна занять определенное положение на оси относительной амплитуды 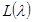 ;
;
· обеспечить устойчивую работу привода – ЛАЧХ имеет асимптоту, которая пересекает ось частот с наклоном 20 дБ/дек;
· обеспечить требуемый частотный диапазон привода и показатель колебательности – должна быть обеспечена необходимая длина асимтоты в частотном диапазоне 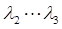 .
.
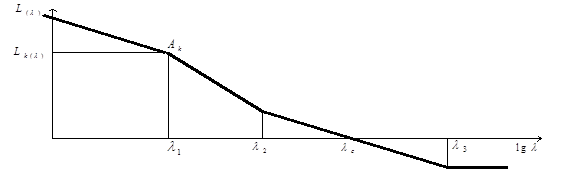
Рисунок 1.2 – желаемая форма ЛАЧХ цифрового электропривода
Желаемая ЛАЧХ описывается следующей дискретной частотной характеристики (ДЧХ):
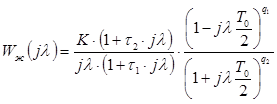 , (1.22)
, (1.22)
где 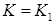 ;
; 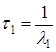 ;
; 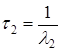 ;
; 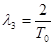 – основные параметры, определяемые требованиями к системе электропривода;
– основные параметры, определяемые требованиями к системе электропривода;
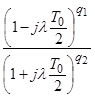 – характеристика запаздывания, определяемая параметрами цифровой системы.
– характеристика запаздывания, определяемая параметрами цифровой системы.
Для определения основных параметров ДЧХ необходимо преобразовать заданные параметры технологического процесса в эквивалентные параметры гармонического сигнала, которые позволяют определить положение критической точки 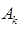 запретной области ЛАЧХ.
запретной области ЛАЧХ.
Преобразования параметров возможны в тех случаях, когда движения рабочих органов задаются в виде круговых траекторий. При развертке во времени одной из координат круговой траектории движения получим синусоиду:
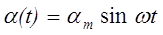 , (1.23)
, (1.23)
поверхности; 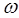 – угловая скорость (подача).
– угловая скорость (подача).
Первая и вторая производные (скорость и ускорение) гармонического сигнала определяются известными выражениями:
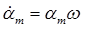 (1.24)
(1.24)
где индексы 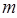 обозначают максимальные (допускаемые) значения.
обозначают максимальные (допускаемые) значения.
Отсюда можно определить эквивалентные параметры гармонического воздействия – частоту и амплитуду:
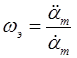 ,
, 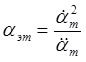 . (1.25)
. (1.25)
Максимальная ошибка для дискретной системы определяется выражением:
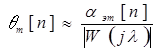 , (1.26)
, (1.26)
где 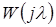 – дискретная частотная характеристика системы,
– дискретная частотная характеристика системы, 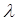 – псевдочастота.
– псевдочастота.
Для низкочастотного участка ЛАЧХ справедливо допущение 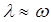 . Тогда:
. Тогда:
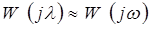 . (1.27)
. (1.27)
Если известно значение ошибки 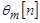 , то должно быть выполнено условие:
, то должно быть выполнено условие:
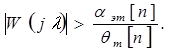
 (1.28)
(1.28)
Для относительной амплитуды 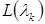 это условие запишется в следующем виде:
это условие запишется в следующем виде:
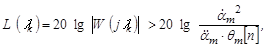 (1.29)
(1.29)
В системах управления электроприводами значения максимальной скорости 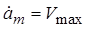 , допускаемого ускорения
, допускаемого ускорения 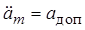 и допускаемой скоростной ошибки
и допускаемой скоростной ошибки 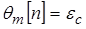 известны.
известны.
Тогда, учитывая условия преобразования, для обеспечения необходимой точности желаемая ЛАЧХ должна проходить выше критической точки 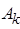 с координатами:
с координатами:
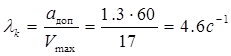 ; (1.30)
; (1.30)
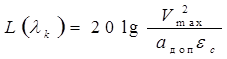 . (1.31)
. (1.31)
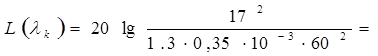 44.932 дБ
44.932 дБ
При этом запретная область ограничивается по относительной амплитуде первой асимптотой, которая проводится влево от точки 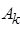 с наклоном -20 дБ/дек. По частоте эта запретная область ограничивается второй асимптотой, которая проводится вправо от точки
с наклоном -20 дБ/дек. По частоте эта запретная область ограничивается второй асимптотой, которая проводится вправо от точки 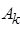 с наклоном -40 дБ/дек. Положение запретной зоны показано на рисунке 1.3.
с наклоном -40 дБ/дек. Положение запретной зоны показано на рисунке 1.3.
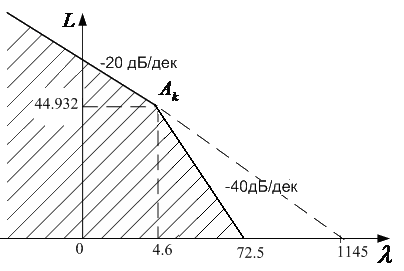
Рисунок 1.3 – Построение запретной зоны по критериям точности
Скоростная ошибка 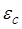 определяет необходимую добротность системы по скорости
определяет необходимую добротность системы по скорости 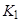 , которая определяется по формуле:
, которая определяется по формуле:
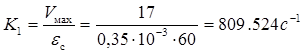 , (1.32)
, (1.32)
Значение 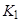 соответствует точке пересечения линии, которая продолжает первую низкочастотную асимптоту, с осью
соответствует точке пересечения линии, которая продолжает первую низкочастотную асимптоту, с осью 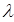 .
.
После построения запретной области строятся логарифмические амплитудные и фазовые частотные характеристики. При построении следует придерживаться следующего порядка.
1. Первая низкочастотная асимптота желаемой ЛАХ проводится с наклоном –20 дБ/дек выше точки 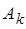 на 3 дБ, чтобы обеспечить запас устойчивости. Подъем характеристики приводит к увеличению коэффициента добротности по скорости в
на 3 дБ, чтобы обеспечить запас устойчивости. Подъем характеристики приводит к увеличению коэффициента добротности по скорости в 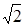 раза:
раза:
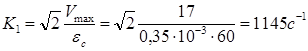 . (1.33)
. (1.33)
2. Вторая асимптота проводится с наклоном –40 дБ/дек от точки сопряжения с координатами ( 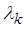 ;
; 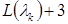 ) до точки пересечения с осью , которая определяет базовую частоту
) до точки пересечения с осью , которая определяет базовую частоту 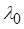 запретной области:
запретной области:
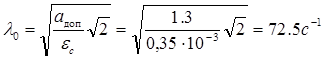 . (1.34)
. (1.34)
3. По заданному показателю колебательности 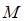 определяется частота сопряжения второй и третьей асимптот:
определяется частота сопряжения второй и третьей асимптот:
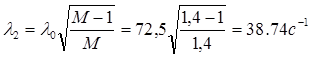 . (1.35)
. (1.35)
4. Третья асимптота с наклоном –20 дБ/дек проводится от точки 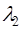 до точки
до точки 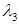 , которая определяется из условия обеспечения требуемого показателя колебательности:
, которая определяется из условия обеспечения требуемого показателя колебательности:
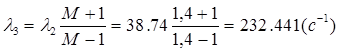 . (1.36)
. (1.36)
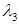 вычисляется по соотношению:
вычисляется по соотношению:
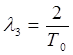 . (1.37)
. (1.37)
5. Строится график 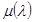 запретной области фазовой частотной характеристики:
запретной области фазовой частотной характеристики:
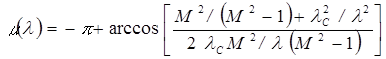 . (1.38)
. (1.38)
где 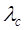 – частота среза, которая определяется по формуле:
– частота среза, которая определяется по формуле:
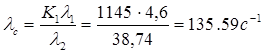 . (1.39)
. (1.39)
6. Строится график фазовой частотной характеристики 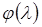 :
:
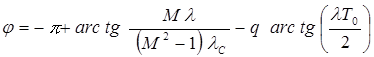 . (1.40)
. (1.40)
где 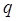 – показатель эквивалентного запаздывания, значение которого принимается равным 1.
– показатель эквивалентного запаздывания, значение которого принимается равным 1.
На рисунке 1.4 показано положение запретной области 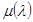 и фазовой частотной характеристики
и фазовой частотной характеристики 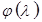 .
.
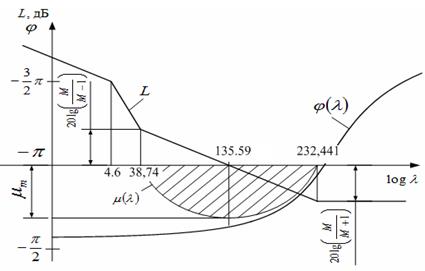
Рисунок 1.4 – Построение запретной области для фазовой характеристики
Построенные графики позволяют сделать вывод о запасе устойчивости системы управления по фазе. Фазовая характеристика не должна заходить в запретную область, для которой относительная логарифмическая амплитуда находится в пределах:
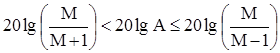 . (1.41)
. (1.41)
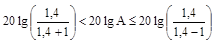 (1.42)
(1.42)
Если же это условие не выполняется, то желаемый результат можно получить путем изменения частот сопряжения 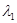 и
и 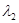 , а также коэффициента
, а также коэффициента 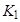 .
.
В верхнем диапазоне частота 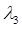 определяет период дискретности
определяет период дискретности 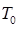 в соответствии с выражением:
в соответствии с выражением:
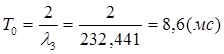 . (1.43)
. (1.43)
Это значение и должно быть принято в последующих расчетах.
2. РАЗРАБОТКА ФУНКЦИОНАЛЬНОЙ СХЕМЫ
Задачи проектирования систем управления на локальном уровне, чаще всего, касаются систем электроприводов, выполняющих определенные рабочие движения. В технологическом оборудовании машиностроительного производства используются регулируемые и следящие электроприводы с двигателями постоянного или переменного тока.
Пример функциональной схемы следящего электропривода с двигателем постоянного тока приведен на рисунке 2.1.
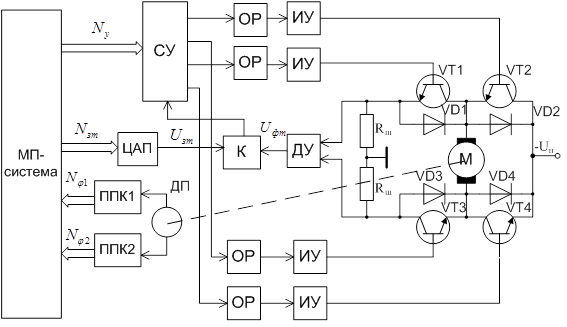
Рисунок 2.1 – Функциональная схема следящего электропривода с ШИП и релейным контуром тока
В этом следящем электроприводе измерительная система имеет двухотсчетный преобразователь перемещение-код (ППК1 и ППК2). В контуре тока в качестве датчиков обратной связи применены шунты RШ. Для усиления напряжения, которое снимается с шунтов (UШ = 0...75 мВ), и формирования двухполярного сигнала используется дифференциальный усилитель ДУ. Выходное напряжение усилителя 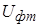 , соответствующее фактическому значению тока, через гальваническую развязку поступает на один вход компаратора К, а на другой подается выходное напряжение цифро-аналогового преобразователя (ЦАП), который преобразует код задания тока
, соответствующее фактическому значению тока, через гальваническую развязку поступает на один вход компаратора К, а на другой подается выходное напряжение цифро-аналогового преобразователя (ЦАП), который преобразует код задания тока 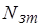 в аналоговый сигнал задания
в аналоговый сигнал задания 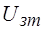 .
.
Логический сигнал с выхода компаратора поступает на схему управления СУ, которая предназначена для преобразования кода управления 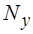 в длительности импульсов переключения силовых транзисторов. Эти импульсы через оптронную развязку ОР и импульсные усилители ИУ подаются на базы транзисторных ключей VT1…VT4, образующих мостовую схему. С целью устранения сквозных токов при переключении пар организуется безтоковая пауза. В качестве силовых элементов применены биполярные транзисторы ТКД.
в длительности импульсов переключения силовых транзисторов. Эти импульсы через оптронную развязку ОР и импульсные усилители ИУ подаются на базы транзисторных ключей VT1…VT4, образующих мостовую схему. С целью устранения сквозных токов при переключении пар организуется безтоковая пауза. В качестве силовых элементов применены биполярные транзисторы ТКД.
Информация с преобразователей перемещение-код сравнивается с кодом задания, ошибка обрабатывается с помощью программы регулятора, который выполняет расчет кода управления 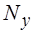 и уровня ограничения тока
и уровня ограничения тока 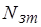 в функции скорости. Для регулирования приняты: пропорциональный закон в контуре положения с введением сигнала компенсации скоростной ошибки и пропорционально-интегрально-дифференциальный (ПИД) закон в контуре скорости. Период дискретности системы управления составляет 1 мс.
в функции скорости. Для регулирования приняты: пропорциональный закон в контуре положения с введением сигнала компенсации скоростной ошибки и пропорционально-интегрально-дифференциальный (ПИД) закон в контуре скорости. Период дискретности системы управления составляет 1 мс.
На рынке Украины широко представлены микроконтроллеры известных фирм SIEMENS, ABB, INTEL и многих других. Микропроцессоры серии ARM7 компании PHILIPS не уступают аналогам по техническими и экономическими характеристиками. Преимуществом микропроцессоров данной серии есть большое количество технической документации и легкий доступ к ней.
Структурная схема микроконтроллера LPC2148 представлена на рис. 2.2.
Для работы контроллера необходимо одно источник питания +3В. Через два программируемых порта ввода/вывода LPC2148 взаимодействует со средой в стандарте ТТЛ-схем с тремя состояниями выхода.
Важной особенностью АЛУ является его способность оперировать не только байтами, но и битами.
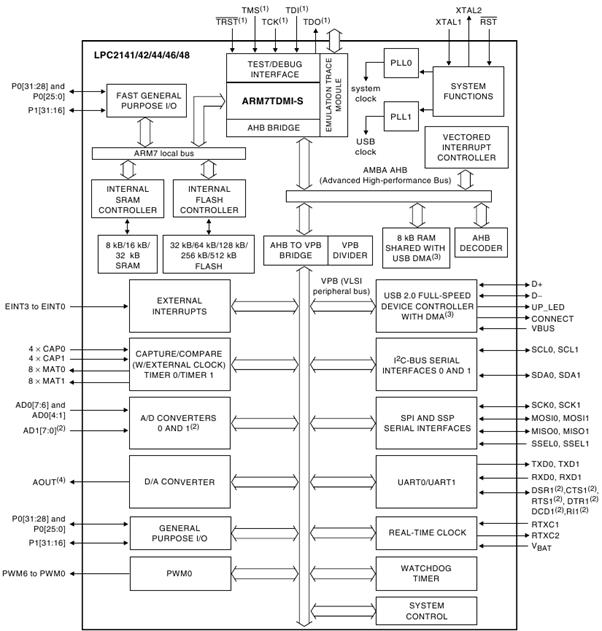
Рисунок 2.2 – Структурная схема микроконтроллера LPC2148
Контроллер LPC2148 как видно из рисунка имеет:
тестовый интерфейс, позволяющий проводить пошаговое выполнение программы;
ОЗУ память ;
FLASH память;
векторный контроллер прерываний;
интерфейсы SSP, SPI, I2C;
два UART;
часы реального времени;
ЦАП ;
два АЦП;
два таймера захвата/сравнения;
WDT;
Два режима работы обычный и экономный;
Кварцевый резонатор, который подключается к внешним выводам ХTAL1 и ХTAL2, управляет работой внутреннего генератора, который в свою очередь формирует сигналы синхронизации.
3. МЕТОДИКА МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ПРИВОДА ПОСТОЯННОГО ТОКА ДИСКРЕТНЫМИ ФУНКЦИЯМИ
Применение цифровых систем управления электроприводами постоянного тока требует особого подхода к их математическому описанию и моделированию. Это обусловлено наличием квантования непрерывных функций (тока, скорости, положения) по уровню и времени, а также запаздыванием результатов расчетов.
Для анализа и синтеза цифровых систем управления применяют метод дискретных передаточных функций (ДПФ) и метод дискретных частотных характеристик (ДЧХ).
Первый метод дает возможность оптимизировать динамические характеристики во временной области, однако на практике его применение ограничивается системами невысокого порядка.
Метод ДЧХ позволяет осуществлять синтез регулятора в частотной области. Он значительно проще метода ДПФ, однако его применение возможно только при определенных соотношениях между частотой квантования, частотой среза и малыми постоянными времени. Синтезированный по этому метода регулятор не является строго оптимальным; так как фактически метод основан на аналогии дискретных и непрерывных систем при малых значениях периода квантования. Однако если учесть, что система управления приводом строится по структуре подчиненного регулирования, метод ДЧХ является единственным средством математического описания привода.
Модель цифрового электропривода может быть представлена двумя частями – неизменяемой частью (НЧ), которая охватывает все элементы объекта (преобразователь, двигатель, кинематическую схему и др.) и дискретной частью (МП-система), которая реализует корректирующий алгоритм цифрового регулятора.
Структурная схема цифровой системы электропривода представлена на рисунке 3.1.
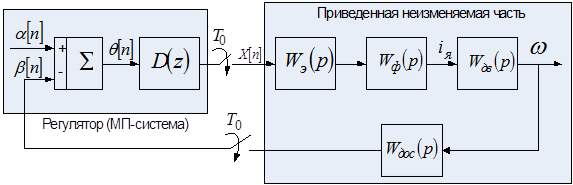
Рисунок 3.1 – Структурная схема системы электропривода
Неизменяемая часть описывается обычно дифференциальными уравнениями, представленными передаточной функцией 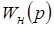 , а цифровые регуляторы – уравнениями в разностной форме, представленными передаточной функцией
, а цифровые регуляторы – уравнениями в разностной форме, представленными передаточной функцией 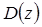 .
.
Единое представление этих частей системы может быть получено с помощью z-преобразования и связанного с ним билинейного w-преобразования.
Задающее воздействие 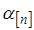 и сигнал обратной связи
и сигнал обратной связи 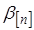 представляют собой решетчатые функции. Функция сигнала ошибки
представляют собой решетчатые функции. Функция сигнала ошибки 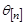 под действием корректирующего алгоритма цифрового регулятора, описываемого дискретной передаточной функцией (ДПФ)
под действием корректирующего алгоритма цифрового регулятора, описываемого дискретной передаточной функцией (ДПФ) 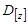 , превращается в решетчатую функцию управления
, превращается в решетчатую функцию управления 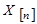 . Соединение дискретной части с неизменяемой частью обеспечиваются фиксатором.
. Соединение дискретной части с неизменяемой частью обеспечиваются фиксатором.
Выходной сигнал фиксатора, например, регистра или цифро-аналогового преобразователя, должен быть экстраполированным, то есть преобразованным в непрерывную форму. Обычно сигнал экстраполируется функцией нулевого порядка 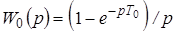 .
.
Объединив экстраполятор с неизменяемой частью, получим приведенную неизменяемую часть с передаточной функцией:
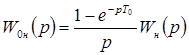 . (3.1)
. (3.1)
Дискретная передаточная функция неизменяемой части представляется Z-преобразованием:
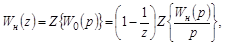 (3.2)
(3.2)
где 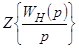 – z-преобразование передаточной функции приведенной неизменяемой части;
– z-преобразование передаточной функции приведенной неизменяемой части; 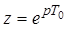 .
.
Неизменяемая часть включает в себя экстраполятор, формирователь тока якоря, двигатель постоянного тока и датчик обратной связи, которые описываются передаточными функциями – 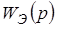 ,
, 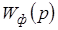 ,
, 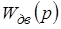
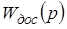 , соответственно.
, соответственно.
Передаточная функция формирователя тока описывает соединение двух звеньев, включенных последовательно и образующих единую систему – преобразователь (ТП или ШИП) и якорную цепь двигателя. В результате такого объединения исключается математическое описание преобразователя, который имеет сложную форму выходного напряжения, и математический анализ производится относительно импульсов тока якоря, форма которых проще. При этом передаточная функция формирователя тока приобретает следующий вид:
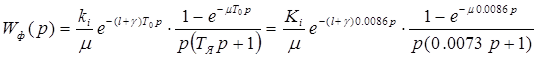 , (3.3)
, (3.3)
где 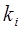 – коэффициент передачи по току;
– коэффициент передачи по току;
 – относительная длительность импульса напряжения (
– относительная длительность импульса напряжения ( 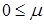 <1);
<1);
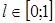 – целое число периодов дискретности
– целое число периодов дискретности 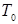 , на которое запаздывает импульс напряжения относительно времени подачи управляющего сигнала, принимаем l=1 (для ШИП);
, на которое запаздывает импульс напряжения относительно времени подачи управляющего сигнала, принимаем l=1 (для ШИП);
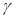 – дробная часть периода дискретности
– дробная часть периода дискретности 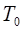 (0<
(0< 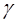 <1), характеризующая величину запаздывания импульса напряжения;
<1), характеризующая величину запаздывания импульса напряжения;
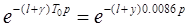 – функция запаздывания;
– функция запаздывания;
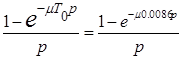 – функция длительности импульса напряжения.
– функция длительности импульса напряжения.
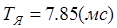 – постоянная времени якорной цепи двигателя.
– постоянная времени якорной цепи двигателя.
Постоянная времени цепи якоря 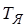 , определяется по формуле:
, определяется по формуле:
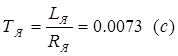 , (3.4)
, (3.4)
где 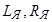 – суммарные значения индуктивностей и сопротивлений обмотки якоря электродвигателя, трансформатора, уравнительных реакторов и дросселя, соединительных проводов и силовой цепи преобразователя.
– суммарные значения индуктивностей и сопротивлений обмотки якоря электродвигателя, трансформатора, уравнительных реакторов и дросселя, соединительных проводов и силовой цепи преобразователя.
Учитывая, что передаточная функция якорной цепи введена в передаточную функцию формирователя тока, в структуре двигателя (рисунок 3.2) остается лишь звено, описывающее электромеханическую часть двигателя:
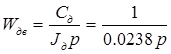 . где
. где 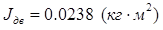 . (3.5)
. (3.5)
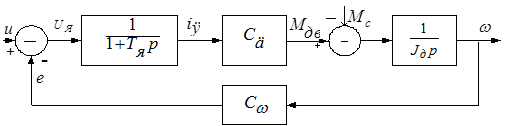
Рисунок 3.2 – Структурная схема двигателя постоянного тока
В качестве датчиков скорости применяются устройства, инерционность которых неизмеримо мала по сравнению с периодом дискретности. Поэтому они могут быть представлены пропорциональным звеном с передаточной функцией:
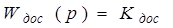 . (3.6)
. (3.6)
С учетом изложенного передаточная функция приведенной неизменяемой части приобретает вид:
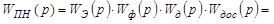 (3.7)
(3.7)
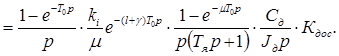 (3.8)
(3.8)
Произведя преобразования, получим:
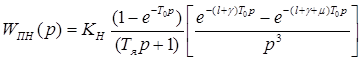 , (3.9)
, (3.9)
где 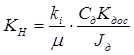 – коэффициент передачи неизменяемой части.
– коэффициент передачи неизменяемой части.
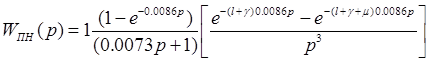
Коэффициент 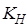 может быть принят равным единице, так как обычно диапазоны управляющих воздействий и сигналов обратной связи одинаковы, (разрядность кода управления
может быть принят равным единице, так как обычно диапазоны управляющих воздействий и сигналов обратной связи одинаковы, (разрядность кода управления 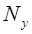 равна разрядности кода обратной связи
равна разрядности кода обратной связи 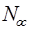 ).
).
Для выполнения синтеза цифрового регулятора неизменяемая часть должна быть представлена дискретными функциями.
Определим дискретную передаточную функцию (ДПФ) приведенной неизменяемой части:
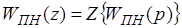 . (3.10)
. (3.10)
При этом следует иметь в виду, что в описании неизменяемой части имеются элементы запаздывания вида 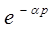 , для которых следует применять модифицированное
, для которых следует применять модифицированное 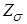 -преобразование.
-преобразование.
Тогда выражение (3.10) принимает вид:
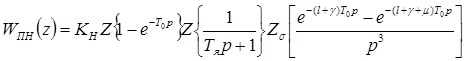 .(3.11)
.(3.11)
В этом выражении 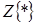 – оператор
– оператор 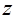 -преобразования без запаздывания, а
-преобразования без запаздывания, а 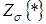 – оператор модифицированного
– оператор модифицированного 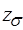 -преобразования (с запаздыванием).
-преобразования (с запаздыванием).
3. Выполнив 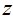 -преобразования получим выражение
-преобразования получим выражение
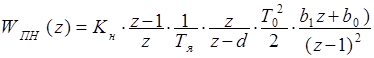 . (3.12)
. (3.12)
Где
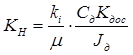 – коэффициент передачи неизменяемой части;
– коэффициент передачи неизменяемой части;
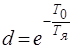 ;
;
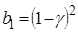 ;
;
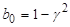 .
.
Коэффициент 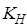 может быть принят равным единице, так как обычно диапазоны управляющих воздействий и сигналов обратной связи одинаковы, (разрядность кода управления
может быть принят равным единице, так как обычно диапазоны управляющих воздействий и сигналов обратной связи одинаковы, (разрядность кода управления 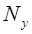 равна разрядности кода обратной связи
равна разрядности кода обратной связи 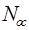 ).
).
Произведя сокращения, получим ДПФ неизменяемой части привода:
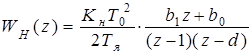 . (3.13)
. (3.13) 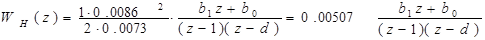
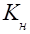 =1,
=1, 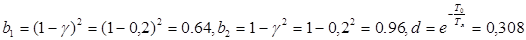
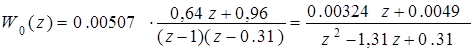
С помощью программного пакета MatLab Simulik можна исследовать поведение САУ ЕП в переходных режимах при налички или отсутствии возбуждающих действий.
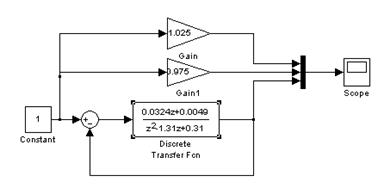
Рисунок 3.3 – Структурная схема неизменяемой части двигателя постоянного тока в Simulik
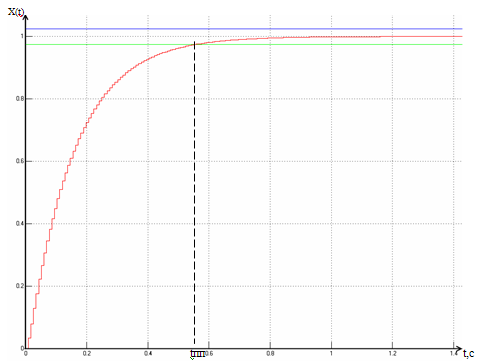
Рисунок 3.3 –График переходного процесса.
Как видно из графика время переходного процесса не отвечает заданым критериям, а поэтому необходимо использовать регулятор для улучшения скорости.
Определение ДПФ неизменяемой части привода позволяет перейти к синтезу регулятора.
Так как синтез регулятора привода целесообразно проводить в частотной области, то дискретную передаточную функцию следует преобразовать в дискретную частотную характеристику (ДЧХ) с помощью билинейного  -преобразования
-преобразования 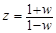 , где
, где 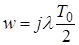 .
.
Для перехода к ДЧХ необходимо в выражении (4.22) произвести подстановку:
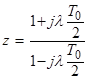 . (3.14)
. (3.14)
Таким образом, в результате преобразований дискретная частотная характеристика неизменяемой части электропривода постоянного тока с широтно-импульсным преобразователем и фотоэлектрическим датчиком скорости равна:
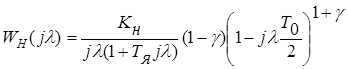 . (3.15)
. (3.15)
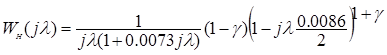
Здесь выражение 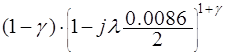 представляет собой характеристику запаздывания управляющего воздействия, а
представляет собой характеристику запаздывания управляющего воздействия, а 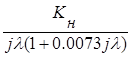 является описанием частотных параметров неизменяемой части привода.
является описанием частотных параметров неизменяемой части привода.
4. СИНТЕЗ РЕГУЛЯТОРА ПРИВОДА ПОСТОЯННОГО ТОКА
При синтезе параметрического регулятора необходимо желаемую ДЧХ разделить на ДЧХ неизменяемой части без учета запаздываний 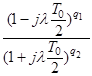 .
.
Тогда ДЧХ параметрического регулятора определяется соотношением:
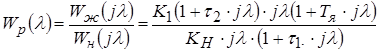 . (4.1)
. (4.1)
В результате сокращения 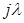 и замены
и замены 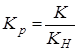 ДЧХ регулятора принимает следующий вид:
ДЧХ регулятора принимает следующий вид:
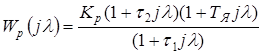 . (4.2)
. (4.2)
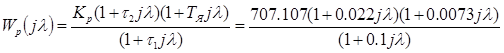
Для перехода от ДЧХ к ДПФ произведем подстановку:
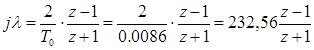 . (4.3)
. (4.3)
После этого ДПФ регулятора принимает следующий вид:
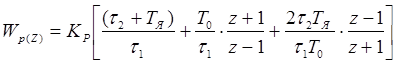 . (4.5)
. (4.5)
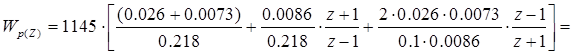
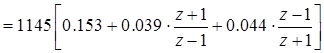 .
.
Полученное выражение ДПФ представляет собой сумму передаточных функций пропорционального, интегрирующего и дифференцирующего звеньев, коэффициенты которых равны:
− пропорционального звена
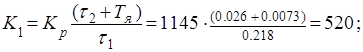 (4.7)
(4.7)
− интегрирующего звена
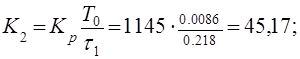 (4.8)
(4.8)
− дифференцирующего звена
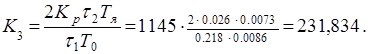 (4.9)
(4.9)
где 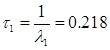 ,
, 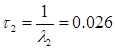 .
.
Структурная схема ПИД-регулятора представлена на рисунке 4.1.
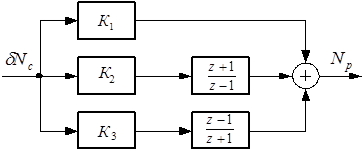
Рисунок 4.1 – Структурная схема цифрового ПИД-регулятора
Функциональная модель привода постоянного тока и ПИД регулятора показана на рисунке 4.2.
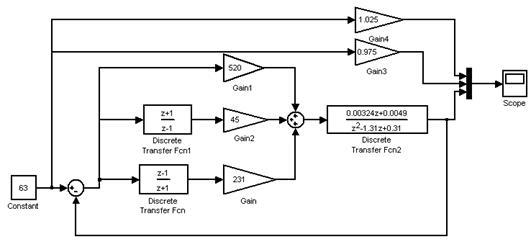
Рисунок 4.2 – Модель системы для оценки ошибки по скорости
При рассчитанных коэффициентах ПИД-регулятора данная система имеет переходный процесс, изображенный на рисунке 4.3.
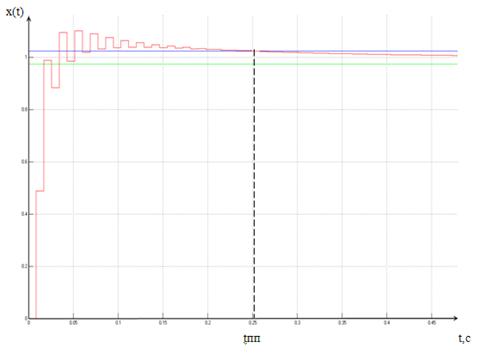
Рисунок 4.3 – График переходной процесса системы с ПИД-регулятором
Как видно из рисунка 4.3, разработанная система удовлетворяет требованиям по быстродействию и точности. Время переходного процесса составляет: tпп = 0,08с.
Программная реализация регулятора требует преобразования ДПФ в разностную форму. С этой целью ДПФ регулятора приводится к общему знаменателю:
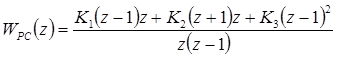 ; (4.10)
; (4.10)
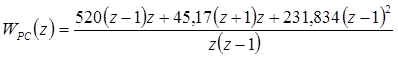 .
.
Сгруппировав переменные, а также умножив числитель и знаменатель на 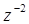 , получим:
, получим:
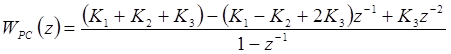 ; (4.11)
; (4.11)
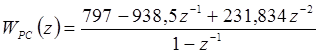 .
.
Применяя обратное z-преобразование, получим разностную форму алгоритма регулятора скорости:
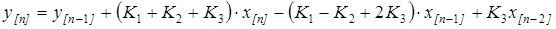 ,(4.13)
,(4.13)
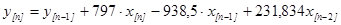 ,
,
где переменные с индексами 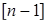 и
и 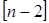 представляют собой предыдущие значения сигналов в периоды дискретности, смещенные на один и два шага относительно текущего периода [
представляют собой предыдущие значения сигналов в периоды дискретности, смещенные на один и два шага относительно текущего периода [ 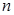 ].
].
Дата: 2019-05-29, просмотров: 332.
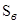 , мм
, мм