Цель: определить уровень развития у учащихся способности оперировать в мышлении пространственными образами.

Ход выполнения. Учитель предлагает школьникам на внеклассном занятии (в ходе викторины, конкурса) или на уроке решать задачи на сообразительность, не требующие каких-либо громоздких вычислений, рассуждений. Задачи могут быть трех типов.

I тип - «Движение». Особенность этих задач состоит в том, что они требуют от школьника умения совершать такие мысленные преобразования, операции, ко­торые видоизменяют лишь местоположение имеющихся у него в представлении образов, перемещают их, но не затрагивают их структурных (композиционных) особенностей. Примерами таких задач могут служить такие:

1) Укажите несколько букв (слов), запись которых имеет ось симметрии (д, ж, м, н, о, п, т, ф, х, ш; топот доход, потоп, поп, тот и др.).

2) Сейчас 2 часа 45 минут. Сколько будет времени» когда минутная стрелка повернется на 210 градусов? (3 часа 20 минут.)

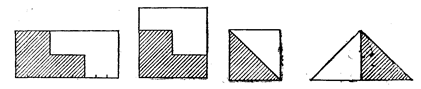
II тип - «Реконструкция». При решении задач этого типа меняется не только местоположение имеющегося в представлении образа, но и его структура, строение. Например, учащимся предлагается разрезать прямоугольник со сторонами 4 и 9 ед. на две равные части таким образом, чтобы, сложив их надлежащим образом, получить квадрат. (Решение показано на рис. 1.)

Еще пример: в квадрате через верхнюю левую вершину провели диагональ. Нижний треугольник оставили на месте, а верхний повернули вокруг этой вершины против часовой стрелки на 270 градусов. Какая фигура образовалась в результате преобразования? (Решение показано на рис. 2.)

В указанных случаях изменилось не только местоположение образа, но и объект оперирования, его структура: был прямоугольник - стал квадрат, был квадрат - стал равнобедренный треугольник.

Ill тип—«Композиция». Решение этих задач требует умения от школьника изменять образ и по местоположению, и по структуре одновременно и неоднократно совершать не одномоментные отдельные операции, а их композиции. Примерами таких задач могут быть следующие:

1) Змея заглатывает свой хвост и проталкивает его внутрь. Чем закончится этот процесс? (Ответ: змея свернется в кольцо без просвета, при этом в сечении у нее будет несколько слоев.)

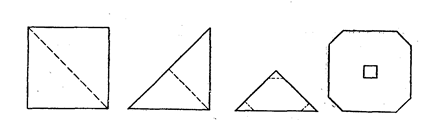
2) Квадратный лист сложили вдвое по диагонали, затем еще раз вдвое так, что получился равнобедренный треугольник. Какая образуется фигура, если каждую вершину последнего треугольника отрезать по линии одинаковой длины, параллельной его противоположным сторонам, и развернуть лист? (Решение показано на рис. 3.)

Ученику предлагают решать задачи всех трех типов начиная с третьего.

Обработка полученных данных. Решение задач определенного типа (первого, второго, третьего) соответствует определенному уровню развития пространственного мышления. Третий уровень - самый высокий. Поэтому, если ученик решил задачу на третий тип оперирования (т. е. обладает третьим уровнем развития пространственного мышления), то более простые задачи второго и первого типа ему уже можно не предлагать. Если он задачу третьего уровня не смог решить, ему предлагают задачу второго уровня. Если и ее он не сможет решить, то дают задачу первого уровня (44), (45), (157).

Мы привели лишь несколько методик для изучения уровня развития познавательных возможностей учащихся. В литературе, приведенной в конце книги, учитель при необходимости найдет и много других методик.

Следует заметить, что почти каждая методика исследования уровня развития тех или иных психических процессов может служить и для их развития. Так, например, если ученик будет достаточное время упражняться в работе по переключению внимания, то его соответствующая способность будет постепенно развиваться и совершенствоваться.

III.4. Изучение особенностей восприятия