Ведущая функция потока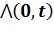 
-математическое ожидание числа вызовов в промежутке 
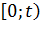. Данная функция: неотрицательная, неубывающая, в практических задачах ТТ непрерывна, принимает только конечные значения.
Средняя интенсивность потока вызова в промежутке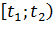 
- есть математическое ожидание числа вызовов в этом промежутке в единицу времени т.е.
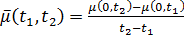. (2.1)
Мгновенная интенсивность определяется выражением:
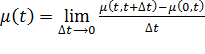.(2.2)
Для стационарного потока, ведущая функция за промежуток времени 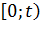равна интенсивности потока т.е.:
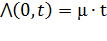. (2.3)
Следовательно, интенсивность стационарного потока есть математическое ожидание числа вызовов, поступающих единицу времени. Чаще всего за единицу времени выбирается средняя длительность одного занятия.
Параметр потока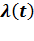 
- в момент времени t,есть предел отношения вероятности поступления не менее одного вызова в промежутке времени 
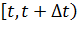к величине этого промежутка 
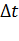если 
:
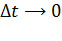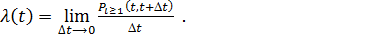(2.4)
Для ординарных потоков существует равенство: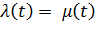 
Для стационарных потоков параметр потока не зависит от времени: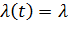 
, таким образом, для случайного потока, обладающего свойствами стационарности и ординарности можно записать:
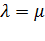. (2.5)
Простейший поток вызовов
Случайный поток вызовов, одновременно обладающий свойствами стационарности, ординарности и отсутствием последействия называется простейшим. Простейший поток полностью определяется функцией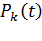 
и подчиняется законам Пуассона:
(2.6)
Пуассоном на основании формулы (2.6) составлены таблицы, которые позволяют определить вероятность поступления не менее k-вызовов за время :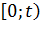
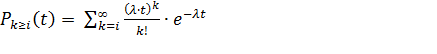(2.7)
Из формул (2.6) и (2.7) видно, что при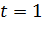 
у.е.в.(условная единица времени) вероятност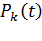и и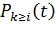 
зависят только от 
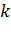и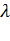 
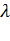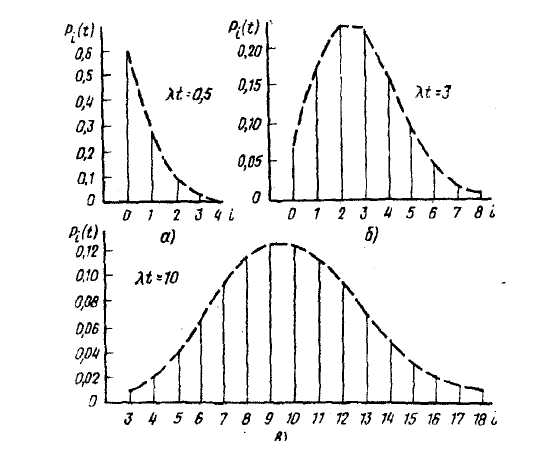
. С возрастанием закон Пуассона стремиться к нормальному закону распределения непрерывной случайной величины (при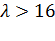 
совпадают с нормальным законом распределения случайной величины). На рис. 2.2 показаны изменения 
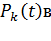зависимости от значения 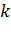и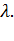 
|
|
Рис. 2.2 – Зависимость 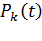от значения 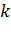и .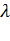
Из рисунков видно, что максимум 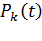достигается:
1. При целом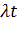 
в двух точках 
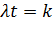и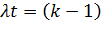 
;
2. При дробном 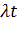в одной точке когда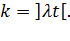 
Свойства простейшего потока
1.При объединении «n» независимых простейших потоков с параметрами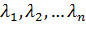 
образуется общий простейший поток с параметром:
Вероятность поступления точно 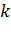вызовов за время 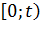определяется формулой Пуассона, а параметр потока формулой (2.8).
2.Сумма вероятностей всех возможных значений числа поступающих вызовов за промежуток времени 
равна единице:
3.Математическое ожидание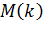 
и дисперсия 
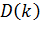числа вызовов за промежуток времени 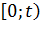совпадают и равны:
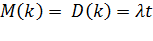(2.10)
Таким образом, для простейшего потока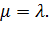 
Примитивный поток вызовов
Случайный ординарный поток вызовов параметр, которого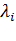 
- прямо пропорционален числу свободных источников нагрузки в данный момент времени называется примитивным:
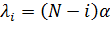, (2.11)
где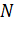 
–общее число источников вызовов;
–число занятых источников;
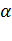-параметр источника в свободном состоянии.
Примитивный поток, часто называют Пуассоновским потоком 2-го рода (простейший – Пуассоновским пот оком 1-го рода), или Энгсетовским.
Примитивный поток является более общим понятием по сравнению с простейшим потоком и переходит в простейший при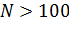 
.
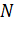Математической моделью примитивного потока вызовов является распределение Бернулли - вероятность поступления вызовов за время t от источников:
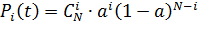, (2.12)
где-интенсивность нагрузки от одного источника:
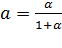. (2.13)
Время обслуживания
Время обслуживания поступившего вызова может быть фиксированным или случайным. Фиксированное время задается последовательностью величин h k, характеризующих длительность обслуживания k-ого вызова или k-ой группы вызовов.Время обслуживания будет постоянным, если h kравно какой-то величине h .
Случайная длительность обслуживания вызова задается функцией распределения соответствующей случайной величины. Самым простым и наиболее распространенным является распределительный закон:
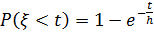, (2.14)
Где h - математическое ожидание времени обслуживания.
Выбор показательного закона распределения объясняется тем, что он обладает свойствами полного отсутствия последействия.
С целью упрощения математических выражений часто за единицу измерения длительности обслуживания принимается математическое ожидание длительности обслуживания, т.е. h=1 у.е.в.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
2.1.Какой поток называется детерминированным?
2.2.Чем может быть определен (задан) детерминированный поток вызовов?
2.3.Чем может быть определен (задан) случайный поток вызовов ?
2.4.Что означает понятие «стационарность потока» ?
2.5.Дайте определение понятия «ординарность потока».
2.6. Что означает понятие «поток с последействием» ?
2.7. Что определяет интенсивность потока вызовов?
2.8.Что определяет параметр потока вызовов ?
2.9.Дайте определение простейшего потока вызовов.
2.10.Какой поток вызовов называется примитивным ?
2.11.Какой поток вызовов называется простейшим?
2.12.Что позволяет определить формула ?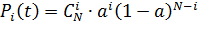
2.13.Что позволяет определить формула первого распределения Эрланга?
2.14.Что позволяет определить первая формула Эрланга?
Дата: 2019-05-29, просмотров: 220.
