ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Поволжский государственный университет телекоммуникаций и информатики»
Кафедра «Автоматической электросвязи»
«Утверждаю»
Зав.кафедрой АЭС, д.т.н.,профессор
_________ А.В.Росляков
«30» августа 2017г .
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине «Теория телетрафика»
для студентов заочного отделения направления подготовки
11.03.02 - Инфокоммуникационные технологии и системы связи
профиль подготовки
Оптические и проводные сети и системы связи
Обсуждено
на заседании кафедры АЭС
«30» августа 2017г.
Протокол №1
2017 г.
Самара
УДК 621.391
Сутягина Л.Н.
«Теория телетрафика». Конспект лекции. – Самара:ПГУТИ,2017.- 65 с.
В курсе «Теория телетрафика» изучаются методы анализа и расчета
пропускной способности телекоммуникационных систем и сетей различной
структуры. Рассматриваются методы исследования вероятностно-временных
характеристик сетей связи и систем коммутации, а также перспективные
методы анализа и синтеза систем телетрафика.
В результате освоения материалов курса студенты получают практические навыки расчета телекоммуникационных систем и сетей.
Рецензент:
Карташевский В.Г. -д.т.н., профессор кафедры «МСИБ» ГОУВПО ПГУТИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Поволжский государственный университет телекоммуникаций и информатики»
Сутягина Л.Н.,2017
Содержание
| Раздел 1Предмет и задачи курса ТТ…………………………………………… | 5 | ||
| 1.1 | Введение в курс Теория телетрафика…………………………………. | 5 | |
| 1.2 | Математический аппарат Теории телетрафика………………………. | 7 | |
| 1.3 | Основные термины Теории телетрафика……………………………… | 8 | |
| Раздел 2Потоки вызовов, свойства, характеристики………………………….. | 11 | ||
| 2.1 | Потоки вызовов…………………………………………………………. | 11 | |
| 2.2 | Основные свойства потоков вызовов…………………………………... | 12 | |
| 2.3 | Основные характеристики потоков вызовов…………………………. | 13 | |
| 2.4 | Простейший поток вызовов…………………………………………… | 14 | |
| 2.5 | Примитивный поток вызовов………………………………………….. | 15 | |
| 2.6 | Время обслуживания…………………………………………………… | 16 | |
| Раздел 3 Телефонная нагрузка. Методы распределения …………………… | 17 | ||
| 3.1 | Телефонная нагрузка…………………………………………………… | 17 | |
| 3.2 | Параметры телефонной нагрузки…………………………………….. | 18 | |
| 3.3 | Методы распределения телефонной нагрузки ……………………… | 21 | |
| Раздел 4 Концепция качества обслуживания в сетях электросвязи…………… | 24 | ||
| 4.1 | Алгоритмы обслуживания вызовов…………………………………… | 24 | |
| 4.2 | Характеристики качества обслуживания……………………………… | 28 | |
| 4.3 | Оценка качества телефонной связи…………………………………… | 30 | |
| Раздел 5 Методы расчета однозвенных полнодоступных включений в системах с явными потерями ………………………………………… | 38 | ||
| 5.1 | Методы расчета однозвенных полнодоступных включений в системах с явными потерями и простейшим потоком вызовов……. | 38 | |
| 5.2 | Методы расчета однозвенных полнодоступных включений в системах с явными потерями и примитивным потоком вызовов…… | 42 | |
| Раздел 6Методы расчета неполнодоступных включений…………………… | 45 | ||
| 6.1 | Неполнодоступные однозвенные включения………………………… | 45 | |
| 6.2 | Методы расчета двухзвенных схем…………………………………… | 46 | |
| Раздел 7 Системы с ожиданием………………………………………………… | 49 | ||
| 7.1 | Методы расчета однозвенных схем в системе с ожиданием………… | 49 | |
| Раздел 8 Методы расчета систем с повторными вызовами……………………. | 53 | ||
| 8.1 | Характеристики качества обслуживания СПВ………………………. | 53 | |
| Раздел 9 Имитационное моделирование процессов обслуживания вызовов… | 57 | ||
Раздел 10Качество обслуживания в сетях с коммутацией пакетов…………. | 59 | ||
| 10.1 | Особенности расчета сетей с пакетной коммутацией………………… | 59 | |
| 10.2 | Анализ межконцевых задержек……………………………………….. | 59 | |
РАЗДЕЛ 1 ПРЕДМЕТ И ЗАДАЧИ КУРСА ТТ
РАЗДЕЛ 2 ПОТОКИ ВЫЗОВОВ, СВОЙСТВА, ХАРАКТЕРИСТИКИ
Потоки вызовов
Поток вызовов – это совокупность моментов поступления вызовов во времени, различают:
- детерминированный поток;
- случайный поток.
Детерминированный поток вызовов (ДП) –представляет поток вызовов, последовательность моментов поступления которых, определена заранее. ДП редко встречается на практике, т.к. сложно обеспечить четкое поступление вызовов по заранее известному расписанию.
Примером ДП могут служить потоки моментов начала и окончания передач программ радио и телевещания по канала связи. Поток сеансов связи с искусственными спутниками земли.
.Однако и здесь возможны случайные, непредвиденные изменения расписания. ДП задается одним из следующих эквивалентных способов (рис.2.1).:
1. Последовательностью моментов поступления вызовов (рис.2.1а) -
 , где k- порядковый номер вызова;
, где k- порядковый номер вызова;
2. Последовательностью промежутков между моментами поступления вызовов (рис.2.1а) - 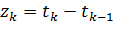 -это промежуток времени предшествующий появлению -го вызова (
-это промежуток времени предшествующий появлению -го вызова ( 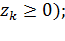
3.Целочисленной неотрицательной и неубывающей функцией 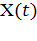 , характеризующей число вызовов, поступивших в промежутке
, характеризующей число вызовов, поступивших в промежутке 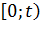 .
.
Точки скачков функции 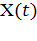 соответствуют моментам поступления вызовов, а величины скачков - числу вызовов, поступивших в вызывающий момент (рис.2.1 б).
соответствуют моментам поступления вызовов, а величины скачков - числу вызовов, поступивших в вызывающий момент (рис.2.1 б).
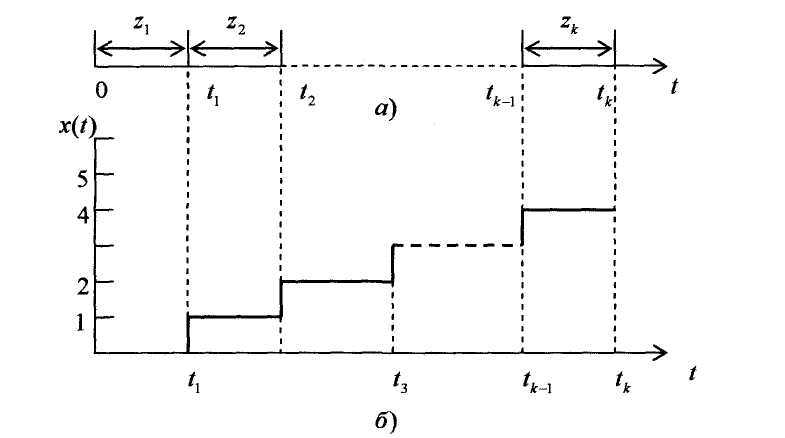
Рис. 2.1 – Способы задания детерминированного потока
Вызывающий момент – это момент времени, в который поступает один или несколько вызовов.
Случайный поток (СП) – это поток вызовов, в котором моменты поступления вызовов и промежутки времени между вызовами являются случайными величинами, поэтому СП задается вероятностным значением распределения соответствующих случайных величин:
1.Законом распределения моментов поступления вызовов 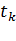 .
.
2.Законом распределения промежутков между линиями 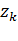 .
.
3.Законом распределения числа поступающих вызовов в промежутке 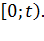
Простейший поток вызовов
Случайный поток вызовов, одновременно обладающий свойствами стационарности, ординарности и отсутствием последействия называется простейшим. Простейший поток полностью определяется функцией 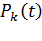 и подчиняется законам Пуассона:
и подчиняется законам Пуассона:
 (2.6)
(2.6)
Пуассоном на основании формулы (2.6) составлены таблицы, которые позволяют определить вероятность поступления не менее k-вызовов за время 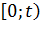 :
:
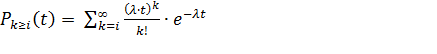 (2.7)
(2.7)
Из формул (2.6) и (2.7) видно, что при 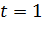 у.е.в.(условная единица времени) вероятности
у.е.в.(условная единица времени) вероятности 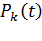 и
и 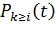 зависят только от
зависят только от 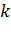 и
и 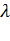 . С возрастанием
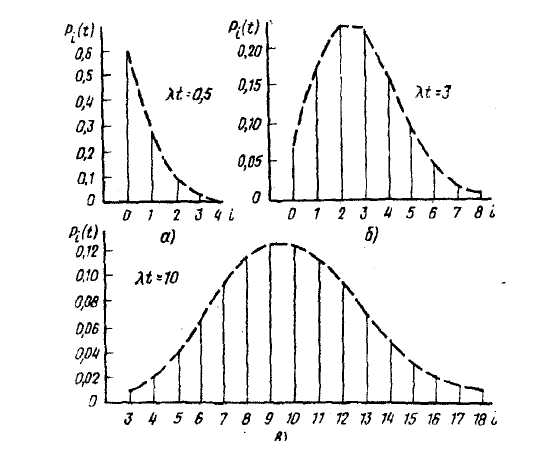
. С возрастанием 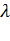 закон Пуассона стремиться к нормальному закону распределения непрерывной случайной величины (при
закон Пуассона стремиться к нормальному закону распределения непрерывной случайной величины (при 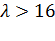 совпадают с нормальным законом распределения случайной величины). На рис. 2.2 показаны изменения
совпадают с нормальным законом распределения случайной величины). На рис. 2.2 показаны изменения 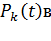 зависимости от значения
зависимости от значения 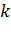 и
и 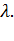
|
|
Рис. 2.2 – Зависимость 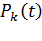 от значения
от значения 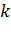 и
и 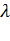 .
.
Из рисунков видно, что максимум 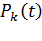 достигается:
достигается:
1. При целом 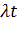 в двух точках
в двух точках 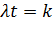 и
и 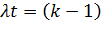 ;
;
2. При дробном 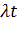 в одной точке когда
в одной точке когда 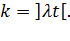
Свойства простейшего потока
1.При объединении «n» независимых простейших потоков с параметрами 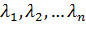 образуется общий простейший поток с параметром:
образуется общий простейший поток с параметром:

Вероятность поступления точно 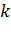 вызовов за время
вызовов за время 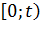 определяется формулой Пуассона, а параметр потока формулой (2.8).
определяется формулой Пуассона, а параметр потока формулой (2.8).
2.Сумма вероятностей всех возможных значений числа поступающих вызовов за промежуток времени  равна единице:
равна единице:

3.Математическое ожидание 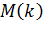 и дисперсия
и дисперсия 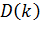 числа вызовов за промежуток времени
числа вызовов за промежуток времени 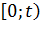 совпадают и равны:
совпадают и равны:
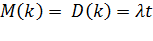 (2.10)
(2.10)
Таким образом, для простейшего потока 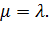
Примитивный поток вызовов
Случайный ординарный поток вызовов параметр, которого 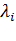 - прямо пропорционален числу свободных источников нагрузки в данный момент времени называется примитивным:
- прямо пропорционален числу свободных источников нагрузки в данный момент времени называется примитивным:
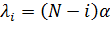 , (2.11)
, (2.11)
где 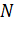 –общее число источников вызовов;
–общее число источников вызовов;
 –число занятых источников;
–число занятых источников;
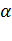 -параметр источника в свободном состоянии.
-параметр источника в свободном состоянии.
Примитивный поток, часто называют Пуассоновским потоком 2-го рода (простейший – Пуассоновским пот оком 1-го рода), или Энгсетовским.
Примитивный поток является более общим понятием по сравнению с простейшим потоком и переходит в простейший при 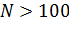 .
.
Математической моделью примитивного потока вызовов является распределение Бернулли - вероятность поступления  вызовов за время t от
вызовов за время t от 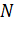 источников:
источников:
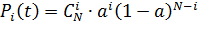 , (2.12)
, (2.12)
где-интенсивность нагрузки от одного источника:
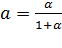 . (2.13)
. (2.13)
Время обслуживания
Время обслуживания поступившего вызова может быть фиксированным или случайным. Фиксированное время задается последовательностью величин h k, характеризующих длительность обслуживания k-ого вызова или k-ой группы вызовов.Время обслуживания будет постоянным, если h kравно какой-то величине h .
Случайная длительность обслуживания вызова задается функцией распределения соответствующей случайной величины. Самым простым и наиболее распространенным является распределительный закон:
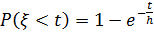 , (2.14)
, (2.14)
Где h - математическое ожидание времени обслуживания.
Выбор показательного закона распределения объясняется тем, что он обладает свойствами полного отсутствия последействия.
С целью упрощения математических выражений часто за единицу измерения длительности обслуживания принимается математическое ожидание длительности обслуживания, т.е. h=1 у.е.в.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
2.1.Какой поток называется детерминированным?
2.2.Чем может быть определен (задан) детерминированный поток вызовов?
2.3.Чем может быть определен (задан) случайный поток вызовов ?
2.4.Что означает понятие «стационарность потока» ?
2.5.Дайте определение понятия «ординарность потока».
2.6. Что означает понятие «поток с последействием» ?
2.7. Что определяет интенсивность потока вызовов?
2.8.Что определяет параметр потока вызовов ?
2.9.Дайте определение простейшего потока вызовов.
2.10.Какой поток вызовов называется примитивным ?
2.11.Какой поток вызовов называется простейшим?
2.12.Что позволяет определить формула 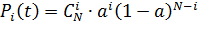 ?
?
2.13.Что позволяет определить формула первого распределения Эрланга?
2.14.Что позволяет определить первая формула Эрланга?
Телефонная нагрузка
Термин «нагрузка»- чаще всего используется специалистами по телефонии и является термином - синонимом «трафика».
Нагрузка - случайный процесс, определяемый числом поступающих вызовов и временем обслуживания каждого вызова. В ТТ используют следующие понятия нагрузки :
1.Поступающая или возникающая нагрузка ( 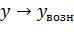 ). Под поступающей
). Под поступающей
на коммутационную систему за промежуток времени 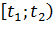 нагрузкой понимается такая нагрузка, которая была бы быть обслужена коммутационной системой, если бы каждому поступающему вызову было бы сразу предоставлено соединение со свободным выходом.
нагрузкой понимается такая нагрузка, которая была бы быть обслужена коммутационной системой, если бы каждому поступающему вызову было бы сразу предоставлено соединение со свободным выходом.
2.Пропущенная коммутационной системой за промежуток времени 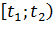 нагрузка
нагрузка 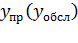 представляет собой сумму времен занятия всех выходов коммутационной системы обслуживающей, поступающий на ее вход поток вызовов за рассматриваемый промежуток времени:
представляет собой сумму времен занятия всех выходов коммутационной системы обслуживающей, поступающий на ее вход поток вызовов за рассматриваемый промежуток времени:
 (3.1)
(3.1)
где V-количество выходов коммутационной системы,
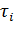 -отрезки времени, в течение которых 1,2,…,
-отрезки времени, в течение которых 1,2,…, 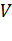 выходов коммутационной системы заняты за время
выходов коммутационной системы заняты за время 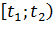 .
.
Из определения пропущенной нагрузки следует свойство аддитивности нагрузки: нагрузка, пропущенная за некоторый промежуток времени равна сумме нагрузок обслуженных на отдельных непересекающихся отрезках времени составляющих этот промежуток, т.е.
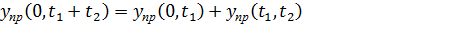 (3.2)
(3.2)
3.Потерянная коммутационной системой нагрузка в течение времен 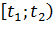 есть разность между поступающей и пропущенной нагрузками за рассматриваемый промежуток времени, т.е.
есть разность между поступающей и пропущенной нагрузками за рассматриваемый промежуток времени, т.е.
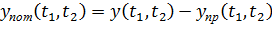 (3.3)
(3.3)
Единицей измерения нагрузки является одночасо-занятие - это такая нагрузка, которая может быть пропущена одной линией, если она будет непрерывно занята в течение часа.
Интенсивность нагрузки - математическое ожидание нагрузки, поступающей в единицу времени.
Единицей измерения интенсивности нагрузки является 1Эрланг – представляет собой нагрузку в одночасо-занятие в час:
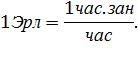
На практике часто используют следующую теорему о количественной оценке интенсивности пропущенной нагрузки: интенсивность пропущенной нагрузки, выраженная в Эрлангах, количественно равна среднему числу одновременно занятых выходов коммутационной системы, обслуживающей эту нагрузку.
Аналогично звучит теорема для интенсивности поступающей нагрузки: интенсивность поступающей нагрузки, создаваемой простейшим потоком вызовов, количественно равна математическому ожиданию числа вызовов, поступающих за время равное средней длительности одного занятия, т.е.
 (3.4)
(3.4)
Нагрузка, как и поток вызовов, подвержена резким колебаниям. Наряду со случайными колебаниями интенсивности нагрузки существуют и периодические (регулярные) колебания, которые учитывают при прогнозировании нагрузки: колебания по дням, неделям, месяцам года, по часам суток
Наиболее значительны колебания нагрузки по часам суток, поэтому введено понятие «час наибольшей нагрузки» (ЧНН) – непрерывный интервал времени в 60 минут в течение, которого средняя интенсивность нагрузки, поступающей на коммутационную систему (узел , является максимальной. Колебание нагрузки в течение суток учитывается коэффициентом концентрации
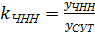 (3.5)
(3.5)
Обычно: 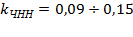
Расчет объема оборудования узлов коммутации, пучков межстанционных линий или каналов осуществляется, исходя из величины нагрузки в ЧНН.
Тип
Абонентской линии
Среднее
Количество
вызовов в ЧНН,С i
Средняя
продолжительность занятия t i ,с
Средняя
Интенсивность исходящей
Время,
Метод НТП для ГТС
Согласно инструкции, изложенной в [6] , расчет интенсивности возникающей абонентской нагрузке при отсутствии статистических данных, должен производиться в соответствии с данными таблицы 7.2 в [6]. Причем расчет возникающей нагрузки, должен производиться отдельно для утреннего и вечернего ЧНН, затем выбирается максимальное значение возникающей нагрузки, которое принимается за расчетную.
В курсовой работе по ТТ и при дипломном проектировании возникающую нагрузку  - ой станции можно определять по формуле
- ой станции можно определять по формуле
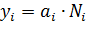 , (3.12)
, (3.12)
где 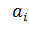 -нагрузка, создаваемая одним абонентом
-нагрузка, создаваемая одним абонентом  - ой категории;
- ой категории;
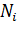 -число абонентов
-число абонентов  - ой категории.
- ой категории.
Например, структурный состав абонентов станции емкостью 15000 номеров: 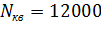 ;
; 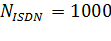 ;
; 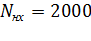 ;
;
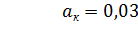 Эрл.
Эрл. 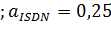 Эрл.;
Эрл.; 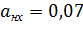 Эрл. , тогда
Эрл. , тогда
 Эрл
Эрл
Методика расчета межстанционных нагрузок изложена в [6], состоит в следующем:
1.Для каждой станции сети определяют возникающую нагрузку, как описано выше, затем определяют
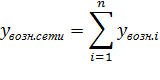
В формуле (3.13) 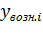 определяется по формуле (3.12). В (3.13) не учитывается нагрузка к ЗТУ.
определяется по формуле (3.12). В (3.13) не учитывается нагрузка к ЗТУ.
2.Определяется в %доля возникающей нагрузки каждой станции в общем возникающем сообщении сети:
 (3.14)
(3.14)
Используя значение 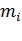 , по таблице 7.3 в [6] определяют долю внутристанционного сообщения, т.е.
, по таблице 7.3 в [6] определяют долю внутристанционного сообщения, т.е. 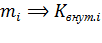
3.Знаязначение 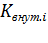 ,определяется величина внутристанционной нагрузки:
,определяется величина внутристанционной нагрузки:
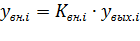 , (3.15)
, (3.15)
где 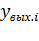 - определяется по формуле (3.9).
- определяется по формуле (3.9).
4.Рассчитывают величину исходящие нагрузки i-ой станции:
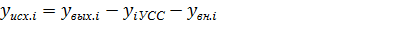 (3.16)
(3.16)
При отсутствии статистических данных нагрузка к узлу спецслужб принимается равным 2% от 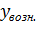 :
:
 (3.17)
(3.17)
5.Интенсивности исходящих нагрузок от каждой станции сети распределяются пропорционально интенсивностям исходящих нагрузок других АТС сети, т.е.:
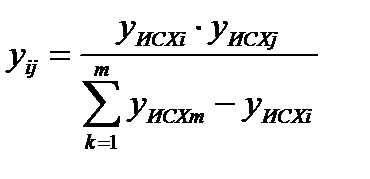 (3.18)
(3.18)
Для определения нагрузки к и от ЗТУ необходимо использовать данные таблицы 7.5 [6], соответственно:
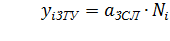
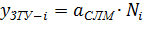 ,
,
где 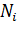 -число абонентов
-число абонентов  -ой станции
-ой станции
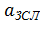 ,
, 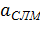 -соответственно нагрузка от одного абонента на ЗСЛ и СЛМ. Данные величины зависят от численности населения города.
-соответственно нагрузка от одного абонента на ЗСЛ и СЛМ. Данные величины зависят от численности населения города.
Вероятность
Потерь по вызовам
ГТС
ОПС-ОПС(РАТС-РАТС)
ОПС-УСС
ОПС- ЗТУ
ЗТУ -ОПС
СТС
ЗТУ -ЦС
ЦС- ЗТУ
ОС-УС
УС-ЦС
ЦС-УС
ОС-ЦС
ЦС-ОС
Для количественной оценки обслуживания вызовов в системах с ожиданием рассчитываются следующие характеристики:
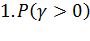 -вероятность ожидания для поступившего вызова (доля задержанных вызовов);
-вероятность ожидания для поступившего вызова (доля задержанных вызовов);
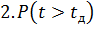 -вероятность ожидания вызова свыше допустимого времени;
-вероятность ожидания вызова свыше допустимого времени;
3.Среднее время ожидания по отношению ко всем поступившим вызовам 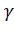 ;
;
4.Среднее время ожидания задержанных вызовов: 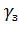 ;
;
5.Средняя длина очереди: 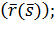
6.Вероятность того, что длина очереди превышает заданную величину 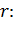
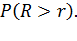
В системе с повторными вызовами рассчитывают следующие характеристики:
1.Вероятность потери первичного вызова: 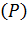 ;
;
2.Вероятность потери повторного вызова: 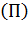 ;
;
3.Вероятность потери любого поступившего вызова: 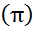 ;
;
4.Вероятность потерь по времени 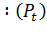 ;
;
5. Вероятность потерь по нагрузке 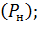
6. Среднее число повторных попыток на установленное соединение: 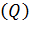 .
.
Для сравнения коммутационных систем по качеству обслуживания часто используют понятие пропускной способности системы: интенсивность пропущенной этой системой нагрузки при заданном качестве обслуживания. Иногда используется величина пропускной способности линии, оцениваемая соотношением:
 (4.4)
(4.4)
В пакетных сетях
При расчете R-фактора одна из составляющих -Is,уменьшающая значение R-фактора, определяется искажениями, возникающими в кодеке при пакетизации речевого сигнала.
Качество передачи речи в сетях с коммутацией пакетов в последние время значительно улучшено путем создания эффективных кодеков, обеспечивающих хорошую разборчивость речевого сигнала на приемном конце.
В состав этих методов входят:
- методы эффективного кодирования речи;
- механизмы подавления пауз (механизм кодирования речи при прерывистой передаче, известный как Voice Activity Detection, VAD);
- механизмы эхоподавления и эхо-компенсации;
- механизмы маскирования ошибок(packet loss concealment), обеспечивающие компенсацию пробелов в речевом потоке, вызванных потерей отдельных пакетов.
В табл. 4.3 представлены характеристики кодеков, реализующих перечисленные выше механизмы повышения качества передачи речи в сетях с коммутацией пакетов.
Кодек G.711 представленных версий имеет скорость выходного сигнала 64 кбит/с, преобразует аналоговый сигнал в цифровой с очень высоким качеством без применения операции сжатия. Однако, при этом требуется значительная пропускная способность по сравнению с кодеками, в которых осуществляется сжатие информации.
Низкоскоростные кодеки требуют существенно меньших значений пропускных способностей, однако оказывают значительно большее влияние на качество речевого сигнала по сравнению с высокоскоростными кодеками.
Таблица 4.3
Типы и характеристики кодеков
| Тип кодека | Скорость передачи, кбит/с | Длительность датаграммы, мс | Задержка пакетизации, мс | Полоса пропускания для двунаправленного соединения, кГц. | Задержка в буфере джиттера | Теоретическая максимальная оценка MOS |
| G.711U | 64 | 20 | 1 | 174,4 | 2 дейтаграммы, 40 мс | 4,4 |
| G.711А | 64 | 20 | 1 | 174,4 | 2 дейтаграммы, 40 мс | 4,4 |
| G.726-32 | 32 | 20 | 1 | 110,4 | 2 дейтаграммы, 40 мс | 4,22 |
| G.729 | 8 | 20 | 25 | 62,4 | 2 дейтаграммы, 40 мс | 4,07 |
| G.723µ | 6,3 | 30 | 67,5 | 43,73 | 2 дейтаграммы, 60 мс | 3,87 |
| G.723А | 5,3 | 30 | 67,5 | 41,6 | 2 дейтаграммы, 60 мс | 3,69 |
Меньшая пропускная способность означает, что можно организовать большее число телефонных соединений по одному и тому же тракту, но при этом уменьшается разборчивость речи, возрастают задержки и качество речи становится более чувствительным к потере пакетов.
Задержка доставки пакета определяется временем переноса пакета от источника до получателя. Время задержки меняется в зависимости от трафика в сети и доступных сетевых ресурсов, в частности, пропускной способности, во время доставки.
Речь представляет собой трафик, чувствительный к задержке, тогда как большинство приложений данных относительно устойчиво к задержке.
Если задержка доставки пакета превышает определенное значение, пакет отбрасывается. Поэтому, при большом числе отброшенных пакетов качество речи ухудшается, что и отражено в формуле (4.6), где влияние задержки учтено через составляющую Id . Необходимо определить, какая задержка допустима при пакетной передаче речи.
В результате исследований качества речевого сигналабыло установлено, что человек начинает чувствовать задержки речевого сигнала, превышающие 150 мс, и ощущает заметный дискомфорт, если задержка превышает 250 мс.
Позднее были проведены масштабные исследования влияния сетевой задержки на качество телефонного разговора, в соответствии с которыми, рекомендуемый порог задержки при передаче речи по пакетной сети равен 150 мс. При задержке 300 мс разговор распадается на фрагменты, которые невозможно связать в слитную речь.
Сквозная задержка доставки пакета D d(«из конца в конец») определяется как сумма четырех составляющих:
D d =Dp+ Dnk+ Dnn + Dbd, (4.7)
где Dp- задержка распространения: время прохождения электрического сигнала в металлическом или волоконно-оптическом кабеле или в беспроводной среде. Это время зависит от физического расстояния между точкой входа и точкой выхода из сети;
Dnk- задержка пакетизации: время, которое необходимо затратить в кодеке для преобразования аналогового сигнала в цифровой и формирования пакета.
Как видно из табл. 4.3, чем ниже скорость сигнала на выходе кодека, тем выше задержка пакетизации, поскольку кодек тратит больше времени на процессы компрессии и декомпрессии сигнала;
Dnn- задержка переноса пакета: время прохождения пакета через все устройства сети, расположенные вдоль пути передачи пакета, включая маршрутизаторы, шлюзы, сетевые экраны, обработчики трафика, сегменты сети с относительно малой пропускной способностью в условиях перегрузки и т. д.
Для некоторых устройств, например, синхронных мультиплексоров, эта величина постоянна, для других, таких, как маршрутизаторы, задержка переноса меняется с изменением нагрузки в сети;
Dbd- задержка на приемной стороне в буфере джиттера: буфер джиттера используется для уменьшения вариаций между моментами поступления пакетов на вход приемного устройства. Буфер может накапливать от одной до нескольких датаграмм.
В соответствии с данными табл. 4.3 типичный буфер джиттера накапливает две датаграммы и задержка Dbd составляет от 20 до 30 мс в зависимости от типа кодека.
Можно сделать вывод, что задержка распространения, задержки в кодеке и буфере джиттера являются постоянными величинами для выбранного пути передачи пакета, тогда как задержка переноса - случайная величина, зависящая от условий в сети в конкретный момент времени.
На рис. 4.8 показано, как задержки влияют на R-фактор и показатели МОS.
Рис. 4.8 - Влияние суммарной задержки на оценки МОS
и величину R-фактора
Для описания случайных изменений между моментами поступления последовательных пакетов речи в приемникиспользуется термин «джиттер» (вариация задержки).
Если моменты прибытия речевых пакетов в пункт назначения становятся нерегулярными, то это ведет к искажению звукового сигнала, и при больших значениях джиттера, превышающих несколько десятков мс, речь становится неразборчивой.
Потери пакетов определяются как процент пакетов, недоставленных к месту назначения. При передаче пакетов по сети возможны следующие причины потери пакета:
- при перегрузке сети очереди в коммутаторах и маршрутизаторах быстро растут. Если перегрузка сохраняется в течение длительного времени, то происходит переполнение буферов и пакеты теряются;
- при наличии ошибок в пакета данных они могут быть переданы повторно в соответствии с запросом приемной стороны, а повторная передача пакетов речи увеличивает задержку пакетов сети. Поэтому при пакетной передаче речи пакеты с ошибками сбрасываются.
Потери речевых пакетов не должны превышать 1% в среднем на достаточно большом временном интервале. При больших значениях коэффициента потерь в восстановленной на приемной стороне речи возникают разрывы.
Таким образом, можно сделать вывод, что метод, основанный на субъективных оценках, используемый в телефонных сетях, не учитывает влияние вероятностно-временных характеристик сетей на качество передачи речи в пакетных сетях.
Главной особенностью Е-модели является то, что этот метод учитывает большой набор факторов, отражающих воздействие оконечных устройств и транспортной среды на качестве обслуживания в пакетной сети. Поэтому метод определения R-фактора, основанный на использовании Е-модели, может рассматриваться, как общая модель для объективной оценки качества передачи речи.
Метод вероятностных графов
Согласно этому методу исследуемая звеньевая схема представляется в виде графа, конфигурация которого зависит от структуры схемы и режима искания, в котором используется схема.
Граф представляет собой картину всевозможных путей между заданным входом схемы и заданным выходом. Дуги графа соответствуют промежуточным линиям или маршрутам и выходам коммутационной системы. Вершины соответствуют точкам коммутации. Таким образом, процедура метода вероятностных графов заключается в том, чтобы записать функцию для вероятности потерь при установлении соединения. Обычно при составлении графа исследуемой системы используются простейшие типовые схемы:
Wi- вероятность занятости дуги, равная интенсивности нагрузки пропущенная линией или маршрутом, который характеризуется этой дугой.
Вероятность потерь в графе, состоящем из α-паралельно
параллельно включенных дуг: 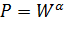
Вероятность потерь в графе, состоящем из -последовательно включенных дуг и вероятностямизанятия этих
дуг: 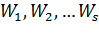 соответственно, определяется выражением:
соответственно, определяется выражением:

Граф типа П:
Рассмотрим пример построения вероятностного графа для различных трехзвенных схем (рис.6.1).
Рис. 6.1 – Вероятностные графы для различных трехзвенных схем
Структура каждого графа отображает возможность пути установления соединений. Если для каждой дуги графа определить вероятность успешного установления пути, то между точками А и В можно определить возможность потери.
Например, для графа (а) на рис. 6.1 используются обозначения:
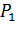 - вероятность успешного создания пути между точками «А» и «2-1»;
- вероятность успешного создания пути между точками «А» и «2-1»;
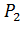 - вероятность успешного создания пути между точками «А» и «2-2»;
- вероятность успешного создания пути между точками «А» и «2-2»;
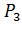 - вероятность успешного создания пути между точками «2-1» и «3»;
- вероятность успешного создания пути между точками «2-1» и «3»;
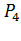 - вероятность успешного создания пути между точками «2-2» и «3»;
- вероятность успешного создания пути между точками «2-2» и «3»;
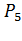 - вероятность успешного создания пути между точками «3» и «В».
- вероятность успешного создания пути между точками «3» и «В».
Тогда вероятность успешного установления пути между точками «А» и «3» будет определяться выражением:
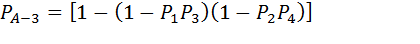 (6.14)
(6.14)
Соответственно, занятость этого пути:
 (6.15)
(6.15)
Тогда искомая вероятность потери вызова между точками А и В будет определятся выражением:
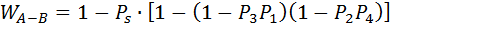 (6.16)
(6.16)
Вероятность, определяемая по формуле (6.16) равна единице при следующих условиях:
1) нет свободных путей между вершинами «3» и «В» (или 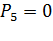 );
);
2) нет свободных путей между вершинами «2-1» и «А», а также между вершинами «2-2» и «3» ( 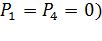 .
.
Анализируя представленный граф, можно сделать вывод, что для рассматриваемой модели наиболее важной является доступность пути между вершинами «3» и «В».
КОНТРОЛЬНЫЕ ВОПРОСЫ:
6.1.Перечислите аналитические методы расчета неполнодоступных включений.
6.2.В чем суть метода вероятностных графов?
6.3.Что представляет собой вероятностный граф?
6.4.Что представляет собой граф типа П?
6.5.Что представляет собой граф типа S?
Тип исходящей
Попытки
Безуспешным
Для расчета СМО с повторными вызовами разработано множество моделей и методов, ориентированных на использование таблиц и/или программных продуктов. Для простых моделей получены аналитические выражения.
Рассмотрим пример такой модели. Полнодоступная коммутационная система имеет 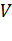 выходов, поступающий первичный поток вызовов - простейший с параметром
выходов, поступающий первичный поток вызовов - простейший с параметром 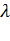 . Время обслуживания любого вызова – случайная величина, распределённая по показательному закону со средним значением единица.
. Время обслуживания любого вызова – случайная величина, распределённая по показательному закону со средним значением единица.
Поток повторных вызовов с параметром 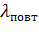 :
:
 (8.2)
(8.2)
где j-число источников повторных вызовов;
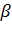 -интенсивность повторения вызова одним источником.
-интенсивность повторения вызова одним источником.
Предположим, что источник, послав первый вызов и получив отказ в соединение, с вероятностью 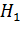 – повторяет его, а с вероятностью
– повторяет его, а с вероятностью 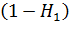 отказывается от дальнейших попыток установления соединения.
отказывается от дальнейших попыток установления соединения.
Аналогично для повторных вызовов обозначим 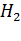 - вероятность повторения повторного вызова,
- вероятность повторения повторного вызова, 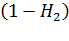 - отказ от повторения повторного вызова.
- отказ от повторения повторного вызова.
Величины 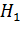 и
и 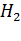 характеризуют меру настойчивости источника вызовов.
характеризуют меру настойчивости источника вызовов.
Состояние коммутационной системы будет определяться двумя параметрами:
 - число занятых выходов коммутационной системы(
- число занятых выходов коммутационной системы( 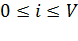 ) ;
) ;
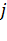 - число источников повторяющихся вызовов(
- число источников повторяющихся вызовов( 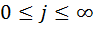 ).
).
Соответственно 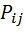 определяет вероятность состояния коммутационной системы в установившемся режиме.
определяет вероятность состояния коммутационной системы в установившемся режиме.
Изменение состояния системы за промежуток времени 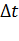 возможно при осуществлении одного из следующих событий:
возможно при осуществлении одного из следующих событий:
1) поступление первичного вызова (вероятность поступления 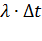 );
);
2) поступление повторного вызова (вероятность поступления 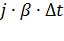 );
);
3) освобождение одного из занятых выходов 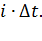
В первом случае число занятых выходов ( 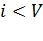 )увеличивается на единицу. Во втором случае, одновременно с увеличением числа занятых выходов, уменьшается на единицу число источников повторных вызовов. В третьем случае уменьшается на единицу число занятых выходов.
)увеличивается на единицу. Во втором случае, одновременно с увеличением числа занятых выходов, уменьшается на единицу число источников повторных вызовов. В третьем случае уменьшается на единицу число занятых выходов.
Если первичный вызов поступит в состоянии 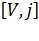 , то источник, получив отказ в соединении, перейдет в число повторяющего вызова с вероятностью
, то источник, получив отказ в соединении, перейдет в число повторяющего вызова с вероятностью 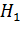 , величина
, величина 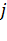 при этом, увеличивается на 1.
при этом, увеличивается на 1.
При поступлении в состоянии 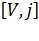 повторяющего вызова с вероятностью
повторяющего вызова с вероятностью 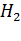 состояние коммутационной системы не изменяется (источник будет продолжать повторение вызовов). Соответственно с вероятностью
состояние коммутационной системы не изменяется (источник будет продолжать повторение вызовов). Соответственно с вероятностью 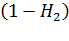 -величина
-величина 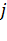 уменьшится на 1, а источник повторяющихся вызовов станет свободным.
уменьшится на 1, а источник повторяющихся вызовов станет свободным.
Для установившегося режима система уравнений вероятностей состояний исследуемой коммутационной системы будет иметь вид:
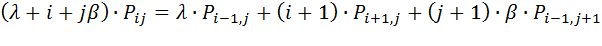 , (8.3)
, (8.3)
где 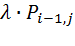 -вероятность поступления нового вызова от источника первичных
-вероятность поступления нового вызова от источника первичных
вызовов;
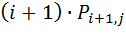 -вероятность освобождения одного выхода;
-вероятность освобождения одного выхода;
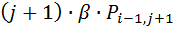 -вероятность поступления нового вызова от источника первичных вызовов и переход его в источник повторных вызовов.
-вероятность поступления нового вызова от источника первичных вызовов и переход его в источник повторных вызовов.
С учетом соответствующих вероятностей 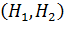 , уравнение (8.3) можно записать в следующем виде:
, уравнение (8.3) можно записать в следующем виде:
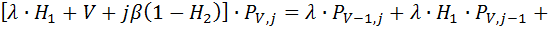
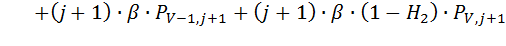 (8.4)
(8.4)
При условиях: 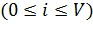 ;(
;( 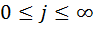 );
); 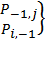 .- не существуют
.- не существуют
По условию нормирования( 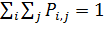 )выражение (8.4) имеет вид:
)выражение (8.4) имеет вид:
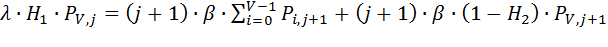 (8.5)
(8.5)
Полученное выражение позволяет определить основные характеристики качества обслуживания.
ОБСЛУЖИВАНИЯ ВЫЗОВОВ
Имитационное или статистическое моделирование процессов обслуживания вызовов на ПЭВМ – это способ математического исследования систем коммутации. Он используется, когда не удается определить характеристики качества обслуживания аналитическими методами или когда требуется сравнить качество обслуживания конкретной коммутационной системой потока вызовов с теоретическими моделями.
При моделировании на ПЭВМ имитируется работа исследуемой коммутационной системы, т.е собирается , обрабатывается и выдается необходимая статистика об имитируемом процессе обслуживания вызовов.
В пределах изучаемой математической модели можно с любой заданной точностью воспроизвести исследуемый процесс и получить интересующие статистические характеристики.
Моделирование начинается с разработки задания на его проведение, где формируется цель и задача предстоящего исследования, определяются требования к точности и объему получаемых результатов.
Особое внимание должно уделяться оптимальному заданию исходных данных, по материалу задания разрабатывается алгоритм и пишется программа моделирования. Так как алгоритм моделирования должен отражать случайную природу имитируемого процесса обслуживания, то в его реализации используются случайные числа и события.
В структуре программы моделирования можно выделить:
a) информационную часть;
б) алгоритмическую часть.
Информационная часть отражает структуру и текущее состояние системы обслуживающей вызовы, содержит сведения о находящихся в системе вызовов и накапливаемых статистических характеристиках.
Алгоритмическая часть – это комплекс алгоритмов в процессе функционирования, которого меняются значения переменных информационной части.
Для имитации случайных величин используют стандартные подпрограммы (датчики) генерирующие псевдослучайные числа, т.е. такие числа, когда каждое число получается из предыдущего в результате применения арифметических или логических операций.
Эти числа называются псевдослучайными а не случайными, т.к. получаемые последовательности чисел являются периодическими. Период последовательности должен быть достаточным для требуемого объема статистических испытаний.
Обычно используют алгоритм для получения равномерно распределенных псевдослучайных величин, а затем, с помощью соответствующих преобразований, получают последовательности чисел с другими функциями распределения.
Для случая равномерного распределения в интервале 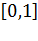 псевдослучайное число
псевдослучайное число 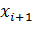 может быть получено из предыдущего числа
может быть получено из предыдущего числа 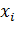 с помощью соотношения:
с помощью соотношения:
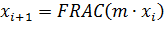 , (9.1)
, (9.1)
где 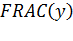 - оператор дробной части от выражения
- оператор дробной части от выражения 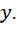
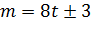 , (9.2)
, (9.2)
где  - нечетное целое число.
- нечетное целое число.
Обычно перед использованием датчика псевдослучайных чисел задается начальное значение 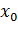 на отрезке
на отрезке 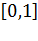 . Задание разных значений
. Задание разных значений 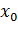 позволяет формировать различные последовательности случайных величин.
позволяет формировать различные последовательности случайных величин.
Рассмотрим пример моделирования процесса обслуживания вызовов коммутационной системой математическая модель, которой 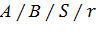 ,
,
где А – тип распределения промежутков между вызовами;
В – тип распределения длительности обслуживания вызово;
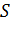 – схема обслуживания;.
– схема обслуживания;.
 –число мест ожиданий. Для систем с явными потерями
–число мест ожиданий. Для систем с явными потерями 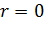 .
.
Обозначим:
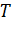 - среднее время обслуживания вызова;
- среднее время обслуживания вызова;
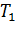 -время поступления очередного вызова;
-время поступления очередного вызова;
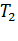 -время окончания обслуживания очередного вызова.
-время окончания обслуживания очередного вызова.
Если 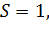 т.е (однолинейная система), то этапы моделирования состоят в следующем:
т.е (однолинейная система), то этапы моделирования состоят в следующем:
1) 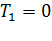
2) Моделируется время окончания обслуживания очередного состояния, учитывая тип распределения длительности обслуживания: 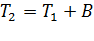 ;
;
3) Моделируется момент поступления очередного вызова, учитывая тип распределения промежутков между вызовами.
4) Выполняется проверка: закончено ли моделирование, что реализуется сравнением 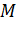 (число поступивших вызовов) и
(число поступивших вызовов) и 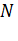 (число вызовов, необходимых для моделирования). Сравнивая,
(число вызовов, необходимых для моделирования). Сравнивая, 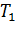 и
и 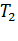 определяют, потерян вызов или обслужен.
определяют, потерян вызов или обслужен.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
9.1.В чем состоит процесс моделирование случайных величин и событий ?
9.2.Из каких частей состоит программа моделирования ?
9.3.Из каких процедур состоит разработка алгоритмов моделирования
процессов обслуживания вызовов в телефонных сетях?
9.4.Составьте алгоритм моделирования процессов обслуживания вызовов в
системах с явными потерями.
9.5.Составьте алгоритм моделирования процессов обслуживания вызовов
в системах с ожиданием.
9.6.Составьте алгоритм моделирования процессов обслуживания вызовов в
системах с повторными вызовами.
КОММУТАЦИЕЙ ПАКЕТОВ
Анализ межконцевых задержек
Для построения модели СМО, описывающей функционирование базовой сети с коммутацией пакетов, которая включает:
-М-каналов передачи данных и - W-узлов коммутации.
Введем ряд упрощающих предположений:
1)предположение о независимости, состоящее в том, что длина пакета, поступающего в канал, выбирается независимо в соответствии с плотностью распределения:
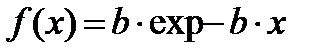 , (10.1)
, (10.1)
где 1/b-средняя длина пакета, измеряемая в битах (или байтах).
Данное предположение позволяет устранить зависимость между временами обслуживания в каналах.
Процесс поступления пакета в сеть является Пуассоновским с параметром
Λr[пак/час]. Здесь r- номер пары «узел источник»-«узел адресат».
Все пары упорядочены в соответствии с номерами 1,2,3,…R . Маршрут пакетов r-ого класса, т.е передаваемых в r-ой паре «источник – адресат», определяется матрицей:
 (10.2),
(10.2),
где 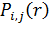 - вероятность того, что пакетr-ого класса, закончивший обслуживание в
- вероятность того, что пакетr-ого класса, закончивший обслуживание в
 - ом канале, поступит потом в
- ом канале, поступит потом в 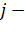 ый канал, причем
ый канал, причем 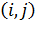 будут принимать значение
будут принимать значение 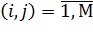 .
.
Различные способы задания матрицы (10.2) определяют тип маршрутизации пакета в базовой сети. Например, при использовании постоянных виртуальных соединений и фиксированной маршрутизации, соответствущие значения для элементов 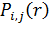 могут принимать лишь два значения – «0» и «1»
могут принимать лишь два значения – «0» и «1»
2) объемы буферных накопителей не ограничены и подтверждение об успешной доставке пакета передается мгновенно.
Сделанные предположения позволяют полностью определить разомкнутую неоднородную СМО,моделирующую функционирование базовой сети передачи данных.
Сеть без источников и стоков (адресатов) называется замкнутой, в противном случае разомкнутой. Если заявки, циркулирующие в сети одного типа, то сеть называется однородной и наоборот.
Более общий случай неоднородной сети: каждый тип сообщения имеет свою функцию распределения длительности обслуживания в каждом УК, а так же свой закон перехода между узлами сети.
В рассматриваемую СМО поступает r- классов пуассоновских потоков пакетов с интенсивностью, 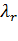 , (причем
, (причем 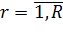 ) маршрут каждого из которых характеризуется матрицей (10.2).
) маршрут каждого из которых характеризуется матрицей (10.2).
Функция распределения длительности обслуживания пакетов r-го класса в
 -ом УК СМО, которая моделирует канал передачи данных,являться экспоненциальной с параметром:
-ом УК СМО, которая моделирует канал передачи данных,являться экспоненциальной с параметром:
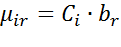 , (10.3)
, (10.3)
где 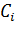 - пропускная способность i-го канала, измеряемая в битах/секунду;
- пропускная способность i-го канала, измеряемая в битах/секунду; 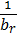 - средняя длина пакета r-го класса.
- средняя длина пакета r-го класса.
Интенсивность потока пакетов r-го класса, поступающих в -ыйканал, - ( 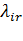 ) удовлетворяет уравнению баланса потоков:
) удовлетворяет уравнению баланса потоков:
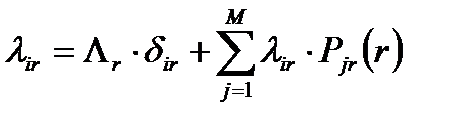 , (10.4)
, (10.4)
где 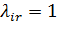 , если входящий поток Λrпоступит в i-ый канал;
, если входящий поток Λrпоступит в i-ый канал;
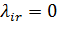 , если входящий поток Λrне поступит в i-ыйканал.
, если входящий поток Λrне поступит в i-ыйканал.
Общий поток пакетов, поступающих в i-ый канал:
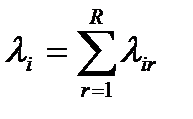 (10.5)
(10.5)
Соответственно, общий поток пакетов,поступающих в сеть:
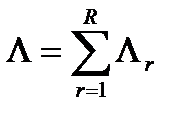 (10.6)
(10.6)
Обозначим загрузку i-го канала пакетами -го классачерез 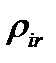 ,а общую загрузкуi-го канала через
,а общую загрузкуi-го канала через 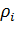 ,тогда
,тогда
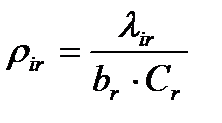 (10.7) ;
(10.7) ;
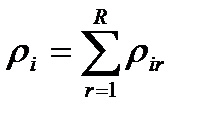 (10.8)
(10.8)
Вероятность стационарного состояния сети P ( n ) определяется выражением: 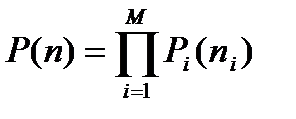 , (10.9)
, (10.9)
где n i– число пакетов, передаваемых по i -ому каналу.
В формуле (10.9) при дисциплине обслуживания FCFS можно записать:
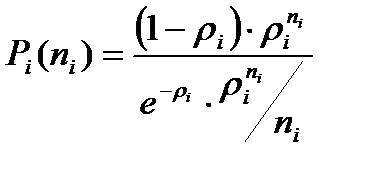 (10.10)
(10.10)
P i (ni) - вероятность i -го состояния сети при числе пакетов, передаваемых по
i -ому каналу - ni.
Предполагая, что передача пакетов по каналу осуществляется в соответствии с
дисциплиной FCFS, можно определить среднее количество пакетов вi - ом канале:
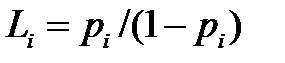 ,
,
тогда среднее число пакетов в сети в целом равно:
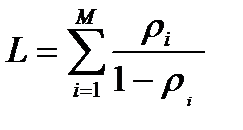 (10.11)
(10.11)
В то же время, в соответствии с формулой Литтласреднее число пакетов в сети:L=( ΛxT), где Т - среднее время пребывания пакета в сети.
Таким образом,
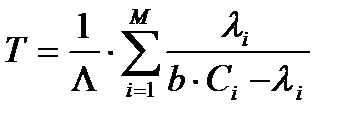 (10.12)
(10.12)
Выражение (10.12) было впервые получено Клейнроком.
Различные методы квитирования и ограниченный объем буферной памяти узла коммутации, оказывает существенное влияние на характеристики базовой сети передачи данных,что должно находить отражение в соответствующих моделях СМО.
Рассмотрим модель гипотетической сети, в которой установлено семь УК(рис. 10.1).
Рис. 10.1 - Модель гипотетической сети
Рассмотрим процесс обмена информацией между УК1 и УК7. Между этими УК установлено 3 пути обмена пакетами, вероятность использования которых определяется величинами 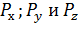 . Очевидно, что сумма этих вероятностей:
. Очевидно, что сумма этих вероятностей:
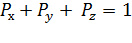
Допустим , что каждый УК обслуживает поступающий поток пакетов по дисциплине с ожиданием. Тогда интенсивность входящего потока можно обозначить
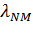 , а интенсивность обработанного потока пакетов -
, а интенсивность обработанного потока пакетов - 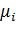 .В соответствии с этими обозначениями рис. 10.1 будет иметь вид:
.В соответствии с этими обозначениями рис. 10.1 будет иметь вид:
Рис. 10.2 - Модель исследуемой сети
Допустим, что каждый УК может быть представлен моделью вида 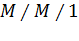 , тогда время прибывания пакета в i-ом коммутаторе определяется по формуле:
, тогда время прибывания пакета в i-ом коммутаторе определяется по формуле:
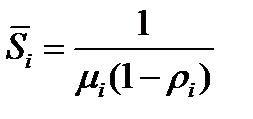 (10.13)
(10.13)
В формуле (10.13) загрузка определяется отношением интенсивности входящего потока к интенсивности обслуженного потока. Например, для УК3загрузка определяется выражением: 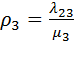 .
.
Средняя задержка пакета на маршруте, выбираемом с вероятностью 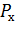 , будет определяться выражением :
, будет определяться выражением :
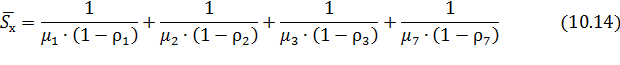
Тогда, с учетом соответствующих вероятностей 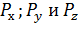 , средняя задержка пакета в сети, представленной на рисунке (10.2), будет определяться выражением:
, средняя задержка пакета в сети, представленной на рисунке (10.2), будет определяться выражением:
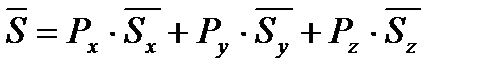 (10.15)
(10.15)
КОНТРОЛЬНЫЕ ВОПРОСЫ:
10.1.Из каких элементов состоит базовая сеть коммутации пакетов?
10.2.В чем состоит основная задача моделирования сетей с КП?
10.3.Перечислите наиболее важные качественные характеристики сетей с КП?
10.4.Какие протоколы используются в сетях с КП и как они влияют на
характеристики сети передачи данных?
10.5.Какая сеть СМО называется разомкнутой?
10.6.Какая сеть СМО называется неоднородной?
10.7.Как определить среднее время пребывания пакета в сети?
10.8.Как определить загрузку узла коммутации пакетной сети?
10.9.Как определить среднюю задержку пакета на маршруте в пакетной сети?
10.10.Как производится расчет вероятности потерь в узле коммутации сети с коммутацией пакетов?
РЕКОМЕНДОВАННАЯ ЛИТЕРАТУРА
Основная литература:
1. Степанов С.Н.Основытелетрафикамультисервисныхсетей.- М.: Эко- Трендз, 2010.
2.Сутягин а Л.Н. Расчет межстанционных связей аналогово-цифровой ГТС/ Учебное пособие. ПГУТИ, 2010.
3. Гольдштейн Б.С., Соколов Н.А., Яновский Г.Г. Сети связи // СПб.: БХВ-2010.
Дополнительная литература:
1. Крылов В.В., Самохвалов С.С. Теория телетрафика и ее приложения.-
Санкт- Петербург.: «БХВ-Петербург », 2005.-287с.
2.Решетников Н.В., Теория телетрафика. Курсовое и дипломное
проектирование. Справочное пособие –М.: Радио и связь,2005.-99 с.
3.Карташевский В.Г.Основы теории массового обслуживания.- М.: Радио и связь, 2006.
4.Корнышев Ю.Н., Пшеничников А.П., ХаркевичА.Д.Теория
телетрафика. – М.: Радио и Связь, 1996 . – 270с.
5.Корнышев Ю.Н., Фань Г.Л. Теория распределения информации.
М.: Радио и связь, 1985. –184с.
6.Нормы технологического проектирования. Городские и сельские
телефонные сети. НТП 112. 2000,РД 45.120-2000. М.: Информсвязь, 2001.
7.Клейнрок Л.Теория массового обслуживания.-М.:Машиностроение,1979.
8.Саати Т.Л.Элементы теории массового обслуживания и её приложения.-М.: Сов.Радио,1965.
9.ITU-D.Teletraffic Engineering Handbook.- Geneva,2003(монография размещена на сайте: http://www.itu/int).
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Поволжский государственный университет телекоммуникаций и информатики»
Кафедра «Автоматической электросвязи»
«Утверждаю»
Зав.кафедрой АЭС, д.т.н.,профессор
_________ А.В.Росляков
«30» августа 2017г .
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине «Теория телетрафика»
для студентов заочного отделения направления подготовки
11.03.02 - Инфокоммуникационные технологии и системы связи
профиль подготовки
Оптические и проводные сети и системы связи
Обсуждено
на заседании кафедры АЭС
«30» августа 2017г.
Протокол №1
2017 г.
Самара
УДК 621.391
Сутягина Л.Н.
«Теория телетрафика». Конспект лекции. – Самара:ПГУТИ,2017.- 65 с.
В курсе «Теория телетрафика» изучаются методы анализа и расчета
пропускной способности телекоммуникационных систем и сетей различной
структуры. Рассматриваются методы исследования вероятностно-временных
характеристик сетей связи и систем коммутации, а также перспективные
методы анализа и синтеза систем телетрафика.
В результате освоения материалов курса студенты получают практические навыки расчета телекоммуникационных систем и сетей.
Рецензент:
Карташевский В.Г. -д.т.н., профессор кафедры «МСИБ» ГОУВПО ПГУТИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Поволжский государственный университет телекоммуникаций и информатики»
Сутягина Л.Н.,2017
Содержание
| Раздел 1Предмет и задачи курса ТТ…………………………………………… | 5 | ||
| 1.1 | Введение в курс Теория телетрафика…………………………………. | 5 | |
| 1.2 | Математический аппарат Теории телетрафика………………………. | 7 | |
| 1.3 | Основные термины Теории телетрафика……………………………… | 8 | |
| Раздел 2Потоки вызовов, свойства, характеристики………………………….. | 11 | ||
| 2.1 | Потоки вызовов…………………………………………………………. | 11 | |
| 2.2 | Основные свойства потоков вызовов…………………………………... | 12 | |
| 2.3 | Основные характеристики потоков вызовов…………………………. | 13 | |
| 2.4 | Простейший поток вызовов…………………………………………… | 14 | |
| 2.5 | Примитивный поток вызовов………………………………………….. | 15 | |
| 2.6 | Время обслуживания…………………………………………………… | 16 | |
| Раздел 3 Телефонная нагрузка. Методы распределения …………………… | 17 | ||
| 3.1 | Телефонная нагрузка…………………………………………………… | 17 | |
| 3.2 | Параметры телефонной нагрузки…………………………………….. | 18 | |
| 3.3 | Методы распределения телефонной нагрузки ……………………… | 21 | |
| Раздел 4 Концепция качества обслуживания в сетях электросвязи…………… | 24 | ||
| 4.1 | Алгоритмы обслуживания вызовов…………………………………… | 24 | |
| 4.2 | Характеристики качества обслуживания……………………………… | 28 | |
| 4.3 | Оценка качества телефонной связи…………………………………… | 30 | |
| Раздел 5 Методы расчета однозвенных полнодоступных включений в системах с явными потерями ………………………………………… | 38 | ||
| 5.1 | Методы расчета однозвенных полнодоступных включений в системах с явными потерями и простейшим потоком вызовов……. | 38 | |
| 5.2 | Методы расчета однозвенных полнодоступных включений в системах с явными потерями и примитивным потоком вызовов…… | 42 | |
| Раздел 6Методы расчета неполнодоступных включений…………………… | 45 | ||
| 6.1 | Неполнодоступные однозвенные включения………………………… | 45 | |
| 6.2 | Методы расчета двухзвенных схем…………………………………… | 46 | |
| Раздел 7 Системы с ожиданием………………………………………………… | 49 | ||
| 7.1 | Методы расчета однозвенных схем в системе с ожиданием………… | 49 | |
| Раздел 8 Методы расчета систем с повторными вызовами……………………. | 53 | ||
| 8.1 | Характеристики качества обслуживания СПВ………………………. | 53 | |
| Раздел 9 Имитационное моделирование процессов обслуживания вызовов… | 57 | ||
Раздел 10Качество обслуживания в сетях с коммутацией пакетов…………. | 59 | ||
| 10.1 | Особенности расчета сетей с пакетной коммутацией………………… | 59 | |
| 10.2 | Анализ межконцевых задержек……………………………………….. | 59 | |
Дата: 2019-05-29, просмотров: 324.