У програмі передбачено обчислення обсягів і площ поверхонь тіл обертання, що утворюють яких обертаються навколо осі Оx або Oy в прямокутній декартовій системі координат і задаються одним з трьох способів:
1. у вигляді явної залежності між змінними x і y: y = f (x);
2. у вигляді заданої параметрично залежності між змінними x і y: x = f (t), y = g (t), де t – мінлива-параметр;
3. у вигляді ламаної, заданої впорядкованим набором вершин у площині xOy.
Відразу після створення об'єкта типу Поверхня обертання розпочнеться обчислення об'єму та площі поверхні тіла, обмеженого поверхнею, утвореної обертанням графіка заданої функції або ламаного. Цей процес вимагає певного часу, тому під час обчислення з'являється вікно з показником стану виконання обчислень.
Після обчислення результат буде виведено у полі характеристик поточного об'єкта. У програмі передбачено обчислення обсягів і площ поверхонь тіл обертання, що утворюють яких обертаються навколо осі Оx або Oy в прямокутній декартовій системі координат і задаються одним з трьох способів:
1. у вигляді явної залежності між змінними x і y: y = f (x);
2. у вигляді заданої параметрично залежності між змінними x і y: x = f (t), y = g (t), де t – мінлива-параметр;
3. у вигляді ламаної, заданої впорядкованим набором вершин у площині xOy.
Відразу після створення об'єкта типу Поверхня обертання розпочнеться обчислення об'єму та площі поверхні тіла, обмеженого поверхнею, утвореної обертанням графіка заданої функції або ламаного. Цей процес вимагає певного часу, тому під час обчислення з'являється вікно з показником стану виконання обчислень.
Після обчислення результат буде виведено у полі характеристик поточного об'єкта.
Обчислення значення вираження.
Під час роботи з програмою іноді виникає необхідність обчислити значення деякого вираження. У таких випадках зручно скористатися послугою Обчислення \ Значення виразу. На вкладці Значення виразу вікна Обчислення, яке з'явиться після звернення до зазначеної послуги, в полі Вираз потрібно ввести вираз, значення якого необхідно обчислити, і «натиснути» кнопку Обчислити, після чого результат буде виведено у полі Результат обчислень. При цьому якщо вираз було введено некоректно, то з'явиться повідомлення про помилку.
Для введення виразів можна використовувати панель калькулятора з цифровими кнопками і кнопками швидкого введення назв стандартних функцій, що дозволяє вводити вирази за допомогою лише миші, без використання клавіатури. Без використання панелі калькулятора всі необхідні символи можна ввести також і з клавіатури.
Покажемо застосування цієї програми.
Головною функціональною можливістю програми, яка заявлена розробниками, є перевірка вірності розв’язання геометричних задач. Користувач (учень) має змогу після вирішення поставленої задачі перевірити результат, використавши програму Gran 3D.
Розглянемо можливості програмного продукту на прикладі задач, поданих в шкільному підручнику. Спочатку проводиться вирішення задачі стандартним способом – за допомогою формул та математичних обчислень, після чого знайдені результати перевіряються на правильність.
Задача 1.
Діаметр кулі дорівнює 10 см. Знайти відношення площі поверхні цієї кулі до її об’єму.
Розв'язання стандартним способом:
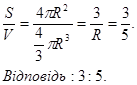
Перевірка:
Викликаємо команду «Створити базовий просторовий об'єкт». У вікні, що появилось, вибираємо вкладку «Куля» (рис. 29).
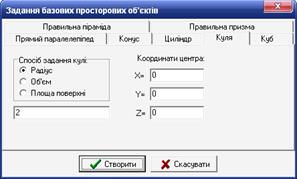
Рис. 29
Вводимо діаметр кулі і натискаємо на кнопку «Створити». Програма будує тримірне зображення кулі, що дозволяє користувачу наглядно оцінити параметри кулі, аналіз якої він проводить (рис. 30).
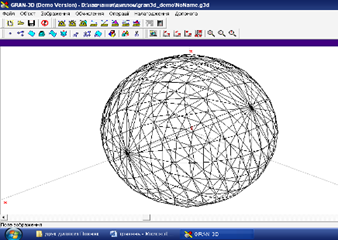
Рис. 30
У вкладеному вікні, що знаходиться з правої сторони, зчитуємо інформацію про об’єкт та площу поверхні (рис. 31).
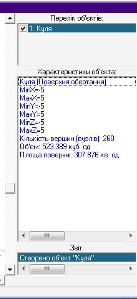
Рис. 31
Обєм: 523 куб. од.
Площа поверхні: 307 кв. од.
Діленням об’єму на площу можна отримати відношення 3 до 5, що є правильним розв’язком задачі.
Задача 2.
Кульку виготовили із скла, її радіус 3 см. Знайти з точністю до десятих грама масу цієї кульки, якщо маса 1 см3 дорівнює 3 г.
Стандартний метод розвязку:
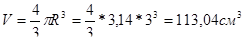
Тоді маса кульки:
3*113,04=339,1 (г)
Перевірка результату. Викликаємо команду побудови базового просторового об’єкту, у вікні вибираємо вкладку «Куля» і вводимо початкові дані (рис. 32).
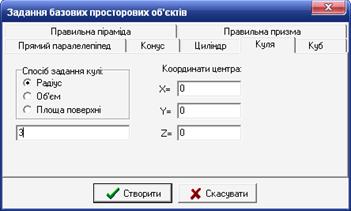
Рис. 32
Створюємо кулю з вказаними параметрами і у вікні з інформацією про об’єкту отримуємо дані про об’єм кулі (рис. 33) і перемножуємо на густину скла. В результаті отримуємо співпадання даних, добутих двома способами.

Рис. 33
Задача 3. Прямокутний трикутник, катети якого дорівнюють 36 см. І 10,5 см, обертається навколо одного катета. Визначити повну поверхню і об’єм утвореного при цьому конуса.
Розв'язання:
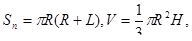
Де R – радіус основи, L – твірна, H – висота.
Розглянемо  , у ньому
, у ньому  .
.
Якщо ОА=10,5см, SO=36см, то за теоремою Піфагора SA2=SO2+OA2=1296+110,25=1406,25, SO=37,5см.
Отже, 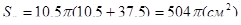
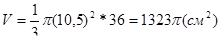
Якщо ОА=36см, SO=10,5, то за теоремою Піфагора
SA2=SO2+OA2=1296+110,25=1406,25, SO=37,5см.
Отже, 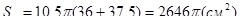
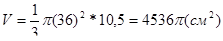
Перевіримо відповідь за допомогою програми Gran 3D. Для цього викличемо команду «Створити просторовий базовий об'єкт», перейдемо на вкладку «Конус» і введемо дані, вказані в умові задачі (рис. 34).
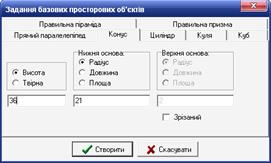
Рис. 34
У вікні параметрів об’єкту читаємо дані про об’єм та повну поверхню утвореного конуса (рис. 35).

Рис. 35
Ділимо отримані дані на Пі і отримуємо результат, відповідний до результату, отриманого стандартним способом розв’язування.
При цьому, разом з перевіркою даних на основі програма будує стереометричну модель об’єкта, що дає можливість побачити його візуально, виконати операції масштабування та обертання для його кращого аналізу (рис. 36).
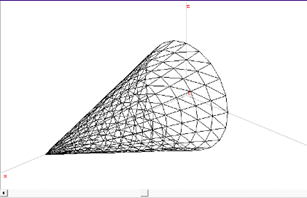
Рис. 36
Отже, програма дозволяє будувати різноманітні просторові об’єкти за допомогою можливостей програми Gran 3D та отримувати дані, необхідні для перевірки даних. Це дає користувачу змогу перевіряти вірність отриманих в процесі розв’язання даних та ефективно аналізувати візуальний вигляд об’єкту.
Висновки
Математична освіта є важливою складовою загальноосвітньої підготовки. Місце математики в системі шкільної освіти визначається її роллю в інтелектуальному, соціальному та моральному розвитку особистості, розумінні будови і використання сучасної науки і техніки, нових інформаційних технологій, сприйманні наукових і технічних ідей, формуванні наукової картини світу і сучасного світогляду. Математика є опорним предметом при вивченні суміжних дисциплін (фізики, хімії, інформатики, біології, географії, економіки, креслення), тому без належної математичної підготовки неможлива повноцінна освіта сучасної людини.
Вирішальне значення для системи шкільної освіти має формуючий вплив предмета математики на розвиток логічного мислення, просторових уявлень і уяви, алгоритмічної і інформаційної культури, уваги, пам’яті.
Просторове мислення, як відомо, є складовою частиною чуттєво-образного мислення і не є апріорі визначеним, запрограмованим від народження. Воно формується в процесі індивідуального розвитку людини. Просторове мислення виникає в надрах практичної потреби орієнтації на місцевості, серед об'єктів матеріального світу. Однією з основних цілей вивчення стереометрії є усвідомлення учнями структури логічної побудови цього розділу. Обов’язковим завданням є розвиток логічного мислення просторової уяви, абстрактного мислення школярів, а також ілюстрація зв’язку геометрії з реальним життям.
Потреба у вивченні елементів стереометрії в курсі математики основної школи, запропонований нами зміст навчального матеріалу, вікові особливості та індивідуальні відмінності дітей підліткового віку у формуванні мислення (зокрема просторового) дають підставу сформулювати такі методичні вимоги до вивчення стереометричного матеріалу в основній школі.
1. Стереометричний матеріал має вивчатися на наочно-оперативному рівні в контексті з відповідним матеріалом курсу математики 5–6-х класів і планіметрії 7–9-х класів. Це дасть змогу одночасно з формуванням знань, навичок і вмінь про плоскі фігури ознайомлювати учнів з геометричними тілами та певними їх властивостями, формувати просторові уявлення, розвивати просторову уяву.
2. Вивчення елементів стереометрії має здійснюватися систематично, з дотриманням принципів навчання.
3. Метою та засобом навчання учнів елементам стереометрії мають бути різнопланові задачі: на розпізнавання геометричних фігур і їх виготовлення; на зображення, вимірювання та обчислення величин. Значна їх кількість має мати прикладну спрямованість. У ході розв'язування задач в учнів мають формуватися просторові уявлення та уява, практичні навички та вміння.
4. Вивчення елементів стереометрії, як і вивчення інших питань шкільного курсу математики, має проводитися диференційовано. Основними критеріями диференціації мають бути рівень вимог до засвоєння учнями навчального матеріалу та рівень допомоги їх з боку вчителя з урахуванням індивідуальних відмінностей.
5. Основною метою вивчення розділу «Елементи стереометрії» в курсі планіметрії 9-го класу має бути систематизація відомостей зі стереометрії, які учні здобули раніше, формування відповідного обсягу стереометричних знань, необхідних для продовження освіти, надання курсу геометрії основної школи певної завершеності.
Для покращення вивчення задач на побудову можна використовувати програмний засіб Gran-3d, який доступний для вивчення вчителями та учнями. Причому його можна знайти в Інтернеті безкоштовно і з його допомогою можна демонструвати розв’язування задач на побудову у русі, динаміці, що значно сприятиме розвитку просторового мислення школярів. Що в кінцевому випадку і є основним завданням вивчення шкільного курсу геометрії.
Дата: 2019-05-29, просмотров: 353.