Усі психічні процеси, зокрема просторова уява, формуються і удосконалюються в результаті діяльності. Таку діяльність необхідно стимулювати й координувати в процесі навчання математики через розв'язування задач. Запропонована нами система вправ має за мету формувати в учнів просторові уявлення, готувати їх до сприйняття стереометричного матеріалу в 10–11-х класах.
Вона включає вправи трьох типів на формування:
1)просторових уявлень та уяви учнів;
2)вимірювальних та обчислювальних навичок;
3)конструктивних навичок.
Належну увагу необхідно приділити формуванню навичок оперування просторовими уявленнями, одержаними в результаті попередньої діяльності. При цьому як засіб наочності разом з моделями геометричних тіл доцільно використовувати їх зображення. Уміння бачити просторові образи на готовому кресленні є важливим стимулом для розвитку просторових уявлень та уяви. У результаті виконання відповідних вправ образи поступово втрачають індивідуальні ознаки, набувають абстрактнішого характеру.
Мінімальний обсяг матеріалу, що вивчається зі стереометрії в основній школі, визначають обов'язкові результати навчання. Наступному накопиченню та переробці у свідомості учнів геометричних фактів, формуванню та розвитку просторових уявлень, конструктивних здібностей має сприяти подана нижче система задач. Для деяких випадків, де це потрібно, описано методику роботи з ними. Задачі підвищеної складності позначено зірочкою (*).
Учні вже мають уявлення про паралельні та перпендикулярні прямі. На другому етапі ми пропонуємо їх перенести і на простір. У зв'язку з цим доцільним є виконання серії вправ на засвоєння учнями взаємного розміщення прямих і площин у просторі. Спочатку це потрібно робити на різних моделях геометричних тіл, поступово переходячи до їх наочних зображень.
Для формування уявлень про взаємне розміщення прямих у просторі, а також прямої та площини, для більшої наочності доцільно використовувати каркасні та скляні моделі. Розглядаючи поняття про взаємне розміщення площин краще користуватися скляними моделями та моделями, виготовленими з картону.
1.На моделі прямої трикутної призми покажіть ребра, які лежать на мимобіжних прямих.
2.На моделі прямокутного паралелепіпеда покажіть ребра, перпендикулярні до нижньої основи.
3.На моделі піраміди покажіть кілька граней, що перетинаються.
4.На моделі циліндра покажіть паралельні грані.
5.Дано модель прямої призми, основою якої є паралелограм. Покажіть:
а) пари паралельних граней;
б) пари перпендикулярних граней.
6. На рис. 18 зображено чотирикутну піраміду SABCD. Назвіть усі ребра, які лежать на прямих, що не перетинають: а) ребро SC; б) ребро AB.
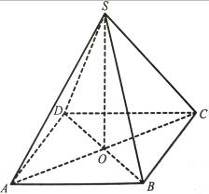
Рис. 18
7. На рис. 19 зображено пряму трикутну призму ABCA1B1C1. Назвіть:
а) ребра, паралельні ребру AA1;
б) ребра, перпендикулярні до ребра BC.
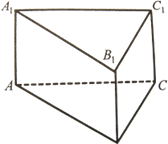
Рис. 19
8. На зображенні прямокутного паралелепіпеда (рис. 20) назвіть:
а) взаємно перпендикулярні грані;
б) грань, паралельну грані BB1C1C.
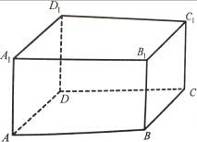
Рис. 20
9. Зобразіть будь-які два відрізки куба (які не є його ребрами) з кінцями у вершинах куба (рис. 21) такі, щоб вони були:
а) паралельними;
б) перпендикулярними;
в) мимобіжними.
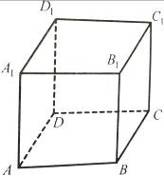
Рис. 21
У 9 класі продовжується формування в учнів уявлень про геометричні тіла за їх розгортками та зображеннями, зокрема під час обчислення площ поверхонь цих тіл за розмірами, поданими на розгортках та зображеннях.
Наведемо приклади таких задач.
10.Розгорткою бічної поверхні циліндра є прямокутник зі сторонами 63 см і 3,2 см. Обчисліть радіус основи циліндра (розгляньте два випадки).
11.Обчисліть площу повної поверхні конуса, якщо твірна конуса дорівнює 12см, центральний кут розгортки 120°.
12. За поданими на розгортках призм розмірами (рис. 22) обчисліть площі їх поверхонь. Основи призм – правильні многокутники. (Одиниці вимірювання подано в дециметрах.)
13.Обчисліть площі поверхонь (бічну та повну) прямих призм за розмірами, поданими на рис. 23. Основи призм – правильні многокутники. (Одиниці вимірювання подано в сантиметрах.)
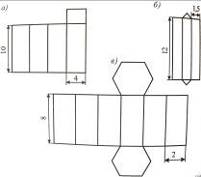
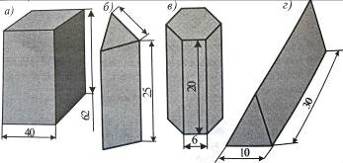
Рис. 22 Рис. 23
Центральне місце на другому етапі відводиться вправам на зображення простіших геометричних тіл. Їх розв'язуванню сприяє попередня підготовча робота, а саме: розпізнавання многогранників і тіл обертання на моделях та їх зображеннях, знаходження плоских фігур на зображеннях геометричних тіл.
Після того як учні ознайомилися з побудовою зображень призми, піраміди, циліндра, конуса, кулі, слід запропонувати їм виконати вправи на закріплення. Зокрема, це можуть бути вправи такого типу.
14. Накресліть прямокутний паралелепіпед і позначте його вершини буквами. Назвіть:
а) ребра, що лежать на паралельних, перпендикулярних, мимобіжних прямих;
б) паралельні, перпендикулярні грані.
15.На зображенні куба проведіть площину так, щоб одержати квадратний переріз куба.
16.На рис. 24 дано зображення куба, на ребрах якого взято три точки. Побудуйте фігуру (переріз), по якій площина, що проходить через дані точки, перетне куб.
17.
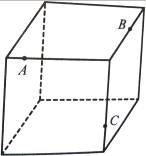
Рис. 24
18.На рис. 25 дано зображення прямокутного паралелепіпеда, на ребрах якого взято три точки. Побудуйте переріз паралелепіпеда площиною, що проходить через дані точки. Яка фігура утворилась у перерізі?
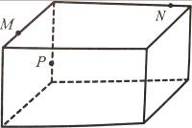
Рис. 25
18.Зобразіть прямий паралелепіпед і проведіть його діагоналі.
19.Зобразіть пряму трикутну призму. Проведіть діагональ бічної грані.
20. Побудуйте зображення прямої трикутної призми. Сполучіть кінці сторони нижньої основи та протилежну вершину верхньої основи. Яка фігура утворилася в перерізі?
21.Зобразіть круговий циліндр. Позначте на зображенні радіус нижньої основи.
22.Зобразіть циліндр та побудуйте зображення його осьового перерізу.
23.Побудуйте зображення циліндра. Позначте точку на колі верхньої основи і точку на колі нижньої основи. Сполучіть їх відрізком.
24. Зобразіть конус. Побудуйте на зображенні діаметр основи.
25.На зображенні конуса побудуйте зображення його осьового перерізу.
26.Побудуйте зображення конуса. Позначте на колі основи конуса точку. Зобразіть твірну конуса, яка містить вибрану точку.
Навички будувати зображення геометричних тіл відпрацьовуються під час подальшого ознайомлення учнів з многогранниками та тілами обертання.
Вивчаючи систематичний курс планіметрії, з метою пропедевтики стереометричних знань велику увагу слід приділити задачам на обчислення лінійних елементів геометричних тіл, які є елементами плоских фігур, за даними розмірами інших елементів і мір кутів цих тіл, а також задачам на встановлення залежності між лінійними елементами та площами плоских фігур, поверхнями та об'ємами геометричних тіл. Учні вчаться знаходити на зображеннях геометричних тіл плоскі фігури та, використовуючи відомості з планіметрії, обчислювати необхідні величини.
Така ілюстрація тверджень планіметрії на геометричних тілах, по-перше, розширює знання учнів про ці тіла, по-друге, значно полегшує засвоєння учнями відповідного планіметричного матеріалу, по-третє, досить сприятливо відбивається на розвитку просторових уявлень учнів, дає змогу здійснювати «вихід» за межі площини. Оскільки формування обчислювальних навичок і вмінь на даному етапі навчання вже не є його основною метою, то там, де це необхідно, рекомендуємо користуватися калькулятором.
Наведемо приклади таких задач.
27.У трикутній піраміді РАВС 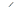 АРС=
АРС= 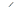 ВРС,
ВРС, 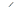 АСР=
АСР= 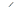 ВСР. Скільки рівнобедрених трикутників серед її граней?
ВСР. Скільки рівнобедрених трикутників серед її граней?
28.У трикутній піраміді PАВС  РВА=90°,
РВА=90°,  РВС=90°. Нехай BA=ВС. Доведіть, що РА=РС.
РВС=90°. Нехай BA=ВС. Доведіть, що РА=РС.
29.Основою піраміди PABC є рівнобедрений трикутник АВС (АB=ВС). ЇЇ бічні ребра рівні. Нехай MN – середня лінія основи, паралельна АС. Доведіть рівність трикутників РВМ і РВN.
30.Дано зображення куба. Сполучіть деякі його вершини так, щоб одержати рівносторонній трикутник.
31.Довжина ребра куба дорівнює 10 см (рис. 26). Обчисліть довжину діагоналі куба.
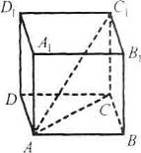
Рис. 26
32. У прямокутному паралелепіпеді ABCDA1BlClDl АВ=5 дм, DD1=2 дм, B1C1=1 дм. Знайдіть B1D.
33. Основою прямої призми ABCDA1BlClDl є паралелограм ABCD зі сторонами 4 см і 8 см, кут BAD дорівнює 60°. Знайдіть діагоналі призми, якщо її висота 6 см.
34.Знайдіть діагональ прямокутного паралелепіпеда, висота якого дорівнює 12, а сторони основи 8 і 6.
35.Знайдіть діагональ прямокутного паралелепіпеда, сторони основи якого дорівнюють 3 дм і 4 дм, якщо вона утворює з діагоналлю основи кут 60°.
36.За даними стороною основи а=9 см і бічним ребром b=6 см знайдіть висоту піраміди, основою якої є квадрат. Основа висоти піраміди збігається з центром квадрата.
37.Основою піраміди є рівносторонній трикутник зі стороною 6 м. Бічні ребра піраміди рівні й утворюють зі сторонами основи кути по 45°. Знайдіть висоту піраміди.
38.Основою піраміди SABCD є прямокутник ABCD. O – точка перетину його діагоналей; SO – висота піраміди. Обчисліть довжину бічного ребра піраміди, якщо довжина діагоналі дорівнює 14 см, а кут між діагоналлю основи та бічним ребром дорівнює 60°.
39.Осьовим перерізом циліндра є прямокутник. Обчисліть площу осьового перерізу, якщо діаметр основи циліндра 22 см, а висота циліндра 40 см.
40.Діагональ осьового перерізу циліндра дорівнює 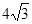 і утворює з площиною основи кут 45°. Знайдіть радіус циліндра.
і утворює з площиною основи кут 45°. Знайдіть радіус циліндра.
41.Знайдіть радіус основи прямого кругового конуса, якщо його твірна 5 м, а висота 4 м.
42.Твірна конуса дорівнює 3 дм, а площа круга основи 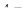 дм2. Знайдіть висоту конуса.
дм2. Знайдіть висоту конуса.
43.Кут при вершині осьового перерізу конуса дорівнює 60°, а твірна дорівнює 2см. Знайдіть площу осьового перерізу.
44.Назвіть і покажіть на каркасній моделі куба його осі симетрії.
45.Скільки осей симетрії має прямокутний паралелепіпед?
46.Що є центром симетрії: а) циліндра; б) кулі?
У 9-му класі пропедевтичне засвоєння знань стереометричних понять завершується розглядом питань на обчислення площ поверхонь та об'ємів многогранників і тіл обертання. У 5–6-х класах учні вже зустрічалися з такими задачами, але під час їх розв'язування вони користувалися готовими формулами.
Після того, як у систематичному курсі планіметрії учні ознайомилися з обчисленням площ плоских фігур, розширили відомості про геометричні тіла, вони набувають чіткіших уявлень про обчислення площ поверхонь та об'ємів многогранників і тіл обертання. Ці уявлення слід закріпити під час розв’язування таких задач.
47.Обчисліть (з точністю до одиниць) радіус основи і висоту циліндра, площа основи якого дорівнює 50 см2, а бічна поверхня 25 см:.
48.Бічна поверхня циліндра дорівнює 200 см2. Чи може довжина кола основи дорівнювати 400 см?
49.Обчисліть об'єм прямої призми, основою якої є рівносторонній трикутник зі стороною 7 мм, а бічне ребро дорівнює 10 мм.
50.Обчисліть площу повної поверхні прямої призми, основою якої є квадрат зі стороною 3 см, а висота призми 7 см.
51.Скільки квадратних метрів заліза потрібно для виготовлення бака з кришкою, що має форму прямої призми, основою якої є правильний шестикутник зі стороною 0,6 м, а висота призми 1,2 м? Витрати на шви становлять 5% від площі поверхні бака.
52.Залізничний насип довжиною 500 м має поперечний переріз у вигляді рівнобічної трапеції з основами 12 м і 8 м, висотою 2,5 м. Скільки тонн землі потрібно для цього насипу? Густина землі 1,3 т/м3.
53.Подвір’я, що має форму прямокутника зі сторонами 32 м і 80 м, треба обгородити. Висота огорожі 2,5 м. Скільки потрібно для цього кубічних метрів дошок товщиною 2,5 см?
54.Обчисліть площу повної поверхні піраміди, основою якої є квадрат зі стороною 12 см, а бічні грані – рівні рівнобедрені трикутники з бічною стороною 20 см.
55.Довжина діагоналі однієї з граней куба дорівнює 6,4 см. Обчисліть об’єм і площу поверхні цього куба.
56.Обчисліть площу повної поверхні та об’єм циліндра, якщо діаметр його основи дорівнює 12 см, а висота 62 см.
57.Знайдіть масу десятиметрової труби, виготовленої зі стального листа товщиною 22 мм, якщо його зовнішній діаметр дорівнює 1420 мм. Густина сталі дорівнює 7800 кг/м3.
58.Посудину, що має форму прямої трикутної призми зі сторонами основи 20см, необхідно замінити рівновеликою посудиною циліндричної форми тієї самої висоти. Знайдіть діаметр основи циліндричної посуди.
59.Що має більшу масу: один вал діаметром 30 см чи два вали, кожний діаметром 15см, якщо всі мають однакову довжину і виготовлені з одного матеріалу?
60.Скільки води містить циліндричний паровий котел, що має довжину 4 м і внутрішній діаметр 1,4 м? Усередині котла по довжині проходять дві жарові труби діаметром по 40 см кожна.
61.Обчисліть площі бічної та повної поверхонь конуса, висота якого дорівнює 6 см, радіус основи 4 см.
62.Скільки тонн породи в териконі висотою 90 м, якщо кут укосу породи 46°, а її густина 2 т/м3 (рис. 27).
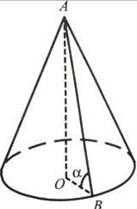
Рис. 27
63.Відсортоване зерно жита зібрали в конічну купу, висота якої 0,7 м. Скільки важить така купа зерна, якщо твірна конічної купи утворює з горизонтальною площиною кут 30°? (Маса 1 дм3 жита 0,7 кг.)
64.Довжина кола основи купи щебеню, що має форму конуса, 12,1 м. Довжина твірної 2,3 м. Обчисліть об'єм цієї купи.
65.Площа поверхні кулі 215 см2. Обчисліть її діаметр.
66.Знайдіть площу поверхні кулі, в якої довжина кола великого круга дорівнює 25 см.
67.Скільки потрібно фарби, щоб пофарбувати кулю діаметром 2,4 м, якщо на пофарбування 1 м2 витрачається 120 г фарби?
68.Знайдіть масу гранітної кулі діаметром 1,8 м. Густина граніту 2,1 кг/дм3.
69.Чому дорівнює маса дубової кулі діаметром 100 мм, якщо густину дуба 0,70 г/см3?
70.Дві металеві кулі діаметром 14 см і 8 см сплавили в одну кулю. Чому дорівнює її діаметр?
Виконання під керівництвом учителя геометричного аналізу запропонованих ситуацій, спостереження предметів навколишньої дійсності, моделей геометричних тіл, їх виготовлення, вправи з використанням зображень, на обчислення елементів тіл, площ поверхонь та об'ємів сприяють накопиченню та переробці в свідомості учнів геометричних фактів, формуванню і розвитку в них конструктивних навичок, просторових уявлень, що забезпечить необхідну базу для вивчення систематичного курсу стереометрії.
Дата: 2019-05-29, просмотров: 320.