Вступ
Дитина дуже рано починає орієнтуватися в оточуючому її реальному, а потім і уявному просторі з урахуванням положення власного тіла. В дослідженнях А.Я. Колодної, Б.Г. Ананьєва, А.А. Люблінської, А.Н. Сорокіна і багато інших показано, що перші просторові образи у дітей виникають при усвідомленні ними схеми свого тіла, залежно від розпізнавання правої і лівої руки (ноги). Всі предмети в просторі вони сприймають з урахуванням його вертикального положення (вгорі – внизу, спереду – ззаду, збоку, справа – зліва і т. д.). Ця природна позиція служить для створення різноманітних і адекватних просторових образів. Орієнтація по схемі тіла є ведучою не тільки при практичному оволодінні простором, але і при переході від реального (фізичного) до уявного (геометричного) простору.
Про це красномовно свідчать дитячі малюнки. Починаючи малювати, діти намагаються перш за все відтворити в малюнку себе або інших «чоловічків». Відтворюючи умовними засобами себе в малюнку, вони стараються на цій основі зробити композиційну побудову малюнка, тобто здійснити просторове розміщення всіх об'єктів. В молодших класах на уроках малювання учні малюють спочатку фігури на площині, але деякі з них вже стараються надавати їм об’ємного вигляду. Пізніше ці фігури зображають в просторі, не знаючи при цьому, що таке трьохвимірний простір. Діти ліплять об’ємні фігури з пластиліну та роблять їх з інших підручних матеріалів. У старших класах вивчення просторових фігур відбувається на уроках стереометрії.
Просторове мислення виникає в надрах практичної потреби орієнтації на місцевості, серед об'єктів матеріального світу. Особливість просторових зв'язків, як підкреслював Ананьєв, полягає в тому, що це є один з видів віддзеркалення відношень між об'єктами. Це означає, що просторові властивості не дані у всьому своєму різноманітті в окремих статичних, ізольованих предметах, застиглих геометричних формах. Вони можуть бути виявлені, вивчені, використані лише в ході активної перетворюючої діяльності суб'єкта, направленої на трансформацію, видозміну об'єктів, в ході якої тільки і можуть бути виділені (знайдені) просторові властивості і відношення.
Розвиток просторового мисленнями дітей відбувається і в процесі навчання. Як відомо, якнайповніше просторові властивості і відношення досліджуються в математиці. З одної сторони, розвиток просторового мислення школярів є необхідним для розвитку у них здібностей до уявлення взагалі, а з другої – це необхідна умова для свідомого засвоєння курсу стереометрії. Формування просторового мислення є одним із найважливіших завдань геометрії. Багато математиків працювали над тим, як покращити процес вивчення геометрії, щоб максимально розвинути просторове мислення учнів.
В даний час ведеться серйозна робота по удосконаленню змісту освіти і шляхів навчання з метою максимального їх наближення до сучасного рівня наукових знань і методів дослідження. В зв'язку з цим розробляються психолого-дидактичні принципи відбору навчального матеріалу з урахуванням досягнень науки і техніки, визначаються оптимальні способи його засвоєння.
На етапі розбудови системи національної освіти та інтеграції її в світову важливим є питання відповідності змісту базової математичної освіти вимогам суспільства, розвитку науки, сучасним потребам особи.
Основна школа в Україні згідно з Законом України «Про освіту» повинна забезпечити базову загальну середню освіту, тобто дати випускникам чітко окреслене коло знань, практичних навичок та умінь, потрібних для роботи в умовах сучасного виробництва, а також для здобуття повної загальної середньої освіти в старшій школі та продовження неперервної освіти.
Специфіка і структура шкільного курсу математики відкривають широкі можливості для розвитку творчих здібностей учнів, формування прийомів розумової діяльності, інтелекту.
У вирішенні цих питань важливе місце належить геометрії, оскільки геометричні знання і вміння є одним із вагомих факторів, що забезпечують, насамперед, готовність людини до неперервної освіти та трудової діяльності.
Оскільки повна загальна середня освіта в Україні є обов'язковою і її можна здобувати у різних типах навчальних закладів освіти, то частина учнів після 9 класу продовжує навчання в загальноосвітній школі, інші вступають до різних училищ, технікумів, ПТУ. Для більшості з тих, хто не продовжує далі навчання в середній школі, стереометрія викладається в меншому обсязі, тому залишаються майже незнайомими властивості просторових фігур, хоча саме вони є необхідними людині в повсякденному житті. Учні професійних навчально-виховних закладів зазнавали труднощів при вивченні спеціальних дисциплін та під час виробничої практики, тому що згідно з діючою раніше програмою в 7–9 класах вони вивчали геометрію на площині, тоді як стереометричні знання та уміння формувалися лише в старшій школі.
Виходячи з цього, виникає необхідність деякого перерозподілу геометричного матеріалу порівняно з діючими програмами. Це стосується, насамперед, вивчення в курсі геометрії основної школи на наочно-інтуїтивному рівні таких понять стереометрії, як паралельність і перпендикулярність прямих і площин, прямокутний паралелепіпед, пряма призма, піраміда, циліндр, конус, куля. Поряд з цим мають формуватися практичні вміння обчислювати площі поверхонь і об'єми основних геометричних тіл, зображати просторові фігури на площині, будувати їх розгортки, «читати» рисунки.
Саме тому у 2003 році, з метою систематизації деяких знань зі стереометрії у школярів основної школи та підготовки їх до вивчення цього курсу у старших класах, у програму з математики для дев’ятого класу введено розділ «Початкові відомості зі стереометрії».
На даний час практично немає розроблених методичних матеріалів, систем задач, які б відповідали нововведенню. Виникла потреба в створенні методики вивчення елементів стереометрії у дев’ятому класі. Тому тема «Про вивчення елементів стереометрії у курсі геометрії дев’ятого класу» є на сьогодні актуальною.
Розкриття цієї теми потребує розв’язання таких задач:
1. Вивчити програму з математики для дев’ятого класу, а особливо розділ «Початкові відомості зі стереометрії»; упорядкувати робочу програму вивчення цього матеріалу в дев’ятому класі.
2. Скласти систему задач до цього розділу.
3. Розробити методичні рекомендації до вивчення елементів стереометрії у дев’ятому класі.
4. Показати дидактичні можливості використання ППЗ GRAN-3D при вивченні елементів стереометрії у 9 класі.
Робота складається з вступу, двох розділів, висновків, списку літературних джерел і додатків.
У першому розділі увага зосереджена на меті і завданні введенню елементів стереометрії у курсі математики основної школи. Також він присвячений для з'ясування, яка роль і місце елементів стереометрії у розвитку просторового мислення школярів.
У другому розділі розглядаються методичні рекомендації вивчення елементів стереометрії у курсі геометрії 9 класу з врахуванням особливостей нових шкільних підручників з геометрії.
Й класи
Довжина відрізка.
1. Накресліть пряму і позначте на ній точки A та B. Виміряйте відрізок АВ. Запишіть, чому дорівнює його довжина.
2. Накресліть відрізки AB та BC, якщо AB=5 см, BC=4 см 3 мм.
3. Виберіть серед запропонованих моделей модель куба. Виміряйте та запишіть довжину його ребра в сантиметрах (з точністю до десятих).
4. Виміряйте та запишіть довжини ребер сірникової коробки в сантиметрах (з точністю до десятих).
Міра кута.
1. Виміряйте кути, зображені на рис. 3; запишіть результати вимірювань.
2. Накресліть кут, градусна міра якого: а) 65°; б) 115°.
3. Які з кутів гострі, а які тупі, якщо 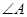 = 67°,
= 67°,  =175°,
=175°, 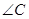 =92°,
=92°, 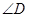 =3°?
=3°?
Трикутник і його елементи.
1. Накресліть трикутник. Назвіть вершини, сторони, кути трикутника.
2. Назвіть трикутники, зображені на рис. 6.

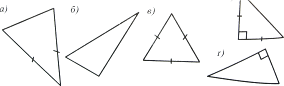
Рис. 6 Рис. 7
3. Назвіть кілька предметів, що вас оточують, які мають форму трикутника.
4. Накресліть прямокутний, гострокутний, тупокутний трикутники.
5. Накресліть рівносторонній, рівнобедрений, рівносторонній трикутники.
6. Серед трикутників, зображених на рис. 7, назвіть:
а) гострокутні, прямокутні, тупокутні;
б) різносторонні, рівнобедрені, рівносторонні.
7. Накресліть гострокутний, прямокутний і тупокутний трикутники та проведіть усі їх висоти.
8. Накресліть довільний трикутник і виміряйте його кути. Знайдіть суму цих кутів.
Піраміда та її елементи.
1. Серед даних моделей пірамід знайдіть:
а) трикутні піраміди; б) чотирикутні піраміди.
2. Які геометричні фігури є бічними гранями піраміди?
3. Скільки бічних граней має трикутна, чотирикутна, п'ятикутна піраміди?
5. Дано модель піраміди. Покажіть:
а) основу піраміди;
б) бічні грані піраміди;
в) вершину піраміди.
6. Яку фігуру зображено на рис. 12? Назвіть:
а) основу зображеної фігури;
б) вершину зображеної фігури;
в) бічні грані цієї фігури;
г) її бічні ребра.
Й класи
Елементи стереометрії
1. Прямі на площині та в просторі. Паралельність і перпендикулярність прямих на площині та в просторі.
1. На моделі прямокутного паралелепіпеда (або на його зображенні) покажіть по дві пари:
а) паралельних прямих; б) перпендикулярних прямих; в) мимобіжних прямих.
2. На каркасній моделі піраміди покажіть прямі, шо не перетинаються.
3. На моделі трикутної піраміди покажіть:
а) дві мимобіжні прямі; б) дві прямі, що перетинаються.
4. На зображенні прямої призми покажіть:
а) дві паралельні прямі; б) дві перпендикулярні прямі; в) дві мимобіжні прямі.
5. На зображенні чотирикутної піраміди покажіть дві мимобіжні прямі.
6. На зображенні куба покажіть дві прямі, паралельні третій.
Рівність трикутників.
1.На зображенні трикутної призми назвіть і покажіть рівні трикутники.
2.Основою піраміди PABCD є прямокутник ABCD. ЇЇ бічні ребра РА, РВ, PC, PD рівні. Для кожної її трикутної грані назвіть рівну їй грань.
3.У чотирикутній піраміді SABCD всі ребра рівні. Встановіть вид трикутників SAB, SAC, BSD.
4.У призмі ABCA1B1C1 бічні грані ABB1A1 та ВСС1В1 рівні. Доведіть, що в трикутнику ABC, який є основою призми, кути А та С рівні.
Коло.
1. На моделі або зображенні циліндра покажіть коло, його центр, радіус.
2. На зображенні конуса проведіть діаметр та хорду кола основи.
3. На каркасній моделі кулі покажіть її центр, радіус, діаметр.
Чотирикутники.
1. На моделі прямої призми, основою якої є паралелограм, покажіть рівні грані.
2. Основою прямої призми є ромб. Доведіть, що її бічні грані – рівні прямокутники.
3. На моделі прямої призми, основою якої є рівнобічна трапеції, покажіть:
а) рівні бічні грані; б) паралельні прямі; в) перпендикулярні прямі.
4. На зображенні піраміди, основою якої є прямокутник, проведіть діагоналі основи та позначте точку їх перетину.
5. Основою піраміди є прямокутник. Бічні ребра піраміди рівні. Доведіть рівність трикутників, що містять вершину піраміди та діагоналі основи.
Теорема Піфагора.
1. Ребро куба дорівнює a. Знайдіть довжину діагоналі його грані.
2. Ребро куба дорівнює a. Знайдіть довжину його діагоналі.
3. Дано зображення прямокутного паралелепіпеда. Знайдіть довжини діагоналей паралелепіпеда, якщо довжини трьох ребер, що виходять з однієї вершини, дорівнюють 2 дм, 3 дм, 6 дм.
4. Обчисліть діагональ бічної грані прямої призми, основою якої є ромб зі стороною 6 см, а бічне ребро дорівнює 8 см.
5. Обчисліть висоту бічної грані піраміди, основою якої є квадрат зі стороною 10 см. Довжина кожного бічного ребра 13 см.
Розв'язування трикутників.
1. Основа прямого паралелепіпеда – ромб зі стороною 6 см і кутом 60°. Висота паралелепіпеда дорівнює 8 см. За готовим зображенням знайдіть довжину меншої діагоналі паралелепіпеда.
2. За готовим зображенням обчисліть діагоналі прямої призми, основою якої є паралелограм зі сторонами 2 см і 3 см та гострим кутом 45°. Висота призми 4 см.
3. Основою піраміди SABCD є прямокутник ABCD. O – точка перетину його діагоналей; 50 – висота піраміди. Обчисліть довжину бічного ребра піраміди, якщо її висота дорівнює 14 см, а кут між діагоналлю основи та бічним ребром 60°. Скористайтесь готовим рисунком.
4. Висота прямої призми, основою якої є квадрат, дорівнює h, а діагональ призми утворює з діагоналлю основи кут 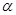 . Знайдіть:
. Знайдіть:
а) діагональ призми; б) діагональ основи призми.
5. Діагональ осьового перерізу циліндра d нахилена до площини його основи під кутом 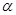 . Знайдіть: а) висоту циліндра; б) діаметр основи.
. Знайдіть: а) висоту циліндра; б) діаметр основи.
17.
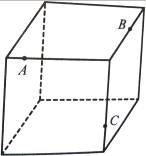
Рис. 24
18.На рис. 25 дано зображення прямокутного паралелепіпеда, на ребрах якого взято три точки. Побудуйте переріз паралелепіпеда площиною, що проходить через дані точки. Яка фігура утворилась у перерізі?
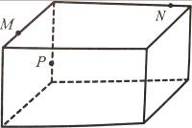
Рис. 25
18.Зобразіть прямий паралелепіпед і проведіть його діагоналі.
19.Зобразіть пряму трикутну призму. Проведіть діагональ бічної грані.
20. Побудуйте зображення прямої трикутної призми. Сполучіть кінці сторони нижньої основи та протилежну вершину верхньої основи. Яка фігура утворилася в перерізі?
21.Зобразіть круговий циліндр. Позначте на зображенні радіус нижньої основи.
22.Зобразіть циліндр та побудуйте зображення його осьового перерізу.
23.Побудуйте зображення циліндра. Позначте точку на колі верхньої основи і точку на колі нижньої основи. Сполучіть їх відрізком.
24. Зобразіть конус. Побудуйте на зображенні діаметр основи.
25.На зображенні конуса побудуйте зображення його осьового перерізу.
26.Побудуйте зображення конуса. Позначте на колі основи конуса точку. Зобразіть твірну конуса, яка містить вибрану точку.
Навички будувати зображення геометричних тіл відпрацьовуються під час подальшого ознайомлення учнів з многогранниками та тілами обертання.
Вивчаючи систематичний курс планіметрії, з метою пропедевтики стереометричних знань велику увагу слід приділити задачам на обчислення лінійних елементів геометричних тіл, які є елементами плоских фігур, за даними розмірами інших елементів і мір кутів цих тіл, а також задачам на встановлення залежності між лінійними елементами та площами плоских фігур, поверхнями та об'ємами геометричних тіл. Учні вчаться знаходити на зображеннях геометричних тіл плоскі фігури та, використовуючи відомості з планіметрії, обчислювати необхідні величини.
Така ілюстрація тверджень планіметрії на геометричних тілах, по-перше, розширює знання учнів про ці тіла, по-друге, значно полегшує засвоєння учнями відповідного планіметричного матеріалу, по-третє, досить сприятливо відбивається на розвитку просторових уявлень учнів, дає змогу здійснювати «вихід» за межі площини. Оскільки формування обчислювальних навичок і вмінь на даному етапі навчання вже не є його основною метою, то там, де це необхідно, рекомендуємо користуватися калькулятором.
Наведемо приклади таких задач.
27.У трикутній піраміді РАВС 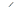 АРС=
АРС= 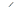 ВРС,
ВРС, 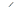 АСР=
АСР= 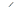 ВСР. Скільки рівнобедрених трикутників серед її граней?
ВСР. Скільки рівнобедрених трикутників серед її граней?
28.У трикутній піраміді PАВС  РВА=90°,
РВА=90°,  РВС=90°. Нехай BA=ВС. Доведіть, що РА=РС.
РВС=90°. Нехай BA=ВС. Доведіть, що РА=РС.
29.Основою піраміди PABC є рівнобедрений трикутник АВС (АB=ВС). ЇЇ бічні ребра рівні. Нехай MN – середня лінія основи, паралельна АС. Доведіть рівність трикутників РВМ і РВN.
30.Дано зображення куба. Сполучіть деякі його вершини так, щоб одержати рівносторонній трикутник.
31.Довжина ребра куба дорівнює 10 см (рис. 26). Обчисліть довжину діагоналі куба.
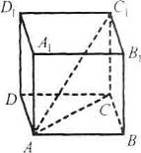
Рис. 26
32. У прямокутному паралелепіпеді ABCDA1BlClDl АВ=5 дм, DD1=2 дм, B1C1=1 дм. Знайдіть B1D.
33. Основою прямої призми ABCDA1BlClDl є паралелограм ABCD зі сторонами 4 см і 8 см, кут BAD дорівнює 60°. Знайдіть діагоналі призми, якщо її висота 6 см.
34.Знайдіть діагональ прямокутного паралелепіпеда, висота якого дорівнює 12, а сторони основи 8 і 6.
35.Знайдіть діагональ прямокутного паралелепіпеда, сторони основи якого дорівнюють 3 дм і 4 дм, якщо вона утворює з діагоналлю основи кут 60°.
36.За даними стороною основи а=9 см і бічним ребром b=6 см знайдіть висоту піраміди, основою якої є квадрат. Основа висоти піраміди збігається з центром квадрата.
37.Основою піраміди є рівносторонній трикутник зі стороною 6 м. Бічні ребра піраміди рівні й утворюють зі сторонами основи кути по 45°. Знайдіть висоту піраміди.
38.Основою піраміди SABCD є прямокутник ABCD. O – точка перетину його діагоналей; SO – висота піраміди. Обчисліть довжину бічного ребра піраміди, якщо довжина діагоналі дорівнює 14 см, а кут між діагоналлю основи та бічним ребром дорівнює 60°.
39.Осьовим перерізом циліндра є прямокутник. Обчисліть площу осьового перерізу, якщо діаметр основи циліндра 22 см, а висота циліндра 40 см.
40.Діагональ осьового перерізу циліндра дорівнює 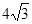 і утворює з площиною основи кут 45°. Знайдіть радіус циліндра.
і утворює з площиною основи кут 45°. Знайдіть радіус циліндра.
41.Знайдіть радіус основи прямого кругового конуса, якщо його твірна 5 м, а висота 4 м.
42.Твірна конуса дорівнює 3 дм, а площа круга основи 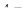 дм2. Знайдіть висоту конуса.
дм2. Знайдіть висоту конуса.
43.Кут при вершині осьового перерізу конуса дорівнює 60°, а твірна дорівнює 2см. Знайдіть площу осьового перерізу.
44.Назвіть і покажіть на каркасній моделі куба його осі симетрії.
45.Скільки осей симетрії має прямокутний паралелепіпед?
46.Що є центром симетрії: а) циліндра; б) кулі?
У 9-му класі пропедевтичне засвоєння знань стереометричних понять завершується розглядом питань на обчислення площ поверхонь та об'ємів многогранників і тіл обертання. У 5–6-х класах учні вже зустрічалися з такими задачами, але під час їх розв'язування вони користувалися готовими формулами.
Після того, як у систематичному курсі планіметрії учні ознайомилися з обчисленням площ плоских фігур, розширили відомості про геометричні тіла, вони набувають чіткіших уявлень про обчислення площ поверхонь та об'ємів многогранників і тіл обертання. Ці уявлення слід закріпити під час розв’язування таких задач.
47.Обчисліть (з точністю до одиниць) радіус основи і висоту циліндра, площа основи якого дорівнює 50 см2, а бічна поверхня 25 см:.
48.Бічна поверхня циліндра дорівнює 200 см2. Чи може довжина кола основи дорівнювати 400 см?
49.Обчисліть об'єм прямої призми, основою якої є рівносторонній трикутник зі стороною 7 мм, а бічне ребро дорівнює 10 мм.
50.Обчисліть площу повної поверхні прямої призми, основою якої є квадрат зі стороною 3 см, а висота призми 7 см.
51.Скільки квадратних метрів заліза потрібно для виготовлення бака з кришкою, що має форму прямої призми, основою якої є правильний шестикутник зі стороною 0,6 м, а висота призми 1,2 м? Витрати на шви становлять 5% від площі поверхні бака.
52.Залізничний насип довжиною 500 м має поперечний переріз у вигляді рівнобічної трапеції з основами 12 м і 8 м, висотою 2,5 м. Скільки тонн землі потрібно для цього насипу? Густина землі 1,3 т/м3.
53.Подвір’я, що має форму прямокутника зі сторонами 32 м і 80 м, треба обгородити. Висота огорожі 2,5 м. Скільки потрібно для цього кубічних метрів дошок товщиною 2,5 см?
54.Обчисліть площу повної поверхні піраміди, основою якої є квадрат зі стороною 12 см, а бічні грані – рівні рівнобедрені трикутники з бічною стороною 20 см.
55.Довжина діагоналі однієї з граней куба дорівнює 6,4 см. Обчисліть об’єм і площу поверхні цього куба.
56.Обчисліть площу повної поверхні та об’єм циліндра, якщо діаметр його основи дорівнює 12 см, а висота 62 см.
57.Знайдіть масу десятиметрової труби, виготовленої зі стального листа товщиною 22 мм, якщо його зовнішній діаметр дорівнює 1420 мм. Густина сталі дорівнює 7800 кг/м3.
58.Посудину, що має форму прямої трикутної призми зі сторонами основи 20см, необхідно замінити рівновеликою посудиною циліндричної форми тієї самої висоти. Знайдіть діаметр основи циліндричної посуди.
59.Що має більшу масу: один вал діаметром 30 см чи два вали, кожний діаметром 15см, якщо всі мають однакову довжину і виготовлені з одного матеріалу?
60.Скільки води містить циліндричний паровий котел, що має довжину 4 м і внутрішній діаметр 1,4 м? Усередині котла по довжині проходять дві жарові труби діаметром по 40 см кожна.
61.Обчисліть площі бічної та повної поверхонь конуса, висота якого дорівнює 6 см, радіус основи 4 см.
62.Скільки тонн породи в териконі висотою 90 м, якщо кут укосу породи 46°, а її густина 2 т/м3 (рис. 27).
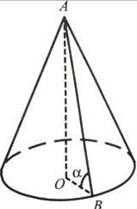
Рис. 27
63.Відсортоване зерно жита зібрали в конічну купу, висота якої 0,7 м. Скільки важить така купа зерна, якщо твірна конічної купи утворює з горизонтальною площиною кут 30°? (Маса 1 дм3 жита 0,7 кг.)
64.Довжина кола основи купи щебеню, що має форму конуса, 12,1 м. Довжина твірної 2,3 м. Обчисліть об'єм цієї купи.
65.Площа поверхні кулі 215 см2. Обчисліть її діаметр.
66.Знайдіть площу поверхні кулі, в якої довжина кола великого круга дорівнює 25 см.
67.Скільки потрібно фарби, щоб пофарбувати кулю діаметром 2,4 м, якщо на пофарбування 1 м2 витрачається 120 г фарби?
68.Знайдіть масу гранітної кулі діаметром 1,8 м. Густина граніту 2,1 кг/дм3.
69.Чому дорівнює маса дубової кулі діаметром 100 мм, якщо густину дуба 0,70 г/см3?
70.Дві металеві кулі діаметром 14 см і 8 см сплавили в одну кулю. Чому дорівнює її діаметр?
Виконання під керівництвом учителя геометричного аналізу запропонованих ситуацій, спостереження предметів навколишньої дійсності, моделей геометричних тіл, їх виготовлення, вправи з використанням зображень, на обчислення елементів тіл, площ поверхонь та об'ємів сприяють накопиченню та переробці в свідомості учнів геометричних фактів, формуванню і розвитку в них конструктивних навичок, просторових уявлень, що забезпечить необхідну базу для вивчення систематичного курсу стереометрії.
Активація програми.
Програма GRAN-3D призначена для графічного аналізу просторових (тривимірних) об'єктів, звідки й походить її назва (GRaphic Analysis 3-Dimension).
Програма функціонує під управлінням операційної системи Windows9x. Після успішної установки в зазначеному директорії буде створено файл GRAN3D.EXE – основна програма, а також будуть створені допоміжні файли допомоги. Далі після «натискання» кнопки Пуск назва програми GRAN-3D буде з'являтися як пункт меню Програми, при зверненні до якого буде відбуватися запуск ППС GRAN-3D.
Панель інструментів.
Для активації деяких послуг можна скористатися кнопками швидкого виклику операцій на панелі інструментів, яка розташована під головним меню програми. Для цього треба натиснути відповідну кнопку (тобто встановити покажчик миші на позначення кнопки і натиснути ліву клавішу миші). «Кнопки» оснащені системою оперативної підказки, тому під час знаходження покажчика миші над певною «кнопкою» на екрані з'являються короткі відомості про її призначення.
Поворот системи координат.
За допомогою смуг повороту зображення можна обертати систему координат разом з створеними моделями об'єктів. Центром повороту може бути точка з довільними просторовими координатами (за замовчуванням центром повороту є точка з координатами (0,0,0)). Щоб змінити координати центру повороту, слід скористатися послугою Установки \ Параметри на вкладиші Зображення вікна Налаштування. Для повороту системи навколо осі Oz призначена горизонтальна смуга повороту зображення, а для повороту навколо горизонталі, що проходить через центр повороту, призначена вертикальна смуга повороту зображення. Для повороту системи можна використовувати також клавіші управління курсором.
Означення координат точок
Якщо підвести вказівник мишки до будь-якої лінії довільного об'єкта, зазначена лінія виділяється пунктиром і в полі інформування автоматично виводяться просторові координати точки, яка відповідає сучасному стану покажчика, і назва об'єкта, з яким ця точка належить. У випадку, якщо система розміщена так, що одна з координатних осей вироджується в точку (тобто координатна площина, яка визначається іншими двома осями, розміщена паралельно площині зображення), автоматично обчислюються (і виводяться в поле інформування) координати точки, яка відповідає сучасному стану покажчика миші в площині зображення. Координата вздовж вироджений осі вважається невідомою.
Характеристика об’єктів.
Задача 1.
Діаметр кулі дорівнює 10 см. Знайти відношення площі поверхні цієї кулі до її об’єму.
Розв'язання стандартним способом:
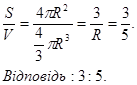
Перевірка:
Викликаємо команду «Створити базовий просторовий об'єкт». У вікні, що появилось, вибираємо вкладку «Куля» (рис. 29).
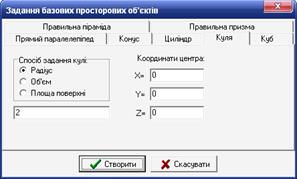
Рис. 29
Вводимо діаметр кулі і натискаємо на кнопку «Створити». Програма будує тримірне зображення кулі, що дозволяє користувачу наглядно оцінити параметри кулі, аналіз якої він проводить (рис. 30).
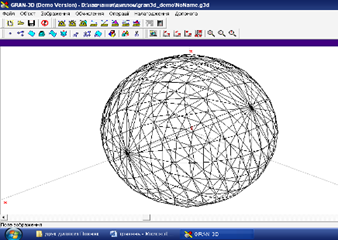
Рис. 30
У вкладеному вікні, що знаходиться з правої сторони, зчитуємо інформацію про об’єкт та площу поверхні (рис. 31).
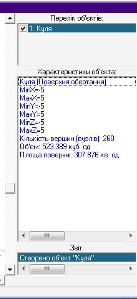
Рис. 31
Обєм: 523 куб. од.
Площа поверхні: 307 кв. од.
Діленням об’єму на площу можна отримати відношення 3 до 5, що є правильним розв’язком задачі.
Задача 2.
Кульку виготовили із скла, її радіус 3 см. Знайти з точністю до десятих грама масу цієї кульки, якщо маса 1 см3 дорівнює 3 г.
Стандартний метод розвязку:
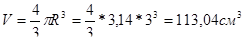
Тоді маса кульки:
3*113,04=339,1 (г)
Перевірка результату. Викликаємо команду побудови базового просторового об’єкту, у вікні вибираємо вкладку «Куля» і вводимо початкові дані (рис. 32).
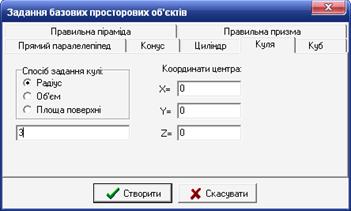
Рис. 32
Створюємо кулю з вказаними параметрами і у вікні з інформацією про об’єкту отримуємо дані про об’єм кулі (рис. 33) і перемножуємо на густину скла. В результаті отримуємо співпадання даних, добутих двома способами.

Рис. 33
Задача 3. Прямокутний трикутник, катети якого дорівнюють 36 см. І 10,5 см, обертається навколо одного катета. Визначити повну поверхню і об’єм утвореного при цьому конуса.
Розв'язання:
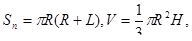
Де R – радіус основи, L – твірна, H – висота.
Розглянемо  , у ньому
, у ньому  .
.
Якщо ОА=10,5см, SO=36см, то за теоремою Піфагора SA2=SO2+OA2=1296+110,25=1406,25, SO=37,5см.
Отже, 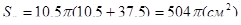
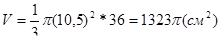
Якщо ОА=36см, SO=10,5, то за теоремою Піфагора
SA2=SO2+OA2=1296+110,25=1406,25, SO=37,5см.
Отже, 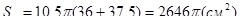
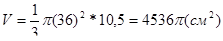
Перевіримо відповідь за допомогою програми Gran 3D. Для цього викличемо команду «Створити просторовий базовий об'єкт», перейдемо на вкладку «Конус» і введемо дані, вказані в умові задачі (рис. 34).
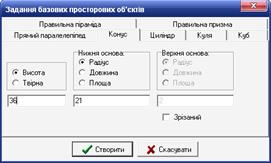
Рис. 34
У вікні параметрів об’єкту читаємо дані про об’єм та повну поверхню утвореного конуса (рис. 35).

Рис. 35
Ділимо отримані дані на Пі і отримуємо результат, відповідний до результату, отриманого стандартним способом розв’язування.
При цьому, разом з перевіркою даних на основі програма будує стереометричну модель об’єкта, що дає можливість побачити його візуально, виконати операції масштабування та обертання для його кращого аналізу (рис. 36).
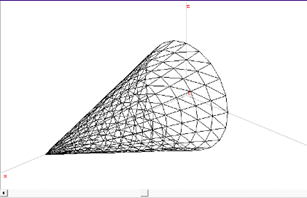
Рис. 36
Отже, програма дозволяє будувати різноманітні просторові об’єкти за допомогою можливостей програми Gran 3D та отримувати дані, необхідні для перевірки даних. Це дає користувачу змогу перевіряти вірність отриманих в процесі розв’язання даних та ефективно аналізувати візуальний вигляд об’єкту.
Висновки
Математична освіта є важливою складовою загальноосвітньої підготовки. Місце математики в системі шкільної освіти визначається її роллю в інтелектуальному, соціальному та моральному розвитку особистості, розумінні будови і використання сучасної науки і техніки, нових інформаційних технологій, сприйманні наукових і технічних ідей, формуванні наукової картини світу і сучасного світогляду. Математика є опорним предметом при вивченні суміжних дисциплін (фізики, хімії, інформатики, біології, географії, економіки, креслення), тому без належної математичної підготовки неможлива повноцінна освіта сучасної людини.
Вирішальне значення для системи шкільної освіти має формуючий вплив предмета математики на розвиток логічного мислення, просторових уявлень і уяви, алгоритмічної і інформаційної культури, уваги, пам’яті.
Просторове мислення, як відомо, є складовою частиною чуттєво-образного мислення і не є апріорі визначеним, запрограмованим від народження. Воно формується в процесі індивідуального розвитку людини. Просторове мислення виникає в надрах практичної потреби орієнтації на місцевості, серед об'єктів матеріального світу. Однією з основних цілей вивчення стереометрії є усвідомлення учнями структури логічної побудови цього розділу. Обов’язковим завданням є розвиток логічного мислення просторової уяви, абстрактного мислення школярів, а також ілюстрація зв’язку геометрії з реальним життям.
Потреба у вивченні елементів стереометрії в курсі математики основної школи, запропонований нами зміст навчального матеріалу, вікові особливості та індивідуальні відмінності дітей підліткового віку у формуванні мислення (зокрема просторового) дають підставу сформулювати такі методичні вимоги до вивчення стереометричного матеріалу в основній школі.
1. Стереометричний матеріал має вивчатися на наочно-оперативному рівні в контексті з відповідним матеріалом курсу математики 5–6-х класів і планіметрії 7–9-х класів. Це дасть змогу одночасно з формуванням знань, навичок і вмінь про плоскі фігури ознайомлювати учнів з геометричними тілами та певними їх властивостями, формувати просторові уявлення, розвивати просторову уяву.
2. Вивчення елементів стереометрії має здійснюватися систематично, з дотриманням принципів навчання.
3. Метою та засобом навчання учнів елементам стереометрії мають бути різнопланові задачі: на розпізнавання геометричних фігур і їх виготовлення; на зображення, вимірювання та обчислення величин. Значна їх кількість має мати прикладну спрямованість. У ході розв'язування задач в учнів мають формуватися просторові уявлення та уява, практичні навички та вміння.
4. Вивчення елементів стереометрії, як і вивчення інших питань шкільного курсу математики, має проводитися диференційовано. Основними критеріями диференціації мають бути рівень вимог до засвоєння учнями навчального матеріалу та рівень допомоги їх з боку вчителя з урахуванням індивідуальних відмінностей.
5. Основною метою вивчення розділу «Елементи стереометрії» в курсі планіметрії 9-го класу має бути систематизація відомостей зі стереометрії, які учні здобули раніше, формування відповідного обсягу стереометричних знань, необхідних для продовження освіти, надання курсу геометрії основної школи певної завершеності.
Для покращення вивчення задач на побудову можна використовувати програмний засіб Gran-3d, який доступний для вивчення вчителями та учнями. Причому його можна знайти в Інтернеті безкоштовно і з його допомогою можна демонструвати розв’язування задач на побудову у русі, динаміці, що значно сприятиме розвитку просторового мислення школярів. Що в кінцевому випадку і є основним завданням вивчення шкільного курсу геометрії.
Вступ
Дитина дуже рано починає орієнтуватися в оточуючому її реальному, а потім і уявному просторі з урахуванням положення власного тіла. В дослідженнях А.Я. Колодної, Б.Г. Ананьєва, А.А. Люблінської, А.Н. Сорокіна і багато інших показано, що перші просторові образи у дітей виникають при усвідомленні ними схеми свого тіла, залежно від розпізнавання правої і лівої руки (ноги). Всі предмети в просторі вони сприймають з урахуванням його вертикального положення (вгорі – внизу, спереду – ззаду, збоку, справа – зліва і т. д.). Ця природна позиція служить для створення різноманітних і адекватних просторових образів. Орієнтація по схемі тіла є ведучою не тільки при практичному оволодінні простором, але і при переході від реального (фізичного) до уявного (геометричного) простору.
Про це красномовно свідчать дитячі малюнки. Починаючи малювати, діти намагаються перш за все відтворити в малюнку себе або інших «чоловічків». Відтворюючи умовними засобами себе в малюнку, вони стараються на цій основі зробити композиційну побудову малюнка, тобто здійснити просторове розміщення всіх об'єктів. В молодших класах на уроках малювання учні малюють спочатку фігури на площині, але деякі з них вже стараються надавати їм об’ємного вигляду. Пізніше ці фігури зображають в просторі, не знаючи при цьому, що таке трьохвимірний простір. Діти ліплять об’ємні фігури з пластиліну та роблять їх з інших підручних матеріалів. У старших класах вивчення просторових фігур відбувається на уроках стереометрії.
Просторове мислення виникає в надрах практичної потреби орієнтації на місцевості, серед об'єктів матеріального світу. Особливість просторових зв'язків, як підкреслював Ананьєв, полягає в тому, що це є один з видів віддзеркалення відношень між об'єктами. Це означає, що просторові властивості не дані у всьому своєму різноманітті в окремих статичних, ізольованих предметах, застиглих геометричних формах. Вони можуть бути виявлені, вивчені, використані лише в ході активної перетворюючої діяльності суб'єкта, направленої на трансформацію, видозміну об'єктів, в ході якої тільки і можуть бути виділені (знайдені) просторові властивості і відношення.
Розвиток просторового мисленнями дітей відбувається і в процесі навчання. Як відомо, якнайповніше просторові властивості і відношення досліджуються в математиці. З одної сторони, розвиток просторового мислення школярів є необхідним для розвитку у них здібностей до уявлення взагалі, а з другої – це необхідна умова для свідомого засвоєння курсу стереометрії. Формування просторового мислення є одним із найважливіших завдань геометрії. Багато математиків працювали над тим, як покращити процес вивчення геометрії, щоб максимально розвинути просторове мислення учнів.
В даний час ведеться серйозна робота по удосконаленню змісту освіти і шляхів навчання з метою максимального їх наближення до сучасного рівня наукових знань і методів дослідження. В зв'язку з цим розробляються психолого-дидактичні принципи відбору навчального матеріалу з урахуванням досягнень науки і техніки, визначаються оптимальні способи його засвоєння.
На етапі розбудови системи національної освіти та інтеграції її в світову важливим є питання відповідності змісту базової математичної освіти вимогам суспільства, розвитку науки, сучасним потребам особи.
Основна школа в Україні згідно з Законом України «Про освіту» повинна забезпечити базову загальну середню освіту, тобто дати випускникам чітко окреслене коло знань, практичних навичок та умінь, потрібних для роботи в умовах сучасного виробництва, а також для здобуття повної загальної середньої освіти в старшій школі та продовження неперервної освіти.
Специфіка і структура шкільного курсу математики відкривають широкі можливості для розвитку творчих здібностей учнів, формування прийомів розумової діяльності, інтелекту.
У вирішенні цих питань важливе місце належить геометрії, оскільки геометричні знання і вміння є одним із вагомих факторів, що забезпечують, насамперед, готовність людини до неперервної освіти та трудової діяльності.
Оскільки повна загальна середня освіта в Україні є обов'язковою і її можна здобувати у різних типах навчальних закладів освіти, то частина учнів після 9 класу продовжує навчання в загальноосвітній школі, інші вступають до різних училищ, технікумів, ПТУ. Для більшості з тих, хто не продовжує далі навчання в середній школі, стереометрія викладається в меншому обсязі, тому залишаються майже незнайомими властивості просторових фігур, хоча саме вони є необхідними людині в повсякденному житті. Учні професійних навчально-виховних закладів зазнавали труднощів при вивченні спеціальних дисциплін та під час виробничої практики, тому що згідно з діючою раніше програмою в 7–9 класах вони вивчали геометрію на площині, тоді як стереометричні знання та уміння формувалися лише в старшій школі.
Виходячи з цього, виникає необхідність деякого перерозподілу геометричного матеріалу порівняно з діючими програмами. Це стосується, насамперед, вивчення в курсі геометрії основної школи на наочно-інтуїтивному рівні таких понять стереометрії, як паралельність і перпендикулярність прямих і площин, прямокутний паралелепіпед, пряма призма, піраміда, циліндр, конус, куля. Поряд з цим мають формуватися практичні вміння обчислювати площі поверхонь і об'єми основних геометричних тіл, зображати просторові фігури на площині, будувати їх розгортки, «читати» рисунки.
Саме тому у 2003 році, з метою систематизації деяких знань зі стереометрії у школярів основної школи та підготовки їх до вивчення цього курсу у старших класах, у програму з математики для дев’ятого класу введено розділ «Початкові відомості зі стереометрії».
На даний час практично немає розроблених методичних матеріалів, систем задач, які б відповідали нововведенню. Виникла потреба в створенні методики вивчення елементів стереометрії у дев’ятому класі. Тому тема «Про вивчення елементів стереометрії у курсі геометрії дев’ятого класу» є на сьогодні актуальною.
Розкриття цієї теми потребує розв’язання таких задач:
1. Вивчити програму з математики для дев’ятого класу, а особливо розділ «Початкові відомості зі стереометрії»; упорядкувати робочу програму вивчення цього матеріалу в дев’ятому класі.
2. Скласти систему задач до цього розділу.
3. Розробити методичні рекомендації до вивчення елементів стереометрії у дев’ятому класі.
4. Показати дидактичні можливості використання ППЗ GRAN-3D при вивченні елементів стереометрії у 9 класі.
Робота складається з вступу, двох розділів, висновків, списку літературних джерел і додатків.
У першому розділі увага зосереджена на меті і завданні введенню елементів стереометрії у курсі математики основної школи. Також він присвячений для з'ясування, яка роль і місце елементів стереометрії у розвитку просторового мислення школярів.
У другому розділі розглядаються методичні рекомендації вивчення елементів стереометрії у курсі геометрії 9 класу з врахуванням особливостей нових шкільних підручників з геометрії.
Елементи стереометрії у шкільному курсі математики
Дата: 2019-05-29, просмотров: 425.