Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

В данном разделе проводится вывод уравнения движения электропривода асинхронного электродвигателя, находящегося в генераторе вдоха. Для более точной работы двигателя, на его выходном валу был установлен тахогенератор, в результате чего получилась следящая система.

Дифференциальное уравнение системы может быть найдено из уравнений ее элементов путем их совместного решения.

Прежде всего запишем уравнения отдельных элементов системы. Для элемента сравнения справедливо соотношение

q = a _вх – a _вых , (1.4.1)

 

где q – рассогласование, снимаемое с элемента сравнения;

a _вх и a _вых – соответственно углы поворота входного и выходного валов системы.

Для преобразователя запишем уравнение

U _q = k_n q , (1.4.2)

 

где U _q – измеритель рассогласования (потенциометры);

k_n – коэффициент пропорциональности, характеризующий крутизну характеристики U _q = f ( q ) преобразователя.

Коэффициент пропорциональности можно выразить как k_n=U_q/q и измерять в вольтах на градус. Таким образом, этот коэффициент показывает, какое напряжение сигнала ошибки приходится на единицу угла рассогласования.

Для тахогенератора

U_m = k_m 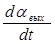; (1.4.3)

 

Для усилителя

U_a = k_yU _вх , (1.4.4)

где U _а – выходное напряжение усилителя, поступающее в цепь якоря исполнительного двигателя;

k_y – коэффициент усиления усилителя по напряжению;

U _вх = U _q – U_m ; (1.4.5)

 

Для того чтобы вывести дифференциальное уравнение двигателя, рассмотрим протекающие в нем процессы, принимая следующие допущения:

- внутреннее сопротивление выходного каскада усилителя равно нулю;

- коэффициент самоиндукции цепи равен нулю;

- Реакция якоря отсутствует.

Уравнение равновесия э.д.с. для цепи якоря двигателя имеет следующий вид:

U_a = I_aR_a + E_a , (1.4.6)

 

где U_a – приложенное к цепи якоря напряжение;

I_a – ток якоря;

R_a – сопротивление якоря;

E_a – противо-э.д.с., возникающая в обмотке якоря при вращении.

На основании закона Фарадея получим

E_a = k_e Ф W , (1.4.7)

 

где k_e – коэффициент пропорциональности, характеризующий конструкцию электродвигателя;

Ф – поток возбуждения;

W – скорость вращения ротора.

Подставив (2.4.7) в (2.4.6), получим

 

U_a = I_aR_a + k_e Ф W , (1.4.8)

 

Запишем уравнение равновесия моментов электродвигателя

М_вр=М_ст+М_дин, (1.49)

 

Электромагнитный вращающий момент двигателя М_вр может быть выражен как

М_вр= k _м Ф I_a , (1.4.10)

 

где k _м – коэффициент пропорциональности, характеризующий магнитную проводимость магнитопровода электродвигателя.

Статический момент М_ст, действующий на валу двигателя, можно представить как

М_ст=М_хх+М_н, (1.4.11)

 

где М_хх – момент холостого хода;

М_н – момент создаваемый нагрузкой.

Динамический момент на валу двигателя М_дин имеет место при изменении скорости вращения и может быть выражен как

М_дин= J 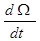, (1.4.12)

 

где J – момент инерции вращающихся частей;

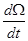 – ускорение вращения.

Решим уравнение (2.4.8) относительно тока якоря I_a:

I_a = 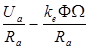, (1.4.13)

 

Подставив (2.4.13) в (2.4.10) получим:

М_вр= 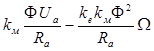, (1.4.14)

 

Полученное уравнение (2.4.14) называется уравнением механической характеристики электродвигателя, которая представляет собой зависимость W = f (М) между моментом на валу двигателя и скоростью его вращения.

Для построения механической характеристики найдем точки ее пересечения с осями координат. Если по оси абсцисс откладывать момент М_вр, а по оси ординат – скорость вращения W, то, учитывая, что уравнение (2.4.14) относительно интересующих нас значений М_вр и W является уравнением первой степени, можно представить механическую характеристику двигателя в виде прямой, пересекающей оси координат в двух точках.

Для нахождения точки пересечения характеристики с осью абсцисс положим

W =0. С учетом этого условия из уравнения (2.4.14) получим

М_вр=М _n = 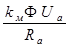, (1.4.15)

 

где М _n – пусковой момент двигателя, т.е. момент вращения, развиваемый двигателем при пуске, когда W =0.

Для определения точки пересечения характеристики с осью ординат положим М_вр=0 и подставив это условие в уравнение (2.4.14), получим

0= 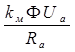-  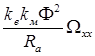(1.4.16)

 

где W _хх – скорость холостого хода двигателя (при отсутствии нагрузки на его валу).

Решим уравнение (2.4.16) относительно скорости. Получим

 

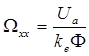. (1.4.17)

 

Построим по полученным точкам механическую характеристику двигателя.

Из приведенного графика, а также уравнений (2.4.14) и (2.4.15) вытекает следующее соотношение:

М_вр=М _n - F W , (1.4.18)

 

где F = 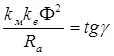 называется коэффициентом вязкого трения двигателя и характеризует жесткость его механической характеристики.

Из выражения (2.4.15) можно получить следующее соотношение

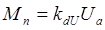, (1.4.19)

где 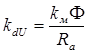 – коэффициент пропорциональности между пусковым моментом двигателя и приложенным к его якорю напряжением.

Из уравнений (2.4.4), (2.4.3) и (2.4.5) выразим входное напряжение усилителя следующим образом:

U _вх ⁼ k_n q - k_{m 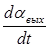,} (1.4.20)

 

тогда выходное напряжение усилителя

U_a = k_nk_y q - k_mk_{y 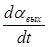,} (1.4.21)

 

при этом пусковой момент двигателя

М _n = k_nk_yk_dU q – k_mk_yk_dU 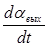, (1.4.22)

 

где К₀= k_nk_yk_dU – передаточный коэффициент системы;

F ₁ = k_mk_yk_dU – коэффициент успокоения, вносимого тахогенератором.

Получим

М _n = K ₀ q – F _{1 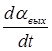.} (1.4.23)

 

Подставив (2.4.24) в (2.4.18), получим

М_вр=К₀ q – F ₁ 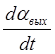  - F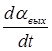

или

М_вр=К₀ q – ( F + F ₁ ) 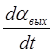. (1.4.24)

 

Уравнение равновесия моментов двигателя запишется в следующем виде:

 

К₀q – (F+F₁) 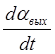= 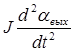+М_ст (1.4.25)

 

Производя замену a_вых=a_вх – q, получим

 

 

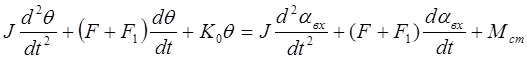
Это выражение представляет собой дифференциальное уравнение движения следящей системы с принимающим тахогенератором.

Важнейшим показателем, характеризующими поведение система, является ошибка слежения q. Получим выражения для статической и динамической установившихся ошибок.

Так как статическая ошибка q_ст оценивается по окончании движения, т.е. при неподвижных входном и выходном валах, примем 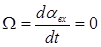. Из этого следует, что 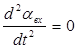. А так как в состоянии покоя системы ее ошибка должна быть постоянна, то  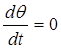и .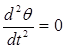

Отсюда получим

К₀ q _ст =М_ст (1.4.26)

 

откуда

q _ст = 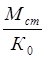. (1.4.27)

 

Полагая, что входной и выходной валы движутся с одинаковой постоянной скоростью W = W _уст = const, примем 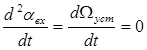. А так как в установившемся режиме ошибка слежения постоянна, то  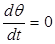и 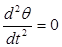. Отсюда получим

К₀ q =( F + F ₁ ) W _уст +М_ст, (1.4.28)

но q = q _ст + q _dy. (1.4.29)

 

Следовательно,

К₀( q _ст + q _dy )=( F + F ₁ ) W _уст +М_ст, (1.4.30)

 

отсюда

q _ст + q _dy = 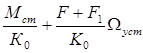 (1.4.31)

 

или, учитывая формулу (2.4.27),

q _dy = 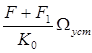 (1.4.32)