Ефективна робота теплопроводів визначається не тільки їх геометрією, але й властивостями матеріалу. В першу чергу мова піде про теплопровідність λ, яка входить у всі наведені раніше розрахункові формули кондуктивної теплопередачі.

Матеріал зі значенням теплопровідності 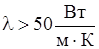 вважається теплопровідним. Тобто такі матеріали в загальному випадку здатні забезпечити відвід тепла від нагрітого елемента, запобігаючи його перегріву. Матеріали зі значенням теплопровідності  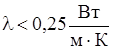вважаються теплоізоляційними. Розглянемо теплопровідності основних видів матеріалів більш детально.

Теплопровідність газів лежить у межах: 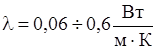 (тільки у гелію і водню ці значення у п’ять разів більші). З ростом абсолютної температури Т їх теплопровідність зростає практично лінійно.

Теплопровідність рідин лежить в межах 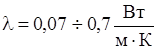. Проте якщо в асоційованих рідинах (вода та ін.) з ростом Т значення λ зростають згідно параболічного закону, то у неасоційованих рідин (бензол та ін.) з ростом Т значення λ падають згідно параболічного закону.

Теплопровідність металів лежить в межах . У чистих металах при зростанні Т значення λ падає згідно параболічного закону, у сплавах – зростає лінійно.

Значення теплопровідності діелектриків лежить в межах . З ростом абсолютної температури Т значення λ зростає майже параболічно.

Особливе місце займають алмази (природні і штучні). Вони мають особливо високу теплопровідність 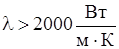. Це визначає їх широке застосування в електронній техніці (напівпровідникові прилади, інтегральні мікросхеми, тощо). Алмази дозволяють зменшити теплові опори між кристалами та корпусом.

Для зменшення теплового навантаження елементів електронних приладів потрібно:

· використовувати матеріали з високим значенням λ;

· збільшувати площу контакту елементів теплопроводів;

· зменшувати шляхи теплопотоків.

Для цього потрібно знімати з контактів лаки, фарби, зменшувати шорсткість поверхонь і збільшувати тиск між ними, в якості прокладок використовувати пасти високої провідності, застосовувати шини між елементами і корпусом, замінювати гумові прокладки на свинцеві, застосовувати самонарізні гвинти.

В якості теплопровідних найбільше застосування знайшли такі матеріали:

· мідь і алюміній для зниження контактного опору;

· кадмій і олово для покриття елементів;

· свинець, мідь, алюміній для виготовлення прокладок.

Передача теплової енергії конвекцією

Конвективна тепловіддача

Мова йде про передачу тепла з поверхні твердого тіла в газ або рідину, які переміщуються відносно поверхні. Цей процес суттєво залежить від стану нагрітого середовища. Конвекція завжди супроводжується теплопровідністю

,

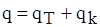де q- поверхнева густина теплового потоку;

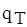- теплопровідна складова;

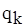 - конвективна складова.

Якщо швидкість переміщення V газу чи рідини відносно поверхні тіла падає до нуля, то 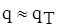. Якщо ж ця швидкість досягає високих значень, то 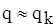. У більшості практичних задач .

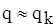Процес конвекції формально (математично) зводиться до процесу теплообміну (тіло - рідина). Цей процес називається конвективною тепловіддачею та виражається формулою Ньютона:

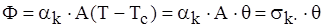, (1.13)

де А - площа поверхні тепловіддачі;

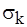- конвективна теплопровідність, ;

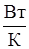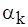- коефіцієнт конвективної тепловіддачі, .

Формула Ньютона виглядає як лінійна функція, але справа в тому, що коефіцієнт конвективної тепловіддачі складним чином суттєво залежить від багатьох теплофізичних та гідродинамічних факторів. Коефіцієнт конвективної тепловіддачі розглянемо як функцію

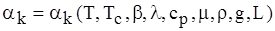, (1.14)

де 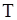 - температура тіла;

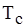 - температура середовища;

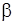 - коефіцієнт термічного розширення середовища;

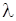 - теплопровідність середовища;

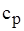 - теплоємність середовища;

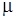 - коефіцієнт динамічної в’язкості середовища;

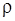 - густина середовища;

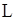 - визначальний розмір тіла;

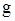 - прискорення земного тяжіння.

В залежності від конкретних умов (1.14) може набути досить простого вигляду. Теорія подібності дає ряд критеріїв, які дозволяють класифікувати задачу визначення αK по значеннях цих критеріїв. Формула (1.14) в залежності від конкретних умов набуває декількох характерних форм, кожна з яких значно простіша базової формули.