Стінки є досить розповсюдженими елементами конструкцій обчислювальної техніки. Тепловий опір стінок можна визначати незалежно від умов роботи конструкції та робочих режимів. Розглянемо найбільш типові випадки та виведемо розрахункові формули для визначення теплового опору.

Однорідна поперечна плоска стінка

На рис.1.2. зображена однорідна плоска стінка товщиною δ. Через неї в поперечному напрямку протікає однорідний тепловий потік Ф у напрямі зменшення температури; при цьому ti - температура лівої поверхні стінки, tj - температура правої поверхні стінки, ti > tj.

Теплове коло є тепловим опором Rij з температурними потенціалами на кінцях ti, tj. Формула (1.6) у даному випадку набуде вигляду:

.

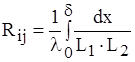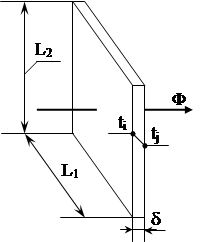а)                                                б)

Рис. 1.2. Однорідна поперечна плоска стінка (а) та її теплова модель (б)

Остаточно запишемо її так:

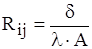. (1.8)

Отже, тепловий опір пропорційний товщині стінки δ і обернено пропорційний її площі А та теплопровідності матеріалу λ.

Циліндрична стінка

Нехай однорідний тепловий потік Ф напрямлений у напрямку зовнішньої стінки (рис.1.3).

Рис.1.3. Циліндрична стінка

Хоча теплове коло, як і в попередньому випадку, складається з одного теплового елемента Rij, розрахункова формула буде іншою. В даному випадку площа поверхні, через яку проходить тепловий потік Ф, є функцією 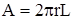. Тому формула (1.6) набуває вигляду

.

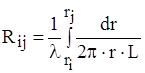Остаточно запишемо її так:

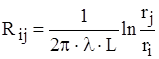. (1.9)

Поперечна багатошарова стінка

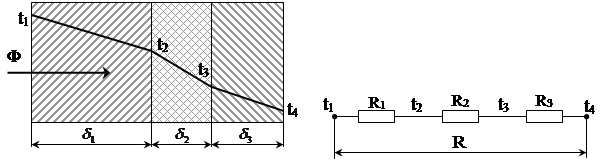
На рис.1.4 зображена поперечна стінка, що складається з трьох шарів. Незмінний однорідний тепловий потік Ф послідовно проходить через кожний шар як через однорідну поперечну стінку площею А.

а)                                                                   б)

Рис.1.4. Поперечна багатошарова стінка площею А (а) та її теплова модель (б)

Теплове коло є послідовним з’єднанням теплових опорів кожного шару. Тепловий опір всієї стінки визначається як сума теплових опорів елементів. У загальному випадку розрахункова формула набуває вигляду:

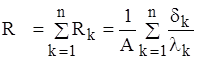. (1.10)

Поздовжня багатошарова стінка

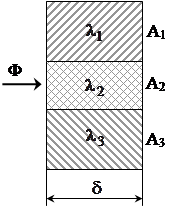
Всі шари стінки мають однакову товщину δ (рис.1.5).

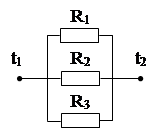а)                                                б)

Рис.1.5. Поздовжня багатошарова стінка (а) та її теплова модель (б)

Тепловий потік Ф розподіляється між кожним шаром стінки площею Аk. Кожний шар має свою теплопровідність матеріалу λk. Через поверхню площею Аk проходить тепловий потік Фk, при цьому 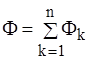. Теплове коло є паралельним з’єднанням теплових опорів кожного шару. Тепловий опір всієї стінки знайдемо по аналогії з визначенням опору електричного кола. Одержимо розрахункову формулу

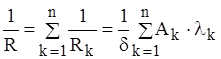. (1.11)