Для цепей сложной структуры использовалась запись уравнений в матричной форме. Матричная запись:
1) позволяет распространять формальным образом полученные уравнения на цепи любой сложной структуры;
2) систематизирует и упрощает процесс составления уравнений;
3) дает алгоритмы формирования уравнений с помощью ЭВМ; в случае сложных цепей составление уравнений «вручную» (без ЭВМ) требует значительных затрат времени.
Рассмотрим классические методы контурных и узловых уравнений. Вначале введем понятие графа цепи, описывающего свойства цепи, связанные с взаимным соединением ветвей, т. е. с геометрической структурой (топологией) схемы. Применение понятия графа позволяет записывать в матричной форме уравнения соединений, составляемые на основе законов Кирхгофа, и тем самым формировать уравнения разветвленных цепей с помощью ЭВМ.
Уравнения равновесия токов и напряжений, составленные по Законам Кирхгофа, как указывалось, линейными однородными уравнениями. Важное условие, которое должно обеспечиваться, состоит в линейной независимости уравнений. Ни одно уравнение не должно быть получено линейной комбинацией остальных уравнений. Общий систематический метод получения линейно независимых уравнений цепи основан также на привлечении понятий теории линейного графа, одного разделов математической дисциплины—топологии. К линейному графу приводит следующее соображение:
Уравнения равновесия токов и напряжений, составленные по законам Кирхгофа, определяются только схемами соединений ветвей, т. е. геометрической структурой цепи, и не зависят от вида и характеристик элементов, т. е. от физического содержания ветвей. Поэтому при составлении уравнений соединений удобно отвлекаться от вида и характеристик ветвей цепи, заменив их линиями. В результате для цепи рис. 3.1, а, составленной из любых двухполюсных элементов, получим линейный граф, показанный на рис. 3.1, б.

Граф является системой или совокупностью двух элементов—узлов (вершин), изображаемых точками, и ветвей (ребер), изображаемых отрезками линий, которые соединяют пары узлов. В предельном вырожденном случае граф может состоять только из одного узла.
Числа узлов и ветвей графа обозначим п y и n д. Поскольку каждому узлу и каждой ветви цепи сопоставляется узел и ветвь графа, граф цепи содержит всю информацию о соединениях и геометрических свойствах исходной цепи. На рис. 3.1, а, б соответственные узлы, а также ветви цепи и графа имеют одинаковые номера.
Граф, так же как и исходная цепь, может иметь различную структуру. Различают планарный (плоский) граф, если его можно изобразить на плоскости без пересечения ветвей (рис. 3.1,6), и не планарный (пространственный) граф, если при его изображении на плоском чертеже невозможно избежать пересечения ветвей (рис. 3.2, а). Полным называют граф, у которого каждая пара узлов соединена одной ветвью. Примером полного графа цепи может служить граф рис. 3.2, а.
Любую часть графа, элементы которой являются элементами исходного графа, называют подграфом. Подграф получают путем удаления (исключения) некоторых ветвей исходного графа.
Важным подграфом является путь графа, представляющий непрерывную последовательность ветвей, связывающую пару выбранных узлов, с прохождением каждого узла не более одного раза. Смежные ветви пути имеют общий узел, так что к каждому узлу присоединены две ветви, лишь к крайним узлам — по одной ветви.
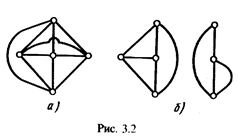
На рис. 3.1, б пути, связывающие узлы 1, 4, образованы ветвями 2-4, 5-6, 1, 2-3-5 и т. д. Если в заданном графе имеется хотя бы один путь между любой парой узлов, то граф называется связным—он соответствует цепи, элементы которой соединены только электрически. Граф рис. 3.1, б является примером связного графа, а рис. 3.2, б —несвязного: он состоит из двух раздельных частей, элементы которых могут иметь связь, например, через взаимную индуктивность.
Для составления уравнений соединений по законам Кирхгофа необходимо на всех ветвях графа стрелками указать положительные направления токов. В результате получается граф с ориентированными ветвями, называемый направленным графом токов цепи (рис. 3.1, б), ветви которого являются токами. Положительные полярности напряжений ветвей удобно принимать согласованными с положительными направлениями токов. Тогда в цепях, составленных из двухполюсных элементов, направленный граф напряжений, ребра которого являются напряжениями ветвей, будет совпадать с графом токов. Переход к направленному графу позволяет производить аналитическую запись структуры графа и подграфов в виде таблиц – матриц, называемых топологическими матрицами. Аналитическое представление графа необходимо для формирования уравнений сложной цепи с помощью ЭВМ.
Полное описание структуры направленного графа дает n уxn в - матрица соединений, nу строк которой являются порядковыми номерами узлов, nв столбцов – номерами ветвей. Элементами а i,j этой матрицы являются символы наличия или отсутствия ветви k, присоединенной к узлу i, которые принимаются равными +1 (—1) для выходящей из узла (входящей) ветви и 0, если ветвь не связана с узлом.
Для того чтобы записать матрицу соединений, достаточно для каждой ветви определить номера обоих соединяемых узлов i, j и заполнить клеточки на пересечениях строк i, j и столбца с номером ветви k значениями +1, — 1; в остальных клеточках должны быть проставлены нули. Для графа рис. 3.1,б получим полную матрицу соединений:

(3.1)
Так как каждая ветвь соединяет два узла—выходит из одного узла и входит в другой, то столбец матрицы состоит из двух ненулевых элементов +1, —1 (их сумма равна нулю), так что достаточно заполнить таблицу для ny-1 узлов, которая является редуцированной матрицей соединений А. Эту независимую матрицу можно получить из полной матрицы Аa вычеркиванием строки, соответствующей выбранному базисному узлу.
Приняв в качестве базисного узел 4 и соответственно вычеркивая четвертую строку в (3.1), получим редуцированную матрицу соединений:

(3.2)
Строка матрицы А показывает, какие ветви выходят из каждого независимого узла графа цепи (и входят в него), а столбец – к каким узлам присоединена ветвь.
В отличие от полной матрицы Аа у редуцированной матрицы соединений связного графа множество всех строк линейно независимо. Отсюда можно сделать вывод о том, что система уравнений равновесия токов в ny-1 узлах цепи линейно независима. Если ввести вектор токов пв, ветвей:
i=[i1, i2, … inв]Т, (3.3)
то систему независимых уравнений в nу -1 узлах по ЗТК в соответствии со смыслом матрицы А можно записать в виде:
Ai=0, (3.4)
где 0=[0 0 … 0]T - нулевой вектор размерности nу -1.
Для графа цепи рис. 3.1, б с матрицей соединений (3.2) имеем:

Транспонированная матрица соединений имеет вид:

(3.5)
Строка этой матрицы показывает, между какими узлами присоединена каждая ветвь.
Если задана матрица соединений, то всегда можно построить соответствующий граф. Для этого, расположив точки, обозначающие узлы, следует соединить их попарно ветвями. Номера и направление ветвей определяются ненулевыми элементами столбцов матрицы соединения.
Уравнения контурных токов
Метод контурных токов применим к цепям с планарным графом (рис. 3.3, а). В качестве переменных принимают замкнутые контурные токи, проходящие по ветвям, образующим все внутренние ячейки графа.
Если намечать контуры – периметры ячеек – по порядку, начиная с одного края цепи, то легко убедиться, что в каждый последующий контур вносится новая ветвь, не вошедшая в предыдущие контуры. Отсюда следует, что уравнения равновесия напряжений в таких контурах будут линейно независимы. Число внутренних ячеек равно nx=nв-ny+1.
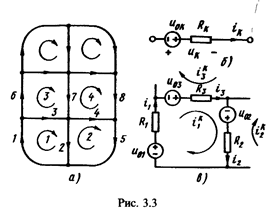
Каждой ячейке приписывается один контурный ток, замыкающийся по ветвям, образующим ячейку. Общее число переменных – контурных токов – равно числу ячеек. Направления всех контурных токов принимают одинаковыми – по часовой стрелке. Как видно из рис. 3.3, a, по каждой ветви цепи, за исключением периферийных ветвей, замыкаются два контурных тока, направленные в противоположные стороны. Запишем уравнения соединений.
1. Приравнивая нулю суммы напряжений ветвей всех независимых контуров (ячеек), имеем nх уравнений по ЗНК  .
.
2. Выражая ток каждой ветви через разность двух (в общем случае) замыкающихся по смежным контурам контурных токов, получим nв уравнений по ЗТК:
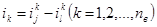 .
.
Как видно, токи всех ветвей, т. е. поведение всей цепи, полностью определяются nх контурными токами, число которых меньше числа ветвей.
Запишем уравнения ветвей. Положим для удобства, что выполнено преобразование всех источников тока и цепь содержит только источники напряжения. Примем для общности каждую ветвь состоящей из последовательного соединения резистивного элемента и источника напряжения (рис. 3.3,6). Уравнение такой составной ветви имеет вид:
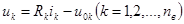 .
.
Для получения уравнений относительно выбранных переменных необходимо:
1) с помощью уравнений ветвей 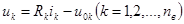 в уравнениях равновесия напряжений заменить напряжения всех ветвей токами;
в уравнениях равновесия напряжений заменить напряжения всех ветвей токами;
2) токи ветвей в получившейся системе заменить, согласно 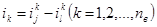 , контурными токами.
, контурными токами.
Получим уравнения для одной из ячеек, например первой (рис. 3.3, в), образованной тремя ветвями. Основным уравнением равновесия напряжений в первом контуре будет:
u1+u2+u3=0 (*)
Токи ветвей ячейки:
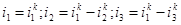 .(**)
.(**)
Уравнения ветвей:
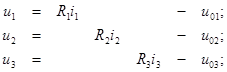 (***)
(***)
Из трех систем уравнений (*), (**), (***) необходимо получить уравнение, содержащее только искомые контурные токи. В соответствии со сказанным с помощью (***) заменяем в основном уравнении (*) напряжения на токи ветвей, которые затем выражаем через контурные токи согласно (**):
 ,
,
После группировки имеем:
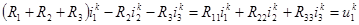
Первое слагаемое здесь представляет сумму напряжений всех резистивных ветвей контура только от собственного контурного тока в отсутствие токов других контуров (при их разрыве), а остальные слагаемые—напряжения ветвей контура от токов других контуров в отсутствие собственного контурного тока. В правую часть перенесены напряжения всех источников, входящих в контур.
Аналогичные уравнения получим для остальных контуров. Если число контуров равно п, то предположив для общности число ветвей каждой ячейки также равным п, можно записать систему уравнений контурных токов:

Коэффициент Rkk —собственное сопротивление контура, равное сумме сопротивлений всех ветвей ячейки, а коэффициент Rik=Rki (i<>k) – взаимное сопротивление контуров, равное сопротивлению общей для контуров i и k ветви, взятому с отрицательным знаком, которым учитываются встречные направления контурных токов в рассматриваемой ветви.
Каждое уравнение системы выражает условие равновесия напряжений ветвей контура – резистивных и источников напряжения (в правой части). Слагаемое на главной диагонали  дает напряжение всех резистивных ветвей только от собственного контурного тока, а слагаемое Рkjij=ukj - напряжение на взаимном сопротивлении контуров только от тока в j-м контуре.
дает напряжение всех резистивных ветвей только от собственного контурного тока, а слагаемое Рkjij=ukj - напряжение на взаимном сопротивлении контуров только от тока в j-м контуре.
Составление уравнений сводится к записи симметричной матрицы параметров контурных токов:

Вектора контурных напряжений источников, составляющие которых равны суммам напряжений источников в контурах:
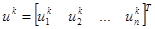
При введении вектора искомых контурных токов уравнения (3.10) в матричной форме можно записать в виде:
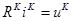 .
.
Дата: 2019-05-29, просмотров: 317.