Электрическую цепь, приближенно отображающую электро­магнитные процессы в реальном устройстве, составляют путем соответствующего соединения между собой рассмотренных двухполюсных элементов: сопротивления, индуктивности, ем­кости и источников сигнала. В общем случае отдельные элементы, а также отдельные участки цепи могут соединиться произвольно. В дипломной работе рассмотрены только соединение сопротивления и источника сигнала, в качестве которого используют ЭДС.

В результате получается электрическая схема, имеющая определенную геометрическую конфигурацию. На рис. 4 приложения показан пример схемы электрической цепи, составлен­ной из нескольких сопротивлений и источников ЭДС.

Основными понятиями, характеризующими геометрическую конфигурацию разветвленной цепи, являются ветвь и узел.

Под ветвью в общем случае понимают участок цепи с двумя выводами. Токи ветви принимают в качестве неизвестных переменных, характеризующих состояние цепи. Поэтому, что конкретно следует понимать под ветвью, зависит от выбора переменных цепи. Ветвью можно считать каждый элемент цепи. Но для уменьшения числа переменных за ветви иногда принимают также участки из последовательного соеди­нения отдельных элементов, токи которых имеют одно и то же значение, и участки из параллельного соединения отдельных элементов, напряжения на которых имеют одно и то же значение. При анализе схемы за ветвь принимается участок цепи между двумя узлами цепи.

Узел электрической цепи – это точка на схеме, в которой сходятся более двух ветвей [4]. Например, на рисунке №4 приложения – 4 узла.

Задача анализа электри­ческой цепи формулируется та­ким образом: Заданы схема электрической цепи со значения­ми всех ее элементов, а также напряжения источников, действующих в цепи. Требуется найти токи ветвей. В дальнейшем будем применять общие термины, назы­вая заданные напряжения источников функциями воз­буждения или сигналами, а искомые токи вет­вей, определяемые в результате анализа цепи, - реакциями. Следовательно, требуется найти реакции цепи на действие заданных сигналов.

Выводы – узлы или ветви, реакции которых необходимо найти, - называют выходными, а выводы, к которым при­соединены источники, - входными.

Программа предназначена для анализа любой линейной цепи произвольной конфигура­ции с любым конечным числом элементов.

Для определения искомых реакций – токов ветвей в общем случае – необходимо со­ставить уравнения цепи с помощью двух систем уравнений:

1) уравнений элементов, связывающих ток и напряже­ние каждого элемента, а также заданные напряжения. Уравнения элементов не зависят от схемы и геометрической конфигурации цепи, в которую входят элементы;

2) уравнений соединений, которые определяются только геометрической конфигурацией и способами соединений ветвей (элементов цепи) и не зависят от вида и характера элементов. Уравнения соединений устанавливают связи между токами и напряжениями отдельных элементов, входящих в цепь.

Уравнения соединений составляют па основе двух законов Кирхгофа, которые связывают токи ветвей, сходящихся в узлах, и напряжения ветвей, входящих в контуры; контуры представляют замкнутые пути, проходящие однократно через ряд ветвей и узлов.

Первый закон Кирхгофа, выражающий закон сохра­нения заряда, дает уравнение равновесия токов в узле цепи и формулируется так: в любой момент алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

.

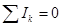Знак тока определяется выбором положительных направле­ний токов ветвей; токам, выходящим из узла, приписывают условно знак «-», а током, входящим в узел, - знак «+».

Второй закон Кирхгофа, выражающий закон сохра­нения энергии, дает уравнение равновесия напряжений в контуре и формулируется следующим образом: в любой момент алгебраическая сумма напряжений ветвей в контуре равна нулю

.

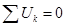Знак напряжения определяется выбором положительных полярностей напряжений ветвей: если при обходе контура перемещение происходит в сторону понижения или падения напряжения, то напряжению ветви условно приписывают знак «+», если в сторону повышения напряжения - знак «-».

Линейные цепи, составленные из элементов одного вида, например резистивных, описываются системами линейных ал­гебраических уравнений.

Применяя программу расчета линейных разветвленных электрических схем, необходимо лишь нарисовать схему, и ввести все значения сопротивлений и ЭДС. Все остальные преобразования, такие как выбор обхода контура, направления ЭДС, программа выполнит сама и выдаст конечный результат – значения токов в ветвях схемы.

Целью настоящей дипломной работы является создание математической модели и программы работающей по этой модели, позволяющей анализировать и расчитывать разветвленные электрические цепи постоянного тока, на основе использования законов Кирхгофа.

На основе проведенного литературного обзора я убедился, что в настоящее время существуют только программы, которые решают лишь уравнения созданные при анализе цепи, но не производят анализ самой цепи.

Глава 2. Пример. Результаты вычислений

Задача [3, №1.50]

Дано:

Е₁=120В; Е₂=60В; Е₃=140В;

R₁=1Ом; R₂=0,5Ом; R₃=0,4Ом; R₄=R₅=R₆=3Ом

Найти токи в ветвях.

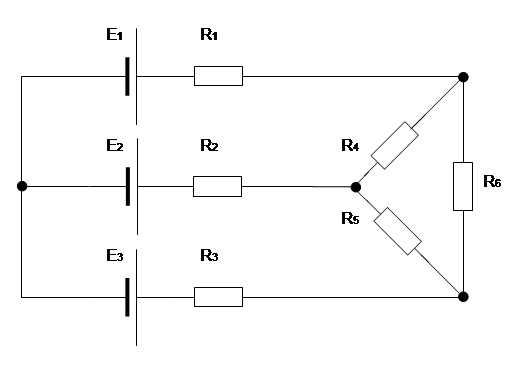Ответ задачи: I₁=6,8; I₂=30,9; I₃=24,1; I₄=12,6; I₅=18,3; I₆=5,8.

Схема для задачи:

Эквивалентная схема для программы:

Результат вычисления программы:

Ответ: I₁=6,83; I₂=30,88; I₃=24,05; I₄=12,57; I₅=18,31; I₆=5,74.

Как видно, программа дает более точный результат, чем тот, который предлагается для проверки правильности решения задачи.

Результаты вычислений выводятся в отдельном окне. (Рисунок №6 приложения).