Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Приднестровский Государственный Университет

Им. Т.Г. Шевченко

 

 

Физико-математический факультет

 

Кафедра общей физики и методики преподавания физики

Кафедра информатики и вычислительной техники

 

Дипломная работа

 

Математическое моделирование физических задач на ЭВМ

На примере расчета разветвленных цепей постоянного

тока основанного на использовании законов Кирхгофа

 

 

Выполнил:

Студент 506 группы

Коваленко А.С.

 

 

Научные руководители:

 

Кандидат

физико-математических

наук, доцент                                                                                 Цыпишка Д.И.

 

 

Кандидат

физико-математических

наук, доцент                                                                                  Брагарь Л.Ф.

 

 

Тирасполь, 2000г.

Содержание:

 

 

Введение....................................................................................................................................... 3

1. Напряжение и ток в электрической цепи................................................................................. 4

2. Резистивный элемент.............................................................................................................. 5

3. Источники................................................................................................................................ 6

Глава 1. Задача анализа разветвленной цепи.................................................................... 7

Глава 2. Пример. Результаты вычислений........................................................................... 9

Глава 3. Методика моделирования...................................................................................... 10

1. Линейный граф и матрица соединений................................................................................... 10

2. Уравнения контурных токов................................................................................................... 13

3. Алгоритм формирования узловых уравнений........................................................................ 16

Заключение................................................................................................................................ 17

Использованная литература................................................................................................. 18

Приложение................................................................................................................................ 19

Введение

 

Все электротехнические и радиотехнические устройства пред­ставляют собой электромагнитные устройства, главные про­цессы в которых подчиняются общим законам электромагне­тизма. В любом электромагнитном устройстве происходит движение электрических зарядов, неразрывно связанное с изменяющимся во времени и пространстве электромагнитным полем, двумя сторонами которого являются электрическое и магнитное поля.

Электромагнитные процессы сопровождаются взаимным преобразованием электромагнитной энергии в другие виды энергии. Точный анализ этих процессов, описываемых систе­мами уравнений в частных производных (уравнениями Макс­велла), - задача, трудно разрешимая даже в простейших слу­чаях. Но для инженерных расчетов и проектирования устройств необходим количественный анализ. Поэтому возникает потреб­ность в приближенных методах анализа, позволяющих с достаточной степенью точности решать широкий круг задач. Такие методы дает теория электрических цепей, которая для характеристики электромагнитных процессов вместо векторных величин теории поля, зависящих от пространственных коорди­нат и времени, вводит интегральные скалярные величины – ток и напряжение, являющиеся функциями времени.

Для приближенного учета процессов преобразования электромагнитной энергии в теории цепей вводят идеальные элементы с выводами или полюсами, через которые проходит электрический ток. Простейшими идеальными, базисными эле­ментами являются двухполюсные элементы с двумя полюсами или выводами – индуктивный, емкостный и резистивный эле­менты, учитывающие накопление энергии в магнитном и электрическом полях и необратимое преобразование электро­магнитной энергии в другие виды энергии. Для учета преобра­зования энергии неэлектрической природы (химической, меха­нической, тепловой и т. д.) в электромагнитную энергию вводят элемент с двумя выводами, называемый источником. Наряду с указанными вводят четырехполюсные и многополюсные эле­менты в общем случае с n выводами.

Соединяя между собой соответствующим образом эти идеальные элементы, получают электрическую цепь, приближенно отображающую электромагнитные процессы в каком-либо устройстве по отношению к интересующим выводам.

Теория цепей применима к большому числу устройств, в которых представляют интерес процессы в отдельных точках – выводах.

В настоящее время существуют методы и средства расчета радиотехнических цепей на основе математических моделей, представляющие собой в общем случае системы нелинейных дифференциальных уравнений. Одним из многих таких средств является программа, предложенная в [1], которая представляет собой реализацию математической модели расчета цепей постоянного тока. Программа работает следующим образом: пользователь вводит все данные для расчета цепи, самостоятельно производя анализ цепи, т.е. он вводит количество узлов, количество ветвей с элементами, находящимися на них и номиналы этих элементов. Програма решает получающиеся при этом линейные уравнения и выводит результат вычислений.

Недостатком указанных выше программных средств является отсутствие автоматизированного построения разветвленных цепей, ввода элементов, выбора направления обхода контуров и токов в ветвях по введенной принципиальной схеме. Кроме этого существующие программы не позволяют непосредственно при расчетах проводить анализ полученных результатов, в динамике изменять параметры компонентов.

В связи с этим целью дипломной работы является: разработка математической модели и программы анализа и расчета цепей постоянного тока, автоматического выбора направления обхода контура и направления токов в ветвях цепи, и выводить результаты вычислений.

В данной дипломной работе рассматривается метод расчета и анализа линейных разветвленных цепей содержащих резистивные элементы и источники ЭДС с постоянными пара­метрами элементов основанный на использовании законов Кирхгофа.

 

Резистивный элемент

 

Под резистивным элементом электрической цепи или активным сопротивлением понимают идеализированный эле­мент, в котором происходит только необратимое преобразование электромагнитной энергии в теплоту или другие виды энергии, а запасание энергии в электрическом и магнитном полях от­сутствует.

По свойствам к этому идеальному элементу довольно близки такие реальные устройства, как угольные сопротивления, реостаты, лампы накаливания при относительно небыстрых изменениях токов.

Условное графическое обозначение резистивного элемента Представлено на рис. 1.2, а, где указаны принятые положитель­ные направления напряжения и тока.

Основное уравнение элемента, связывающее ток и напряжение, так называемая вольт-амперная характеристика, определяется законом Ома, который устанавливает пропорциональ­ность между напряжением и током:

U=RI, I=GU               (1.3)

Коэффициент пропорциональности в первом выражении (1.3), равный отношению напряжения и тока, является электрическим сопротивлением:

R=U/I                            (1.4)

Численно сопротивление равно напряжению на элементе при токе в 1 А. Значение сопротивления выражается в омах.

Обратная величина – отношение тока к напряжению – представляет собой электрическую проводимость:

G=I/U=1/R.               (1.5)

В теории линейных электрических цепей сопротивление и проводимость принимают постоянными, не зависящими от тока, напряжения и других величин. В реальных элементах это допущение, так же как и допущение отсутствия запасания энергии, выполняется приближенно.

Источники

 

Под источником в теории цепей понимают элемент, питающий цепь электромагнитной энергией. Эта энергия по­требляется пассивными элементами цепи – запасается в индуктивностях и емкостях и расходуется в активном сопротивлении.

Напряжения источников, представляющие задан­ные функции времени, называют также приложенными к цепи или возбуждающими цепь сигналами. Примерами реальных источников электромагнитной энергии могут служить генераторы постоянных, синусоидальных и импульсных сигналов разнообразной формы, сигналы, полу­чаемые от различного рода датчиков, антенн радиоприемных устройств и т. д. Эти источники сигналов либо являются первичными источниками, в которых происходит непосредст­венное преобразование энергии неэлектромагнитной природы (механической, химической, тепловой и т. д.) в электромагнит­ную энергию, либо получают питание от первичных источников. Источник является актив­ным элементом.

Для анализа цепей вводят идеализированный источник напряжения, который учитывает главные свойства реального источника.

Источник напряжения. Под источником напряжения понимают такой элемент с двумя выводами (полюсами), напряжение между которыми задано в виде некоторой функции времени независимо от тока, отдаваемого во внешнюю цепь.

 

 

а)                 б)

Рисунок 1.3.

Наиболее часто применяемые условные графические обо­значения источника напряжения представлены на рис. 1.3, а и б, где принятая положительная полярность напряжения источника указывается либо стрелкой внутри кружочка, либо большой и малой чертами, малая соответствует знаку «-», а большая - «+». Поскольку положительную полярность напряжения усло­вились обозначать знаками «+», «-», для источника напряже­ния в программе применено обозначение, показанное на рис. 1.3, б.

 

Глава 2. Пример. Результаты вычислений

Задача [3, №1.50]

Дано:

Е₁=120В; Е₂=60В; Е₃=140В;

R₁=1Ом; R₂=0,5Ом; R₃=0,4Ом; R₄=R₅=R₆=3Ом

Найти токи в ветвях.

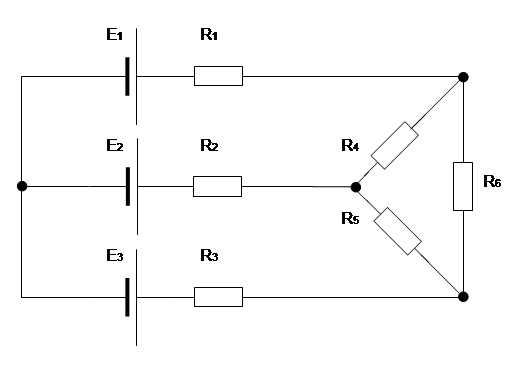Ответ задачи: I₁=6,8; I₂=30,9; I₃=24,1; I₄=12,6; I₅=18,3; I₆=5,8.

Схема для задачи:

 

 

Эквивалентная схема для программы:

 

Результат вычисления программы:

Ответ: I₁=6,83; I₂=30,88; I₃=24,05; I₄=12,57; I₅=18,31; I₆=5,74.

 

Как видно, программа дает более точный результат, чем тот, который предлагается для проверки правильности решения задачи.

Результаты вычислений выводятся в отдельном окне. (Рисунок №6 приложения).

Уравнения контурных токов

 

Метод контурных токов применим к цепям с планарным графом (рис. 3.3, а). В качестве переменных принимают замкну­тые контурные токи, проходящие по ветвям, образующим все внутренние ячейки графа.

Если намечать контуры – периметры ячеек – по порядку, начиная с одного края цепи, то легко убедиться, что в каждый последующий контур вносится новая ветвь, не вошедшая в предыдущие контуры. Отсюда следует, что уравнения равно­весия напряжений в таких контурах будут линейно независимы. Число внутренних ячеек равно n_x=n_в-n_y+1.

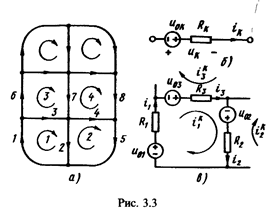
Каждой ячейке при­писывается один кон­турный ток, замыкаю­щийся по ветвям, об­разующим ячейку. Об­щее число перемен­ных – контурных токов – равно числу ячеек. Направления всех контурных токов принимают одинаковыми – по часовой стрел­ке. Как видно из рис. 3.3, a, по каждой ветви цепи, за исключением периферийных ветвей, замыкаются два контурных тока, направленные в противоположные стороны. Запишем уравнения соединений.

1. Приравнивая нулю суммы напряжений ветвей всех неза­висимых контуров (ячеек), имеем n_х уравнений по ЗНК .

2. Выражая ток каждой ветви через разность двух (в общем случае) замыкающихся по смежным контурам контурных токов, получим n_в уравнений по ЗТК:

.

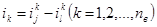Как видно, токи всех ветвей, т. е. поведение всей цепи, полностью определяются n_х контурными токами, число кото­рых меньше числа ветвей.

Запишем уравнения ветвей. Положим для удобства, что выполнено преобразование всех источников тока и цепь содержит только источники напряжения. Примем для общности каждую ветвь состоящей из последовательного соединения резистивного элемента и источника напряжения (рис. 3.3,6). Уравнение такой составной ветви имеет вид:

.

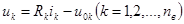Для получения уравнений относительно выбранных перемен­ных необходимо:

1) с помощью уравнений ветвей 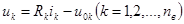 в уравнениях равновесия напряжений заменить напряжения всех ветвей токами;

2) токи ветвей в получившейся системе заменить, согласно 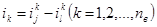, контурными токами.

Получим уравнения для одной из ячеек, например первой (рис. 3.3, в), образованной тремя ветвями. Основным уравнени­ем равновесия напряжений в первом контуре будет:

u₁+u₂+u₃=0 (*)

Токи ветвей ячейки:

.(**)

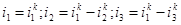Уравнения ветвей:

 (***)

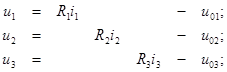Из трех систем уравнений (*), (**), (***) необходимо получить уравнение, содержащее только искомые контурные токи. В соответствии со сказанным с помощью (***) заменяем в основном уравнении (*) напряжения на токи ветвей, которые затем выражаем через контурные токи согласно (**):

,

  После группировки имеем:

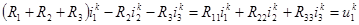
Первое слагаемое здесь представляет сумму напряжений всех резистивных ветвей контура только от собственного контурного тока в отсутствие токов других контуров (при их разрыве), а остальные слагаемые—напряжения ветвей контура от токов других контуров в отсутствие собственного контурного тока. В правую часть перенесены напряжения всех источников, входящих в контур.

Аналогичные уравнения получим для остальных контуров. Если число контуров равно п, то предположив для общности число ветвей каждой ячейки также равным п, можно записать систему уравнений контурных токов:

 

Коэффициент R_kk —собственное сопротивление контура, рав­ное сумме сопротивлений всех ветвей ячейки, а коэффициент R_ik=R_ki (i<>k) – взаимное  сопротивление контуров, равное сопротивлению общей для контуров i и k ветви, взятому с отрицательным знаком, которым учитываются встречные на­правления контурных токов в рассматриваемой ветви.

Каждое уравнение системы выражает условие равно­весия напряжений ветвей контура – резистивных и источников напряжения (в правой части). Слагаемое на главной диагонали  дает напряжение всех резистивных ветвей только от собственного контурного тока, а слагаемое Р_kji_j=u_kj - напря­жение на взаимном сопротивлении контуров только от тока в j-м контуре.

Составление уравнений сводится к записи симметричной матрицы параметров контурных токов:

 

Вектора контурных напряжений источников, составляющие которых равны суммам напряжений источников в контурах:

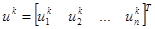
При введении вектора искомых контурных токов уравнения (3.10) в матричной форме можно записать в виде:

.

 

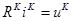Заключение

 

 

  Таким образом в настоящей дипломной работе:

· проведен литературный обзор по моделированию процессов в радиотехнических цепях, методов и средств расчетов токов и направлений в них;

· построена математическая модель разветвленной цепи постоянного тока;

· на языке программирования Турбо Паскаль версии 7.0. в удобном графическом интерфейсе разработана программа построения и анализа электрической схемы цепи постоянного тока;

· приведены методические пояснения при работе с разработанной программой, а также расчетов и анализа электрических цепей;

· программа допускает без принципиальных изменений расширение её функциональных возможностей для расчетов цепей переменного тока, а также моделирования и анализа электромагнитных полей;

· результаты настоящей дипломной работы могут быть использованы в учебном процессе, при разработке электронной аппаратуры в научных лабораториях и на производстве.

        

  В заключение хочу выразить благодарность своим научным руководителям: Цыпишка Дмитрию Ивановичу, Брагарь Луке Федеровичу и заведующиему кафедрой кафедрой общей физики и методики преподавания физики Стамову Ивану Григорьевичу, за методическую помощь, оказанную при написании дипломной работы.

 

Использованная литература

 

1. К.С. Демирчан, П.А. Бутырин. Моделирование и машинный расчет электрических цепей. М., «Высшая школа», 1988г.

2. В. Нерретер. Расчет электрических цепей на ПЭВМ. М., «Энергоатомиздат», 1991г.

3. Пантюшин В.С. Сборник задач по электротехнике и основам электронники. М., «Высшая школа», 1979г.

4. П.Н. Махтанов. Основы анализа электрических цепей. Линейные цепи. М., «Высшая школа», 1990г.

5. «Электротехника». Под редакцией проф. В.С. Пантюшина. М., «Высшая школа», 1976г.

6. В.Г. Абрамов, Н.П. Трифонов, Г.Н. Трифонова. «Введение в язык Паскаль». М., «Наука», 1988г.

7. Ж.Джонс, К. Харроу. «Решение задач в системе Турбо Паскаль». М., «Финансы и статистика», 1991г.

8. К. Боон. «Паскаль для всех». М., «Энергоиздат», 1988г.

9. Д. Прайс. «Программирование на языке Паскаль». Практическое руководство. М., «Мир», 1987г.

 

 

Приложение

 

I. Рисунки с видами экрана при работе с программой....................................................... 20

Рисунок №1. Общий вид экрана...................................................................................................... 20

Рисунок №2. Меню – Файл.............................................................................................................. 21

Рисунок №3. Открытие файла, сохраненного на диске.................................................................. 22

Рисунок №4. Вид экрана с изображением схемы........................................................................... 23

Рисунок №5. Вывод результата вычисления токов в ветвях схемы.............................................. 24

Рисунок №6. Просмотр направления токов в ветвях схемы.......................................................... 25

Рисунок №7. Вид экрана при сохранении схемы в файл................................................................. 26

Рисунок №8. Меню – Окно.............................................................................................................. 27

Рисунок №9. Окно помощи выводимое на экран при нажатии клавиши F1.................................... 29

II. Листинг программы на языке Паскаль............................................................................... 30

1. Основная программа.................................................................................................................. 30

2. Модуль с библиотекой элементов.............................................................................................. 36

3. Модуль вычисления токов ветвей............................................................................................... 48

 

Рисунок №1. Общий вид экрана.

 

Меню

                   Меню элементов

                                                                  Рабочее поле

                                                                                                     Указатель мыши

 

 

Строка статуса

                              Индекатор свободной памяти
Рисунок №2. Меню – Файл.

 

Меню – Файл

 

 

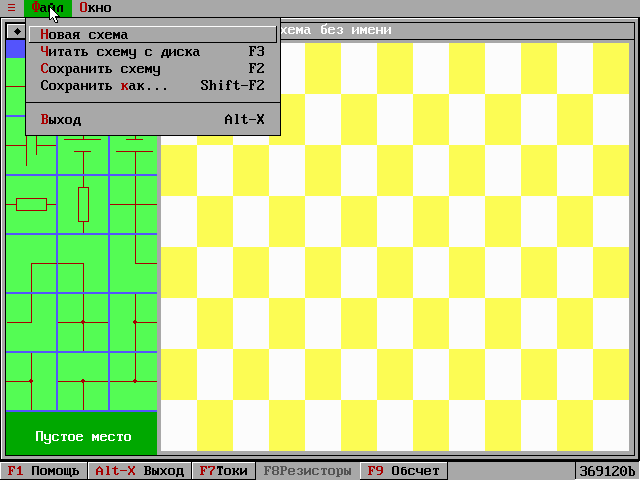
Рисунок №3. Открытие файла, сохраненного на диске.

 

Открытие файла со схемой

 

 

Рисунок №4. Вид экрана с изображением схемы.

 

 

Изображение схемы

 

Расчет схемы

Рисунок №5. Вывод результата вычисления токов в ветвях схемы.

 

Результаты вычислений

 

 

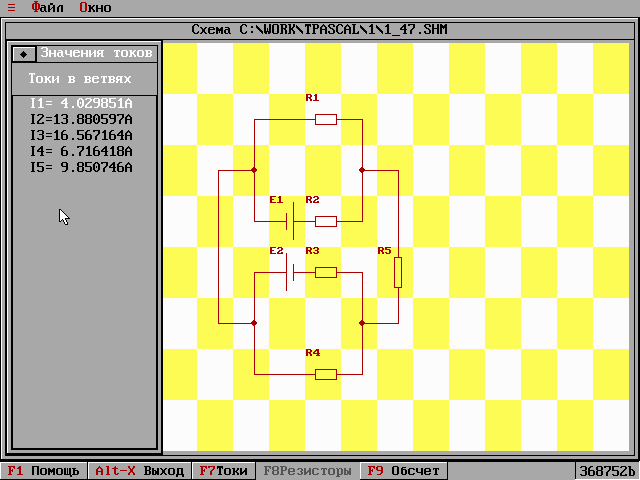
Токи

       Резисторы
Рисунок №6. Просмотр направления токов в ветвях схемы.

 

 

Значения токов

 

Направления токов

 

 

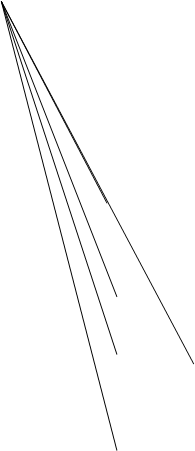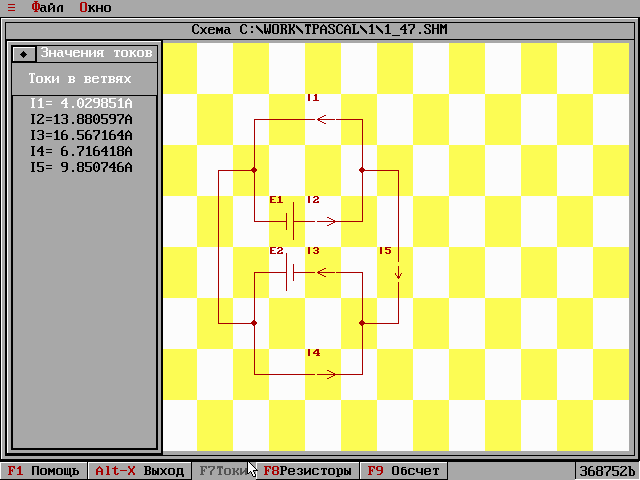
Рисунок №7. Вид экрана при сохранении схемы в файл.

 

 

Сохранение схемы

 

 

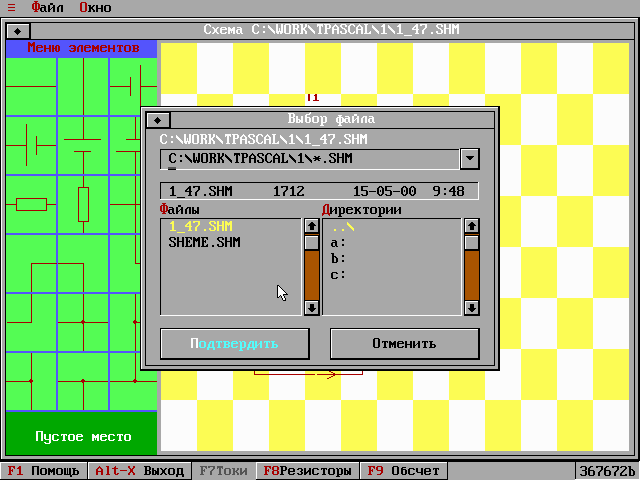
Рисунок №8. Меню – Окно.

 

 

Работа с окнами

 

 

Рисунок №9. Вид экрана при закрытии всех окон.

 

 

Указатель мыши

 

                              Меню

 

 

Строка статуса

                              Информация о свободной памяти
Рисунок №10. Окно помощи выводимое на экран при нажатии клавиши F1.

 

Закрытие окна

                              Окно с помощью программы

 

 

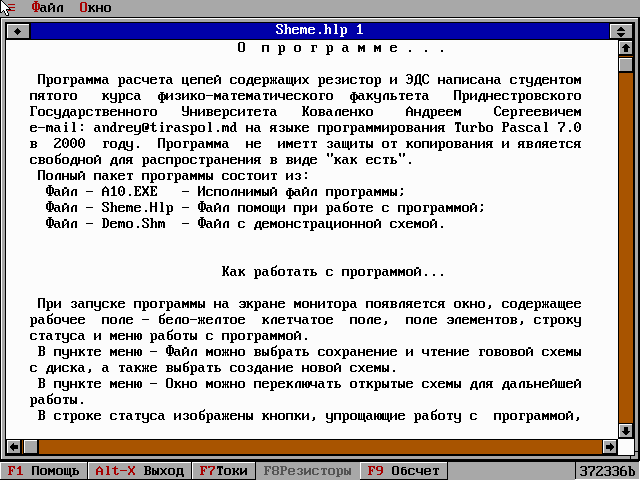
Горизонтальный скролинг

                                                 Вертикальный скролинг

II. Листинг программы на языке Паскаль.

 

Основная программа

 

Program UzPotenc; {Метод узловых потенциалов}

{$F+,O+,X+,V-,R-,I-,S-}

Uses

Crt, Applic1, Objects, Drivers, Dialogs, Views, Menus, App, StdDlg,

Fonts, HelpFile, MsgBox, TxtRead, WInDows, PalObj, Grv16, DemoHlp,

Types2;

Type TNewApp=Object(TMyApp)

  Procedure ReCounte; Virtual;

End;

Var MyApp:TNewApp;

Type

PMyCollection=^TMyCollection;

TMyCollection=Object(TCollection)

  Procedure FreeItem(Item:poInter); Virtual;

End;

 

Procedure CurView; {Просмотр значений токов}

Var R,R1:TRect;

   D:PDialog;

 L:PListBox;

 C:PMyCollection;

Sb:PScrollBar;

 i:Integer;

 s:String;

Begin

Sb:=Nil;

MyApp.ShemeWInDow^.GeTextentWIn(R);

R.B.X:=R.A.X+(R.B.X-R.A.X) Div 4;

D:=New(PDialog,Init(R,'Значения токов'));

D^.GeTextentWIn(R);

Inc(R.A.Y,CurrentFont^.Height*2);

R1.Copy(R);

R1.A.X:=R1.B.X-CurrentFont^.Width*2;

If RCount>(R.B.Y-R.A.Y) Div CurrentFont^.Height

Then

Begin

Sb:=D^.StAndardScrollBar(sbVertical+sbHAndleKeyBoard);

End;

C:=New(PMyCollection,Init(RCount,1));

For i:=1 To RCount Do

Begin

Str(abs(Currents[i]):9:6,s);

If i Div 10>0

Then C^.Insert(NewStr('I'+IntToStr(i)+'='+s+'A'))

Else C^.Insert(NewStr(' I'+IntToStr(i)+'='+s+'A'))

End;

L:=New(PListBox,Init(R,1,Sb));

L^.NewList(C);

D^.Insert(L);

R.B.Y:=R.A.Y;

Dec(R.A.Y,CurrentFont^.Height*2);

D^.Insert(New(PLabel,Init(R,' Токи в ветвях',L)));

DeskTop^.Insert(D);

 End;

 

Procedure TNewApp.ReCounte;{Обсчет}

Var

i,j,k,l,m,Ii,Sizex,Index:Integer;

A:TElAr;

f1,f2:Boolean;

Ratio:Real;

 

Function Vetv1(Ai,Aj,Ad:Integer):Boolean;

{Функция сохраняет в A ветвь от элемента (Ai,Aj) в направлении Ad (0-Up,1-Down,2-Left,3-Right и возвращает TRUE, если она содержит элементы}

Var i,j,k,l:Integer;

Flag1,Flag2:Boolean;

Begin

Flag1:=True;

Flag2:=False;

With A[Index] Do

Begin

Str:=Ai; Col:=Aj;

Num:=Sheme[Ai,Aj,2];

Typ:=Sheme[Ai,Aj,1];

End;

Inc(Index);

Case Ad Of

0: Begin i:=Ai+1; j:=Aj-1;   End;

1: Begin i:=Ai-1; j:=Aj+1; End;

2: Begin i:=Ai-1;   j:=Aj+1; End;   

3: Begin i:=Ai+1;   j:=Aj-1; End;

End;

While Flag1 And (i>0) And (j>0) And (i<=nS) And (j<=mS) And Not

    (Sheme[i,j,1] In [0,14..18]) Do

Begin

If Sheme[i,j,1] In [3..8]

Then

  Begin

   Flag2:=True;

   With A[Index] Do

    Begin

     Str:=i;

     Col:=j;

     Num:=Sheme[i,j,2];

     Typ:=Sheme[i,j,1];

     Case Ad Of

      0:Dir:=Typ In [5,8];

      1:Dir:=Typ=6;

      2:Dir:=Typ=4;

      3:Dir:=Typ In [3,7];

     End;

    End;

   Inc(Index);

  End;

Case Ad Of

0: Case Sheme[i,j,1] Of

     2,5,6,8,9 : Dec(i);

     10   : Begin Inc(j); Ad:=3; End;

     11   : Begin Dec(j); Ad:=2; End;

     Else Flag1:=False;

    End;

1: Case Sheme[i,j,1] Of

     2,5,6,8,9 : Inc(i);

     12   : Begin Inc(j); Ad:=3; End;

     13   : Begin Dec(j); Ad:=2; End;

     Else Flag1:=False;

    End;

2: Case Sheme[i,j,1] Of

     1,3,4,7,9 : Dec(j);

     10   : Begin Inc(i); Ad:=1; End;

     12   : Begin Dec(i); Ad:=0; End;

     Else Flag1:=False;

    End;

3: Case Sheme[i,j,1] Of

     1,3,4,7,9 : Inc(j);

     13   : Begin Dec(i); Ad:=0; End;

     11   : Begin Inc(i); Ad:=1; End;

     Else Flag1:=False;

    End;

End;

End;

If Sheme[i,j,1] In [14..18]

Then

Begin

With A[Index] Do

  Begin

   Str:=i;

   Col:=j;

   Num:=Sheme[i,j,2];

   Typ:=Sheme[i,j,1];

  End;

Inc(Index);

With A[Index] Do

  Begin

   Str:=0;

   Col:=0;

   Num:=0;

   Typ:=0;

  End;

Inc(Index);

End;

If Not Flag2

Then

Begin

For k:=1 To NoDecount Do

  If (Nodes[k,1]=i) And (Nodes[k,2]=j)

   Then l:=k;

NNum[l]:=NNum[Ii]; {Исключение накоротко замкнутых ветвей}

End;

Vetv1:=Flag2;

End;

 

Function ElEqu(Var Src,Dst:TEl):Boolean; {Returns TRUE, If Src=Dst}

Begin

With Src Do

ElEqu:=(Str=Dst.Str)And(Col=Dst.Col)And(Typ=Dst.Typ)And(Num=Dst.Num);

End;

 

Function IsDiv(Var Src:TEl):Boolean; {Returns TRUE, If Src - Divider}

Begin

With Src Do

IsDiv:=(Str=0)And(Col=0)And(Typ=0)And(Num=0);

End;

 

Function NextDiv(i:Integer):Integer; {Поиск след. разд. элемента в массиве}

Begin

Repeat

Inc(i);

Until (i>Sizex) Or IsDiv(A[i]);

If i<=Sizex

Then NextDiv:=i

End;

 

Function PrevDiv(i:Integer):Integer; {Поиск пред. разд. элемента в массиве}

Begin

Repeat

Dec(i);

Until (i<1) Or IsDiv(A[i]);

If i>=1

Then PrevDiv:=i

Else PrevDiv:=0;

End;

Begin

For i:=1 To nS*mS Div 2 Do

For j:=1 To nS*mS Div 2 Do

 Equals[i,j]:=0;

For Ii:=1 To NoDecount Do

NNum[Ii]:=Ii;

Index:=1;

For Ii:=1 To NoDecount Do

Begin

Case Sheme[Nodes[Ii,1],Nodes[Ii,2],1] Of

14:Begin

    Vetv1(Nodes[Ii,1],Nodes[Ii,2],0); Vetv1(Nodes[Ii,1],Nodes[Ii,2],1);

   End;

15:Begin

    Vetv1(Nodes[Ii,1],Nodes[Ii,2],0); Vetv1(Nodes[Ii,1],Nodes[Ii,2],1);

   End;

16:Begin

    Vetv1(Nodes[Ii,1],Nodes[Ii,2],0); Vetv1(Nodes[Ii,1],Nodes[Ii,2],1);

   End;

17:Begin

    Vetv1(Nodes[Ii,1],Nodes[Ii,2],1); Vetv1(Nodes[Ii,1],Nodes[Ii,2],2);

   End;

18:Begin

    Vetv1(Nodes[Ii,1],Nodes[Ii,2],0); Vetv1(Nodes[Ii,1],Nodes[Ii,2],2);

   End;

End;

End;

Sizex:=Index-1;

{Оставляет нужные ветви}

i:=1;

While i<=Sizex Do

Begin

j:=0;

f1:=True;

While (i+j<=Sizex) And f1 Do

Begin

k:=NextDiv(i+j);

If ElEqu(A[k-1],A[i])And ElEqu(A[k-2],A[i+1])

  Then

   Begin

    f1:=False;

    l:=PrevDiv(k);

    For m:=0 To Sizex-k Do

     A[l+m]:=A[k+m];

    Sizex:=Sizex-(k-l);

    i:=NextDiv(i)+1;

    If i=1

     Then i:=Sizex+1;

   End

  Else

   j:=k-i;

End;

End;

i:=0;

{Исключает пустые ветви}

While i<=Sizex Do

Begin

j:=NextDiv(i);

If j-i=3

Then

Begin

  For k:=1 To Sizex-j Do

End;

If j<>0

Then i:=j

Else i:=Sizex+1;

End;

{Считаем сколько узлов с учётом соединений}

NCount:=NoDecount;

For i:=1 To NoDecount Do

If NNum[i]<>i

Then Dec(NCount);

If NCount<>NoDecount

Then

For i:=1 To NoDecount Do

Begin

j:=0;

For k:=1 To NoDecount Do

  If NNum[k]=i

   Then j:=1;

If j=0

  Then

   For k:=1 To NoDecount Do

    If NNum[k]>i

     Then Dec(NNum[k]);

End;

i:=1;

j:=0;

Repeat

Inc(j);

k:=NextDiv(i);

With Brunches[j] Do

Begin

AEDS:=0;

ARes:=0;

For l:=i To k Do

With A[l] Do

   Case Typ Of

    3..6: If Dir

           Then EDS:=AEDS+EDS[Str,Col]

           Else EDS:=AEDS-EDS[Str,Col];

    7..8: ARes:=ARes+abs(Res[Str,Col]);

   End;

FromN:=NNum[A[i].Num];

If k<>0

Then

  Begin

   ToN:=NNum[A[k-1].Num];

   i:=k+1;

  End

Else

  Begin

   ToN:=NNum[A[Sizex-1].Num];

   i:=Sizex+1;

  End;

End;

Until i>Sizex;

BrunchCount:=j;

{Заполняем систему}

For i:=1 To BrunchCount Do

With Brunches[i] Do

Begin

Equals[FromN,FromN]:=Equals[FromN,FromN]+1/ARes;

Equals[ToN,NCount+1]:=Equals[ToN,NCount+1]+AEDS/ARes;

End;

{Решаем систему}

For i:=2 To NCount Do

Begin

Ratio:=Equals[i,i];

For j:=2 To NCount+1 Do

Equals[i,j]:=Equals[i,j]/Ratio;

For k:=2 To NCount Do

If k<>i

For i:=1 To NCount+1 Do

Begin

Equals[1,i]:=0;

Equals[i,1]:=0;

End;

{После решения расставляем токи}

For i:=1 To RCount Do

Begin

j:=1;

While (j<=Sizex) And Not ((A[j].Typ In [7,8]) And (A[j].Num=i)) Do

Inc(j); k:=0; l:=j;

Repeat

k:=k+1; j:=PrevDiv(j);

Until j=0;

With Brunches[k] Do

Begin

Currents[i]:=(AEDS-Equals[ToN,NCount+1]+Equals[FromN,NCount+1])/ARes;

If Not A[l].Dir

  Then Currents[i]:=-Currents[i];

End;

End;

CurView;

 End;

 

Procedure TMyCollection.FreeItem;

 Begin

If Item<>Nil

Then DisposeStr(PString(Item));

 End;

 

BEGIN

 MyApp.Init;

 MyApp.Run;

 MyApp.Done;

END.

Приднестровский Государственный Университет

Им. Т.Г. Шевченко

 

 

Физико-математический факультет

 

Кафедра общей физики и методики преподавания физики