а) Рассмотрим удлинения
dr - в отсчетной конфигурации, dR - в текущей конфигурации
dR = dr × 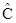 ;
; 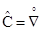 R (
R (  = ek (…),k / Hk)
= ek (…),k / Hk)
R = r + u
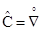 (r + u) =
(r + u) = 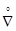 r +
r + 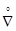 u =
u = 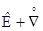 u
u
Рассмотрим относительное удлинение
(½dR½-½dr½) /½dr½ = e; ½dR½ = dS; ½dr½ = ds;
dS2 - ds2 = dR × dR - dr × dr = dr × 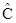 × dr ×
× dr × 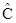 - dr × dr =
- dr × dr =
= dr × 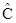 ×
×  × dr - dr ×
× dr - dr × 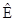 × dr = dr (
× dr = dr ( 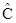 ×
×  - ×
- × 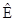 ) × dr =
) × dr =
= 2dr × 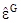 × dr;
× dr; 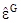 = 0,5 (
= 0,5 ( 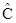 ×
×  -
- 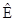 ) - тензор деформаций Грина
) - тензор деформаций Грина
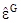 = 0,5 [ (
= 0,5 [ ( 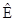 +
+  u) (
u) ( 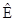 +
+ 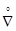 uT) -
uT) - 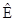 ] = 0,5 (
] = 0,5 ( 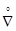 u +
u + 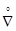 uT +
uT + 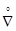 u ×
u × 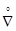 uT)
uT)
dr = e ds ® e = dr /½dr½ - единичный вектор
dS2 - ds2 = 2ds2 e×eG × e
(dS2 - ds2) /ds2= (dS/ds) 2 - 1 = 2e×eG×e
dS/ds = (1 + 2e×eG×e) 1/2;
ee = (dS - ds) /ds = (1 + 2e×eG×e) 1/2 - 1 - удлинение
Пусть e = e1;  = (1+2
= (1+2 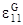 ) 1/2 - 1 = 1 +
) 1/2 - 1 = 1 + 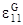 + … - 1 =
+ … - 1 = 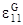 » e11
» e11
e = 0,5 (Ñu +ÑuT) - линейный тензор деформаций Коши.
Деформации сдвига
Выделим два прямолинейных волокна, направление которых определяется единичными векторами m1 и m2
dr1 = m1ds1; dr2 = m2ds2;
dsi = ½dri½ - длины элементов волокон до деформаций
Деформации сдвига характеризуется изменением угла q12
cos q12 - cos Q12 = (dr1× dr2) / (ds1× ds2) - (dR1× dR2) / (dS1× dS2) =
= m1 × m2 - [ (dr1× 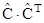 × dr2) / ds1 (1+em1) ds2 (1+em2)] =
× dr2) / ds1 (1+em1) ds2 (1+em2)] =
= m1 × m2 - m1× 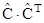 × m2 = m1× (
× m2 = m1× ( 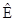 -
- 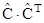 ) × m2 = - 2m1×
) × m2 = - 2m1× 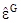 × m2;
× m2;
Пусть m1 = e1; m2 = e2; m1 × m2 = 0
cos q12 = 0 0 - cos Q12 = -2 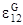
cos Q12 = cos (p/2 - g12) = 2 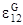 = sin g12 = g12
= sin g12 = g12
g12 - угол сдвига; g12 » e12, если g12 - небольшой
Повороты
Рассмотрим материальное волокно dr = e ds
w = (dr ´ dR) / (½dr½×½dR½) - вектор поворота материального волокна
½w½= sin j
w - нормаль, относительно которой происходит поворот
w = (dr ´ (dr × 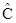 )) / (ds×ds (1 + ee)) = e ´ (e×
)) / (ds×ds (1 + ee)) = e ´ (e× 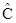 ) =
) =
= e ´ [e × ( 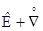 u)] = e ´ e + e ´ (e ×
u)] = e ´ e + e ´ (e × 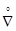 u) = e ´ (e ×
u) = e ´ (e × 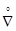 u)
u)
Пусть e = et - базисные вектора t = 1,2,3
wt - вектор поворота материального волокна t
wt = et ´ (et × 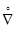 u) = et ´ (et × ukj ek ej) =
u) = et ´ (et × ukj ek ej) =
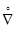 u = ukj ek ej
u = ukj ek ej  = et ´ (ukj dtk ej) = et ´ utj ej =
= et ´ (ukj dtk ej) = et ´ utj ej =
= utj 'tjk ek = wtk ek = wt, где wtk = utj 'tjk
'tjk - символы Леви-Чивита, которые определяются:
СЛЧ = 0, если среди r,s,t есть одинаковые
=+1, если индексы r,s,t - различные ® 123, 231, 312
= -1, если этот порядок нарушается
'rst = er × (es ´ et)
wtk характеризует поворот орта t относительно орта k.
Введем тензор второго ранга 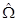 = wtk et ek - тензор поворота
= wtk et ek - тензор поворота
w11 = 0; w12 = u1j '1j2 = - u13; w13 = u1j '1j3 = u12
w21 = u2j '2j1 = u23; w22 = 0; w23 = - u21
w31 = u3j '3j1 = - u32; w32 = u3j '3j2 = u31;
w33 = 0;
Определим компоненты градиента вектора перемещений в специальной системе координат:
( 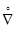 = es (…),s / Hs; Hi = Ai (1 + a3ki) i = 1,2 H3 = 1
= es (…),s / Hs; Hi = Ai (1 + a3ki) i = 1,2 H3 = 1
“o” - в дальнейшем опускаем
Ñu = es (u1e1 + u2e2 + u3e3),s / Hs = e1 (u1,1/H1) e1 + e1 (e1,1 /H1) u1 + e2 (u1,2/H2) e1 +
+ e2 (e1,2 /H2 ) u1 + e3 (u1,3/H3) e1 + e3 (e1,3 /H3) u1 + e1 (u2,1/H1) e2 + e1 (e2,1 /H1) u2 +
+ e2 (u2,2/H2) e2 + e2 (e2,2 /H2) u2 + e3 (u2,3/H3) e2 + e3 (e2,3 /H3) u2 + e1 (u3,1/H1) e3 +
+ e1 (e3,1 /H1) u3 + e2 (u3,2/H2) e3 + e2 (e3,2 /H2) u3 + e3 (u3,3/H3) e3
После подстановки выражений ek,j (j,k = 1,2,3)
Hi = Ai (1 + a3ki) i = 1,2; H3 = 1
h/2 £ a3 £ h/2; учитывая, что h/Ri " 1, т.е. оболочка тонкая, получим:
u11 = u1,1/A1 + (A1,2 / (A1A2)) u2 + u3k1
u12 = u2,1/A1 - (A1,2 / (A1A2)) u1
u13 = u3,1/A1 - u1k1
u21 = u1,2/A2 - (A2,1 / (A1A2)) u2
u22 = u2,2/A2 + (A2,1 / (A1A2)) u1 + u3k2
u23 = u3,2/A2 - u2k2
u31 = u1,3 u32 = u2,3 u33 = u3,3
 = 0,5 (Ñu + ÑuT) Þ eii = uii
= 0,5 (Ñu + ÑuT) Þ eii = uii
Для удлинений имеем:
e11 = u11; e22 = u22; e33 = u33;
Для деформаций сдвига соответственно:
e12 = 0,5 (u12 + u21) = 0,5 [ (A2/A1) (u2/A2),1 + (A1/A2) (u1/A1),2]
e13 = 0,5 (u13 + u31) = 0,5 (u3,1/A1 + u1,3 - u1k1)
e23 = 0,5 (u23 + u32) = 0,5 (u3,2/A2 + u2,3 - u2k2)
Углы поворота определяются через перемещения следующим образом: wii = 0
w12 = - u13 = - u3,1/A1 + u1k1
w21 = u23 = u3,2/A2 - u2k2; w13 = u12
w23 = - u21 w31 = - u32 = - u2,3; w32 = u31 = u1,3.
Дата: 2019-05-29, просмотров: 292.