Рассмотрим произвольную гладкую поверхность и систему декартовых координат x, y, z.

Пусть r = r (a₁, a₂) - радиус-вектор произвольной точки срединной поверхности оболочки. Рассмотрим производные r по переменным a₁ и a₂

r_,1 = r_1; r_,2 = r₂

Введем в рассмотрение базис

r₁ /½r₁½= e₁ r₂ /½r₂½= e₂

и обозначим ½r_a½ = A_a на срединной поверхности S ( a₃ =0). В этом случае r_i = A_i e_i

Составим скалярные произведения:

r_a × r_b =G_ab; G₁₁ = ; G₂₂ =

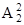
G₁₂ = G₂₁ = 0 для ортогональной системы координат

При этом образуется тензор второго ранга 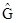= G_ab r_a r_b, который называется первым фундаментальным тензором поверхности.

ds² = (dr) ² = (r_,1 da₁ + r_,2 da₂) ² =

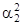= (r₁da₁ + r₂ da₂) ² = G₁₁d  + 2G₁₂ da₁da₂ +C₂₂ d  =

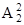= d  + d ;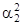

Коэффициенты А₁ и А₂ являются коэффициентами первой квадратичной формы и называются параметрами Ляме. Первая квадратичная форма определяет так называемую внутреннюю геометрию поверхности и определяет метрику поверхности. Введем в рассмотрение единичный вектор внешней нормали к поверхности N. Запишем очевидное соотношение N × N =1 и продифференцируем его по a₁, a₂:

2N × N_{, i} = 0; очевидно, вектор N_{, I} лежит в касательной плоскости к поверхности S и может быть представлен в виде разложения N_{, i} = B_ij r_j.

При этом вводится в рассмотрение тензор второго ранга

= B_ab × r_a × r_b,

являющийся вторым фундаментальным тензором поверхности, а его компоненты B_{ab -} коэффициентами второй квадратичной формы поверхности, определяющей внешнюю геометрию поверхности.

В главных осях тензор может быть записан в виде:

= = k₁e₁e₁ + k₂e₂e₂

k₁ = 1/R₁; k₂ = 1/R₂ –

главные кривизны

В дальнейшем координатные линии выбираются вдоль главных осей кривизны. Пусть в дальнейшем

I₁ = k₁ + k₂ - первый инвариант (средняя кривизна)

I₂ = k₁ × k₂ - второй инвариант (гауссова кривизна)

Специальная система координат в теории оболочек

N = e₁ ´ e₂

Для любой точки тела оболочки:

r (a₁,a₂,a₃) = r (a₁,a₂) + a₃N

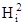 = (r_{, i}) ² = (r_{, i} + (a₃N), i) ² = (r_i + a₃B_ij r_j) ² (B₁₂ = B₂₁ =0)

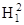= (r₁ + a₃ N_,1) ² = (r₁ + a₃ × B₁₁ r₁) ² =  (1 + a₃k₁) ²

H₁ = A₁ (1 + a₃k₁); H₂ = A₂ (1 + a₃k₂); (½r_i½= A_i)

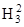 = N × N = 1 ® H₃ = 1 –

параметры Ляме в специальной системе координат

Соотношения Гаусса и Кодацци

Уравнения совместности параметров Ляме:

(H_2,1/H₁),₁ + (H_1,2/H₂),₂ + (H_1,3× H_2,3) / 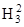= 0

(H_1,2 × H_2,3) / (H₂H₃) - (H_1,3/H₃),₂ = 0

В специальной системе координат

H_b = A_b (1 + a₃k_b); H₃ = 1 (b = 1,2)

Рассмотрим срединную поверхность a₃ = 0

(A_2,1/A₁),₁ + (A_1,2/A₂),₂ + k₁A₁ k₂A₂ = 0 –

соотношение Гаусса.

A_1,2 k₂ - (A₁k₁),₂ = 0, (A₁k₁),₂ = A_1,2 k₂

при замене индексов получаем два соотношения Кодацци

(A₂k₂),₁ = A_2,1 k₁

Вектор перемещений

u = R - r = u₁e₁ + u₂e₂ + u₃e₃

R - текущая конфигурация

r - отсчетная конфигурация

u_{, i} = (u_ke_k), i = (u_k), i e_k + u_k (e_k), i

Дифференцирование ортов в специальной системе координат

e_1,1 = - e₂ (H_1,2/H₂) - e₃ (H_1,3/H₃) = - e₂ 1/ (A₂ (1 + a₃k₂)) × [A₁ (1 + a₃k₁)],₂ -

e₃ × [A₁ (1 + a₃k₁)],₃ = - e₂ 1/ (A₂ (1 + a₃k₂)) [A_1,2 + a₃ (A₁k₁),₂] - e₃ A₁k₁ =

= - e_{2 (}A_1,2 (1 + a₃k₂)) / (A₂ (1 + a₃k₂)) - e₃ A₁k₁ =

= - e₂ (A_1,2/A₂) - e₃ A₁k₁;

e_1,2 = e₂ (H_2,1/H₁) = e₂ 1/ (A₁ (1 + a₃k₁)) [A_2,1 + a₃ (A₂k₂),₁] =

= e_{2 (}A_2,1 (1 + a₃k₁)) / (A₁ (1 + a₃k₁)) = e₂ (A_2,1/A₁);

e_1,3 = e_{3 (}H_3,1/H₁) = 0 (т.к H₃ = 1)

e_2,1 = e₁ (A_1,2/A₂) - получаем из e_1,2 заменой (1«2)

e_2,3 = e_{3 (}H_3,2/H₂) = 0 e_3,2 = e_{2 (}H_2,3/H₃) = e₂ A₂k₂

e_3,1 = e_{1 (}H_1,3/H₃) = e₁ A₁k₁ e_3,3 = 0 (H₃ = 1)