Список обозначений
a1, a2 - криволинейные ортогональные координаты срединной поверхности So оболочки на линиях главных кривизн; для оболочки вращения a1 ─ продольная, a2-окружная координаты; z ─ координата по нормали 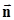 к S;
к S;
А1, А2 -коэффициенты Лямэ; k1, k2 -главные кривизны;
U, V, W - компоненты вектора перемещений произвольной точки оболочки;
u, v, w - компоненты вектора перемещений точек поверхности So;
q 1, q2 - углы поворота нормали 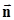 ;
;
ejk - компоненты тензора деформаций;
E11, E22, E12 - компоненты тангенциальной деформации на S: растяжения-сжатия по направлениям координат a1 и a2 и сдвиг;
K11, K22, K12 - компоненты изгибной деформации: изменения главных кривизн и кручение;
T11, T22, S - тангенциальные внутренние усилия, приведенные к So: усилия растяжения-сжатия и сдвига;
M11, M22, H - изгибающие и крутящий моменты;
Q11, Q22 - перерезывающие силы;
q1, q2, q3 - компоненты внешней поверхностной нагрузки, приведенные к S;
E, n - модуль Юнга и коэффициенты Пуассона материала оболочки;
yj -унифицированные обозначения основных независимых переменных в разрешающих системах обыкновенных дифференциальных уравнений (ОДУ);
fj - операторы правых частей канонических систем ОДУ;
Рассмотрим элемент произвольной тонкой оболочки, пусть в дальнейшем
h - толщина оболочки, принимаемая в дальнейшем постоянной.
Обозначим через R1, R2- главные радиусы кривизны срединной поверхности оболочки S. R=min {R1, R2}.
Основным геометрическим параметром оболочки является параметр тонкостенности или относительная толщина, определяемый отношением e=h/R.
Принята достаточно условная классификация оболочек по ее толщине на тонкие, средней длины и толстые оболочки.
Будем считать оболочку тонкой, если ее относительная толщина значительно меньше единицы. Обычно оболочки считают тонкими при значении e<1/20. Значения 1/20 < e < 1/10 соответствуют оболочке средней толщины, а e > 1/10 - толстой оболочке.
Для незамкнутых оболочек можно задать характерный размер размер a. Тогда параметр тонкостенности можно определить как e = min (h/a, h/R).
Поверхность оболочки S, равноотстоящая от лицевых поверхностей S+ и S - называется ее срединной поверхностью.
Специальная система координат в теории оболочек
N = e1 ´ e2
Для любой точки тела оболочки:
r (a1,a2,a3) = r (a1,a2) + a3N
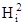 = (r, i) 2 = (r, i + (a3N), i) 2 = (ri + a3Bij rj) 2 (B12 = B21 =0)
= (r, i) 2 = (r, i + (a3N), i) 2 = (ri + a3Bij rj) 2 (B12 = B21 =0)
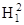 = (r1 + a3 N,1) 2 = (r1 + a3 × B11 r1) 2 =
= (r1 + a3 N,1) 2 = (r1 + a3 × B11 r1) 2 =  (1 + a3k1) 2
(1 + a3k1) 2
H1 = A1 (1 + a3k1); H2 = A2 (1 + a3k2); (½ri½= Ai)
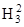 = N × N = 1 ® H3 = 1 –
= N × N = 1 ® H3 = 1 –
параметры Ляме в специальной системе координат
Деформации сдвига
Выделим два прямолинейных волокна, направление которых определяется единичными векторами m1 и m2
dr1 = m1ds1; dr2 = m2ds2;
dsi = ½dri½ - длины элементов волокон до деформаций
Деформации сдвига характеризуется изменением угла q12
cos q12 - cos Q12 = (dr1× dr2) / (ds1× ds2) - (dR1× dR2) / (dS1× dS2) =
= m1 × m2 - [ (dr1× 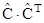 × dr2) / ds1 (1+em1) ds2 (1+em2)] =
× dr2) / ds1 (1+em1) ds2 (1+em2)] =
= m1 × m2 - m1× 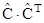 × m2 = m1× (
× m2 = m1× ( 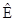 -
- 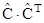 ) × m2 = - 2m1×
) × m2 = - 2m1× 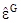 × m2;
× m2;
Пусть m1 = e1; m2 = e2; m1 × m2 = 0
cos q12 = 0 0 - cos Q12 = -2 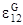
cos Q12 = cos (p/2 - g12) = 2 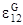 = sin g12 = g12
= sin g12 = g12
g12 - угол сдвига; g12 » e12, если g12 - небольшой
Повороты
Рассмотрим материальное волокно dr = e ds
w = (dr ´ dR) / (½dr½×½dR½) - вектор поворота материального волокна
½w½= sin j
w - нормаль, относительно которой происходит поворот
w = (dr ´ (dr × 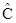 )) / (ds×ds (1 + ee)) = e ´ (e×
)) / (ds×ds (1 + ee)) = e ´ (e× 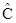 ) =
) =
= e ´ [e × ( 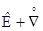 u)] = e ´ e + e ´ (e ×
u)] = e ´ e + e ´ (e × 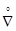 u) = e ´ (e ×
u) = e ´ (e × 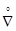 u)
u)
Пусть e = et - базисные вектора t = 1,2,3
wt - вектор поворота материального волокна t
wt = et ´ (et × 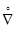 u) = et ´ (et × ukj ek ej) =
u) = et ´ (et × ukj ek ej) =
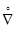 u = ukj ek ej
u = ukj ek ej  = et ´ (ukj dtk ej) = et ´ utj ej =
= et ´ (ukj dtk ej) = et ´ utj ej =
= utj 'tjk ek = wtk ek = wt, где wtk = utj 'tjk
'tjk - символы Леви-Чивита, которые определяются:
СЛЧ = 0, если среди r,s,t есть одинаковые
=+1, если индексы r,s,t - различные ® 123, 231, 312
= -1, если этот порядок нарушается
'rst = er × (es ´ et)
wtk характеризует поворот орта t относительно орта k.
Введем тензор второго ранга 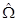 = wtk et ek - тензор поворота
= wtk et ek - тензор поворота
w11 = 0; w12 = u1j '1j2 = - u13; w13 = u1j '1j3 = u12
w21 = u2j '2j1 = u23; w22 = 0; w23 = - u21
w31 = u3j '3j1 = - u32; w32 = u3j '3j2 = u31;
w33 = 0;
Определим компоненты градиента вектора перемещений в специальной системе координат:
( 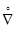 = es (…),s / Hs; Hi = Ai (1 + a3ki) i = 1,2 H3 = 1
= es (…),s / Hs; Hi = Ai (1 + a3ki) i = 1,2 H3 = 1
“o” - в дальнейшем опускаем
Ñu = es (u1e1 + u2e2 + u3e3),s / Hs = e1 (u1,1/H1) e1 + e1 (e1,1 /H1) u1 + e2 (u1,2/H2) e1 +
+ e2 (e1,2 /H2 ) u1 + e3 (u1,3/H3) e1 + e3 (e1,3 /H3) u1 + e1 (u2,1/H1) e2 + e1 (e2,1 /H1) u2 +
+ e2 (u2,2/H2) e2 + e2 (e2,2 /H2) u2 + e3 (u2,3/H3) e2 + e3 (e2,3 /H3) u2 + e1 (u3,1/H1) e3 +
+ e1 (e3,1 /H1) u3 + e2 (u3,2/H2) e3 + e2 (e3,2 /H2) u3 + e3 (u3,3/H3) e3
После подстановки выражений ek,j (j,k = 1,2,3)
Hi = Ai (1 + a3ki) i = 1,2; H3 = 1
h/2 £ a3 £ h/2; учитывая, что h/Ri " 1, т.е. оболочка тонкая, получим:
u11 = u1,1/A1 + (A1,2 / (A1A2)) u2 + u3k1
u12 = u2,1/A1 - (A1,2 / (A1A2)) u1
u13 = u3,1/A1 - u1k1
u21 = u1,2/A2 - (A2,1 / (A1A2)) u2
u22 = u2,2/A2 + (A2,1 / (A1A2)) u1 + u3k2
u23 = u3,2/A2 - u2k2
u31 = u1,3 u32 = u2,3 u33 = u3,3
 = 0,5 (Ñu + ÑuT) Þ eii = uii
= 0,5 (Ñu + ÑuT) Þ eii = uii
Для удлинений имеем:
e11 = u11; e22 = u22; e33 = u33;
Для деформаций сдвига соответственно:
e12 = 0,5 (u12 + u21) = 0,5 [ (A2/A1) (u2/A2),1 + (A1/A2) (u1/A1),2]
e13 = 0,5 (u13 + u31) = 0,5 (u3,1/A1 + u1,3 - u1k1)
e23 = 0,5 (u23 + u32) = 0,5 (u3,2/A2 + u2,3 - u2k2)
Углы поворота определяются через перемещения следующим образом: wii = 0
w12 = - u13 = - u3,1/A1 + u1k1
w21 = u23 = u3,2/A2 - u2k2; w13 = u12
w23 = - u21 w31 = - u32 = - u2,3; w32 = u31 = u1,3.
Гипотезы Кирхгофа-Лява
Результаты, полученные в предыдущих параграфах, основаны на геометрических и статических соображениях. Однако их недостаточно для полного построения теории оболочек. При выборе соотношений, связывающих компоненты деформаций с перемещениями и усилия и моменты с компонентами деформаций приходится принимать некоторые упрощающие подходы. Первый заключается в том, что оболочку рассматривают как трехмерное упругое тело. Решение соответствующих уравнений теории упругости разыскиваются путем разложения всех величин в ряды по степеням точки оболочки от срединной поверхности. Этот подход, предложенный в теории пластин А. Коши, позволяет при удержании достаточного числа членов (при условии сходимости рядов) получить решение близкое к точному. Этот метод весьма громоздок, поэтому в большинстве случаев идут по другому пути. Во втором подходе предложенном также при построении теории пластин Г. Кирхгоффом принимаются гипотезы, аналогичные тем, которые используются в теории балок:
прямолинейные и нормальные к срединной поверхности волокна недеформированной оболочки остаются прямолинейными и нормальными к деформированной срединной поверхности и не меняют своей длины;
нормальные напряжения на площадках, параллельных площадкам срединной поверхности, пренебрежимо малы по сравнению с другими напряжениями.
Первая гипотеза имеет геометрический характер, вторая - статический. Теория оболочек, основанная на гипотезах Кирхгоффа, была построена, в основном А. Лявом, поэтому в теории оболочек гипотезы 1 и 2 принято называть гипотезами Кирхгоффа-Лява. Иногда их называют гипотезой жесткой (недеформированной) нормали или гипотезой сохранения нормали.
Гипотеза 1 используется только для записи зависимостей деформации оболочки от перемещений, гипотеза 2 - для записи зависимостей деформаций от напряжений. В первом случае предполагается, что в нормальных сечениях отсутствуют сдвиги e13 = e23 = 0, и поперечные деформации e33 = 0. Во втором случае допускается, что нормальное напряжение s33 незначительно влияет на деформации e11 и e22, так что эти деформации выражаются через нормальные напряжения s11, s22 и s33 << {s11, s12, s22}. Таким образом гипотезу 1 нельзя понимать в буквальном смысле, поскольку в действительности в оболочках имеют место поперечные сдвиги - поперечные или как их иногда называют перерезывающие силы не равны нулю.
Гипотезы Кирхгоффа-Лява просты и физичны. Они позволяют свести трехмерную задачу определения напряженно-деформированного состояния оболочки к двумерной. Исследование поведения элемента оболочки в рамках этих гипотез сводится к исследованию поведения ее срединной поверхности. Следует отметить, что теория, построенная на гипотезах Кирхгоффа-Лява, является существенно приближенной. Принятие этих гипотез вносит погрешность порядка h/R, где h - толщина оболочки, R - минимальный линейный размер срединной поверхности.
Рассмотрим элемент тонкой оболочки со срединной поверхностью S. До деформирования в исходной конфигурации радиус-вектор произвольной точки оболочки, не лежащей на срединной поверхности может быть представлен в виде:
r (a1, a2, a3) = r (a1, a2) + a3n
r (a1, a2) - радиус-вектор проекции точки на S до деформации.
После деформирования (в актуальной конфигурации)
R (a1, a2, a3) = P (a1, a2) + a3N
P (a1, a2) - радиус-вектор проекции точки на S после деформации
Тогда вектор перемещений запишется в виде:
u = R - r = P - r + a3 (N - n) = = u° (a1, a2) + a3u1 (a1, a2)
u° - вектор перемещений точек, лежащих на S
В координатной форме соответственно:
u1 = 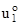 (a1, a2) + a3
(a1, a2) + a3  (a1, a2)
(a1, a2)
u2 = 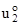 (a1, a2) + a3
(a1, a2) + a3 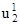 (a1, a2)
(a1, a2)
u3 = 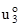 (a1, a2)
(a1, a2)
При этом компоненты вектора перемещений u1 и u2 линейным образом зависят от координаты a3, а функция поперечного прогиба постоянна по толщине в силу недеформируемости нормали.
Рассмотрим детальнее геометрическую гипотезу Кирхгоффа-Лява. Тот факт, что нормаль к срединной поверхности S в процессе деформирования остается нормалью приводит к соотношениям:
e13 = 0, e23 = 0
Таким образом
u3,1/A1 + u1,3 - u1k1 = 0
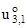 /A1 +
/A1 +  - (
- (  + a3
+ a3  ) k1 = 0
) k1 = 0
 (1 - a3k1) -
(1 - a3k1) -  k1 +
k1 + 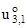 /A1 = 0
/A1 = 0
считая оболочку достаточно тонкой, пренебрегаем членом a3k1 << 1
 (a1, a2) = -
(a1, a2) = - 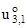 /A1 +
/A1 +  k1
k1

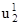 (a1, a2) = -
(a1, a2) = - 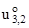 /A2 +
/A2 + 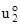 k2
k2
w12 = - u3,1/A1 + u1k1 = - 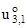 /A1 +
/A1 +  k1 + a3k1
k1 + a3k1  =
=
= - 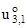 /A1 +
/A1 +  k1 + a3k1 (-
k1 + a3k1 (- 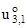 /A1 +
/A1 +  k1) =
k1) =
= (- 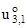 /A1 +
/A1 +  k1) (1 + a3k1) =
k1) (1 + a3k1) =  (1 + a3k1) »
(1 + a3k1) »  =
=
= - 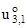 /A1 +
/A1 +  k1 = q1 (a1, a2) - угол поворота на поверхности S.
k1 = q1 (a1, a2) - угол поворота на поверхности S.
Аналогично:
w21 = u3,2/A2 - u2k2 »  =
= 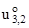 /A2 -
/A2 - 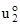 k2 = -
k2 = - 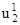 = - q2 (a1, a2)
= - q2 (a1, a2)
Обозначим: 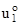 = u;
= u; 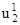 = v;
= v; 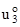 = w тогда можно записать:
= w тогда можно записать:
u1 = u + a3q1, u2 = v + a3q2, u3 = w
Введем в рассмотрение плоский вектор перемещений и поворотов:
u = ue1 + ve2
q = q1e1 + q2e2
Тензор кривизны в главных осях можно представить в виде:
 = k1e1e1 + k2e2e2; ki = 1/Ri
= k1e1e1 + k2e2e2; ki = 1/Ri
Окончательно кинематические соотношения, соответствующие теории Кирхгоффа-Лява запишутся в виде:
q = -Ñw + 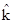 × u Ñ = es (1/As) (¶/¶s) (s = 1,2)
× u Ñ = es (1/As) (¶/¶s) (s = 1,2)
u (a1, a2, a3) = u1e1 + u2e2 = u (a1, a2) + a3q (a1, a2)
u3 = w (a1, a2)
С учетом проведенных выкладок для компонентов тензора деформаций имеем:
e11 = e11 + 0,5  =
= 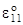 + a3
+ a3 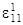
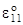 =
=  /A1 + A1,1 / (A1A2)
/A1 + A1,1 / (A1A2) 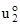 +
+  k1 + 0,5
k1 + 0,5 
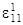 = q1,1/A1 + A1,1 / (A1A2) q2 (w12 = q1)
= q1,1/A1 + A1,1 / (A1A2) q2 (w12 = q1)
e22 = e22 + 0,5 
 =
=  /A2 + A2,1 / (A1A2)
/A2 + A2,1 / (A1A2) 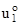 +
+ 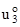 k2 + 0,5
k2 + 0,5 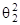
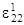 = q2,2/A2 + A2,1 / (A1A2) q1
= q2,2/A2 + A2,1 / (A1A2) q1
e12= e12 - 0,5w12w21 = e12 + 0,5q1q2 = 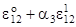 (w21 = -q2)
(w21 = -q2)
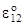 = 0,5 [ (A2/A1) (
= 0,5 [ (A2/A1) ( 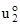 /A2),1 + (A1/A2) (
/A2),1 + (A1/A2) ( 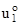 /A1),2] + 0,5q1q2
/A1),2] + 0,5q1q2
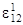 = 0,5 [ (A2/A1) (q2 /A2),1 + (A1/A2) (q1/A1),2]
= 0,5 [ (A2/A1) (q2 /A2),1 + (A1/A2) (q1/A1),2]
Введем в рассмотрение плоский тензор деформаций
 = e11e1e1 + e12 (e1e2 + e2e1) + e22e2e2
= e11e1e1 + e12 (e1e2 + e2e1) + e22e2e2
Он может быть записан в другой форме:
 =
= 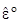 + a3
+ a3  , где
, где
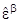 =
=  e1e1 +
e1e1 + 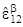 (e1e2 + e2e1) +
(e1e2 + e2e1) + 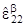 e2e2 (b = 0,1)
e2e2 (b = 0,1)
Таким образом использование геометрической гипотезы Кирхгоффа-Лява приводит к линейному распределению перемещений и деформаций по толщине оболочки. В компактной форме можно записать:
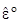 = 0,5 (Ñu+ ÑuT) +
= 0,5 (Ñu+ ÑuT) + 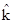 w + 0,5qq
w + 0,5qq
 = 0,5 (Ñq + ÑqT)
= 0,5 (Ñq + ÑqT)
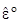 характеризует деформации растяжения-сжатия срединной поверхности S,
характеризует деформации растяжения-сжатия срединной поверхности S, 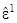 - изменение кривизн и кручение срединной поверхности.
- изменение кривизн и кручение срединной поверхности.
Список обозначений
a1, a2 - криволинейные ортогональные координаты срединной поверхности So оболочки на линиях главных кривизн; для оболочки вращения a1 ─ продольная, a2-окружная координаты; z ─ координата по нормали 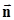 к S;
к S;
А1, А2 -коэффициенты Лямэ; k1, k2 -главные кривизны;
U, V, W - компоненты вектора перемещений произвольной точки оболочки;
u, v, w - компоненты вектора перемещений точек поверхности So;
q 1, q2 - углы поворота нормали 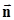 ;
;
ejk - компоненты тензора деформаций;
E11, E22, E12 - компоненты тангенциальной деформации на S: растяжения-сжатия по направлениям координат a1 и a2 и сдвиг;
K11, K22, K12 - компоненты изгибной деформации: изменения главных кривизн и кручение;
T11, T22, S - тангенциальные внутренние усилия, приведенные к So: усилия растяжения-сжатия и сдвига;
M11, M22, H - изгибающие и крутящий моменты;
Q11, Q22 - перерезывающие силы;
q1, q2, q3 - компоненты внешней поверхностной нагрузки, приведенные к S;
E, n - модуль Юнга и коэффициенты Пуассона материала оболочки;
yj -унифицированные обозначения основных независимых переменных в разрешающих системах обыкновенных дифференциальных уравнений (ОДУ);
fj - операторы правых частей канонических систем ОДУ;
Рассмотрим элемент произвольной тонкой оболочки, пусть в дальнейшем
h - толщина оболочки, принимаемая в дальнейшем постоянной.
Обозначим через R1, R2- главные радиусы кривизны срединной поверхности оболочки S. R=min {R1, R2}.
Основным геометрическим параметром оболочки является параметр тонкостенности или относительная толщина, определяемый отношением e=h/R.
Принята достаточно условная классификация оболочек по ее толщине на тонкие, средней длины и толстые оболочки.
Будем считать оболочку тонкой, если ее относительная толщина значительно меньше единицы. Обычно оболочки считают тонкими при значении e<1/20. Значения 1/20 < e < 1/10 соответствуют оболочке средней толщины, а e > 1/10 - толстой оболочке.
Для незамкнутых оболочек можно задать характерный размер размер a. Тогда параметр тонкостенности можно определить как e = min (h/a, h/R).
Поверхность оболочки S, равноотстоящая от лицевых поверхностей S+ и S - называется ее срединной поверхностью.
Криволинейные, ортогональные системы координат
Правило дифференцирования базисных векторов криволинейной ортогональной системы координат определяется следующим образом:
es,t = - (Ht,s /Hs) et - dstÑHt
Ñ = em (…),m / Hm
Здесь Hm - параметры Ляме координатной системы, имеющие вид
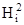 = (r, i) 2; Hi = ½ r, i ½ .
= (r, i) 2; Hi = ½ r, i ½ .
Здесь r, I - радиус - вектор произвольной точки тела оболочки. В частности:
e1,1 = (H1,1/H1) e1 - (H1,1/H1) e1 - (H1,2/H2) e2 - (H1,3/H3) e3
e1,2 = (H2,1/H1) e2; e3,2 = (H2,3/H3) e2; Hi (a1, a2, a3)
Запишем условие совместности, которое в принятых обозначениях имеет вид:
(e1,1),2 = (e1,2),1
(e1,2),1 = ( (H2,1/H1) e2),1 = (H2,1/H1),1 e2 + (H2,1/H1) (H1,2/H2) e1;
(e1,1),2 = - [ (H1,2/H2) e2 + (H1,3/H3) e3],2 =
= - (H1,2/H2),2 e2 + (H1,2/H2) ( (H2,1/H1) e1+ (H2,3/H3) e3) -
(H1,3/H3),2 e3 - (H1,3/H3) (H2,3/H3) e2
Тогда, приравнивая коэффициенты при базисных векторах, получим:
e1: (H2,1H1,2) / (H1H2) - (H2,1H1,2) / (H1H2) º 0 - тождество
e2: (H2,1/H1),1 + (H1,2/H2),2 + (H1,3 × H2,3) / 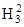 = 0
= 0
e3: (H1,2 × H2,3) / (H2H3) - (H1,3/H3),2 = 0
Круговая перестановка индексов приводит к шести уравнениям совместности параметров Ляме.
Дата: 2019-05-29, просмотров: 283.