!!! Схему Горнера и вычисление на калькуляторе можно применить и для перевода дробных чисел. Например:
0.11012 = 1 * 2-1 + 1 * 2-2 + 0 * 2-3 + 1 * 2-4 = 1 * 2-4 + 0 * 2-3 + 1 * 2-2 + 1 * 2-1 = (((1/2 + 0)/2 + 1)/2 +1)/2 = 0.812510.
| 1 | / | 2 | + | 0 | / | 2 | + | 1 | / | 2 | + | 1 | / | 2 | = |
Прибавление нулей можно не делать, тогда число операций сложения сократится:
| 1 | / | 2 | / | 2 | + | 1 | / | 2 | + | 1 | / | 2 | = |
Перевод целого двоичного числа в 16-ричную систему проводится путем разбиения числа на тетрады (группы по 4 цифры):
1 1000 1101 1001 2 = 18 D 9 16
Перевод целого двоичного числа в 8-ричную систему проводится путем разбиения числа на триады (группы по 3 цифры):
1 100 011 011 001 2 = 14331 8
Для перевода дробных частей двоичных чисел в 8-ричную или 16-ричную системы аналогичное разбиение (на триады или тетрады) проводится вправо от запятой (с дополнением недостающих последних цифр нулями):
0,1100011101 2 = 0,110001110100 2 = 0,61648
0,1100011101 2 = 0,110001110100 2 = 0,С7416
Перевод 8-ричных (16-ричных) чисел в 2-ичные проводится сопоставлением каждому знаку числа соответствующей тройки (четверки) двоичных цифр.
Таблицы сложения и умножения в 2-ичной системе:
| + | 0 | 1 | * | 0 | 1 | |
| 0 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 10 | 1 | 0 | 1 |
Двоичное умножение выполняется по тем же правилам, что и десятичное и сводится к сдвигам множимого и суммированию.
Арифметические действия с числами в 2-ичной, 8-ричной и
16-ричной системах счисления выполняются по аналогии с 10-ичной:
| 11101111 2 + 12 11110000 2 | 67 8 +5 8 74 8 | AB 16 +A 16 B 5 16 |
Формы представления чисел
Представление чисел в памяти компьютера имеет некоторые особенности:
· ограниченная разрядная сетка компьютера приводит к ограничению диапазона представимых чисел;
· при выполнении операций умножения и сложения возможен выход за пределы разрядной сетки, так называемое переполнение.
Представление целых чисел
Целые числа при хранении в памяти могут занимать 1 байт, 2 байта, 4 байта. Наименьшее по абсолютной величине число, хранимое в ячейке памяти, равно нулю. Самое большое положительное число имеет такое представление (например, в однобайтовом представлении): 011111112 = 7F16. В 10-ичной с/с это число равно
27-1=127.
Если размер ячейки N битов, то максимальное целое положительное число, хранимое в ячейке, равно 2N-1-1.
Логическое представление целых положительных чисел:
· Исходное целое число переводится в 16-ичную систему счисления (чтобы сократить количество операций деления).
· Полученное число из 16-ричной системы счисления переводится в 2-ичную систему счисления (каждый 16-ричный знак заменяется соответствующей ему тетрадой двоичных чисел).
· Записываем двоичное представление числа:
· Последовательно в битах справа налево записывается полученное двоичное представление числа.
· В крайнем слева бите записывается знак числа – в данном случае 0.
В оперативной памяти компьютера полученное представление числа располагается в перевернутом виде (от младшего байта к старшему).
Например:
25610 = ?2
25610 = 010016 = 00000001000000002
| Логическое представление | старший байт (с большим номером) | младший байт (с меньшим номером) | ||||||||||||||
| Номер разряда | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Значение разряда | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
 |
В памяти это число хранится в виде: 000116
А как хранить отрицательные числа? Пусть имеем 4 бита памяти компьютера, выделяем один бит для хранения знака числа. Тогда, например, - 5 будет храниться как 1101, а 5 – как 0101. Диапазон представления чисел в этом случае будет уже не от 0 до 15, а от - 7 до 7, т. е. 15 различных значений (в 4 битах есть возможность хранить 16 различных последовательностей). Последовательность 1000 не задействована или, что еще более неприятно, она может трактоваться как - 0 , а это уже из разряда необъяснимых фактов, 0 и - 0.
Выполним инверсию и прибавление 1 к двоичному числу:
| Число | Двоичное представление | Инверсия | Прибавление 1 | Отрицательное число |
| 1 | 0001 | 1110 | 1111 | -1 |
| 2 | 0010 | 1101 | 1110 | -2 |
| 3 | 0011 | 1100 | 1101 | -3 |
| 4 | 0100 | 1011 | 1100 | -4 |
| 5 | 0101 | 1010 | 1011 | -5 |
| 6 | 0110 | 1001 | 1010 | -6 |
| 7 | 0111 | 1000 | 1001 | -7 |
| 8 | 1000 | 0111 | 1000 | -8 |
| 0 | 0000 | 1111 | 10000 | 0 |
В предпоследнем столбце мы получаем двоичное представление отрицательных чисел. Все 16 двоичных последовательностей задействованы, диапазон представления от -8 до 7 и представление 0 однозначно. Представление отрицательных чисел в том виде, который приведен в таблице, называется дополнительным кодом. Представление положительных чисел в дополнительном коде совпадает с их обычным представлением.
Смысл понятия «дополнительный код» можно объяснить так: если Х – есть положительное целое число, представленное в N разрядах, а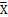 
– его дополнительный код, то справедливо:
Арифметическое устройство компьютера не умеет выполнять операцию вычитания. Вычитание сводится к сложению первого слагаемого с дополнительным кодом второго слагаемого. Это – конструкторская хитрость, позволяющая оптимизировать устройство процессора.
Максимальное по абсолютной величине целое отрицательное число, хранимое в ячейке памяти (например, в однобайтовом представлении), равно 100000002 = 8016. В 10-ичной с/с это число равно -27=-128.
Если размер ячейки N битов, то максимальное по абсолютной величине целое отрицательное число, хранимое в ячейке, равно -2N-1.
Логическое представление отрицательных целых чисел (представление в дополнительном двоичном коде):
· Исходное число рассматривается как положительное и переводится в 16-ричную систему счисления.
· Полученное число из 16-ричной системы счисления переводится в 2-ичную систему счисления.
· Полученное представление числа инвертируется (нули заменяются единицами, а единицы – нулями).
· К полученному представлению добавляется 1 в самый младший разряд.
· Записываем двоичное представление числа:
· Последовательно в битах справа налево записывается полученное двоичное представление числа.
· В крайнем слева бите записывается знак числа – в данном случае 1.
В оперативной памяти компьютера полученное представление числа располагается в перевернутом виде (от младшего байта к старшему).
Например:
-25610 = ?2
25610 = 010016 =1000000002 = 0000000100000000
0111111011111111
+ 1
0111111100000000
Самый левый бит устанавливаем в 1, так как число отрицательное. Тогда имеем:
| Логическое представление | Старший байт | Младший байт | ||||||||||||||
| Номер разряда | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Значение разряда | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Логическое представление (в 16-ричной системе): FF 00 , в памяти – 00 FF .
Особенности целочисленной машинной арифметики:
- преимущества (по сравнению с арифметикой вещественных чисел)
o целые числа всегда представимы своими точными значениями
o операции целочисленной арифметики всегда дают точные результаты
o операции целочисленной арифметики всегда выполняются быстрее, чем операции вещественной арифметики
· недостатки
o сравнительно узкий диапазон допустимых значений (для каждого типа свой)
o при выполнении программы автоматически не контролируется выход за этот диапазон (эффект переполнения), не происходит прерывания работы процессора и просто получается неверный результат.
o если есть опасность переполнения, то программист в программе должен сам предусматривать предупреждение этого.
Дата: 2019-05-28, просмотров: 195.
