Представление информации в компьютере

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лекция 3

Представление информации в компьютере

Ищу ответы на свои вопросы,А если не на все, хоть на один,Но здесь значения не имеют дозы…Желаю знать: Я раб иль господин?

Представление информации в компьютере. 1

Количественная мера информации. 1

Представление текстовой информации. 5

Представление чисел. 8

Перевод чисел из одной системы счисления в другую.. 11

Формы представления чисел. 15

Представление целых чисел. 15

Представление вещественных чисел с плавающей точкой. 18

Представление графической информации. 21

Представление звука. 23

ASCII-Коды (символы с кодами 0-127) 26

Кодовая таблица 866 – MS-DOS. 27

Кодовая таблица 1251 – MS Windows. 28

В результате изучения материала лекции необходимо знать. 29

Программист, используя в программах, выполняемых в консольном режиме, строковые и символьные константы с русскими буквами, сталкивается с проблемой различия кодировок.

Сегодня в большинстве приложений Windows используется универсальный стандарт кодирования символов, представляющий собой 16-битную кодировку символов для всех языков – Unicode (юникод), допускающий 2¹⁶=65536 кодовых комбинаций для практически всех применяемых символов (букв алфавитов разных языков, математических, декоративных символов и т.д.). В отличие от ASCII, в Unicode один символ кодируется двумя байтами.

Коды в стандарте Unicode разделены на несколько областей. Область с кодами от U+0000 до U+007F содержит символы набора ASCI с соответствующими кодами. Символы ASCII включены в Unicode как расширенные. Далее расположены области знаков различных письменностей, знаки пунктуации и технические символы. Часть кодов зарезервирована для использования в будущем.

Представление чисел

Система счисления – способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.

Системы счисления делятся на позиционные и непозиционные.

В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе. Например, в римской системе счисления в качестве цифр используются латинские буквы, записываемые слева направо в порядке убывания:

1 – I , 5 – V , 10 – X , 50 – L , 100 – С, 500 – D , 1000 – M ,
Например:

DDCXXII =1122: два раза по 500, один раз – 100, 2 раза по 10 и две единицы;

MMII =2002: два раза по 1000 и две единицы.

Если же в записи числа справа записана цифра, большая, чем слева, то это означает уменьшение цифры справа на значение цифры слева:

MCMII =1902, т.к. означает M ( CM ) II , т.е. 1000 + 900 +2.

Системы счисления, в которых вклад каждой цифры в величину числа (количественное значение цифры) зависит от ее позиции в последовательности цифр, изображающей число, называются позиционными.

Каждая позиция в записи числа называется разрядом числа.

Например, в 10-ичной системе счисления число
3377₁₀ =3*10³+3*10²+7*10¹+7*10⁰ =3*1000+3*100+7*10+7, т.е. вклад и цифры 3, и цифры 7 различен.

Это же число в 5-ричной системе счисления записывается как 102002₅ , т.к. 3377 = 1*5⁵ +0*5⁴ +2*5³ +0*5² + 0*5¹ +2*5⁰, где 5⁵=3125, а 5³=125.

Это же число в 2-ичной системе счисления записывается как 110100110001₂ , т.к. 3377 = 1*2¹¹ +1*2¹⁰ +0*2⁹ +1*2⁸ +0*2⁷ +0*2⁶ +1*2⁵ +1*2⁴ +0*2³ +0*2² +0*2¹+1*2⁰, где 2 ¹¹ = 2048 , 2¹⁰=1024, 2⁹ = 512, 2⁸ =256 и т. д.

Запись произвольного числа А в позиционной системе счисления:

А = ± а _m-1 a_m-2…a_i…a₁a₀ , a_-1 a_-2…a_-n,

где m – количество целых разрядов; n – дробных; m+n – разрядность числа.

Разряды числа нумеруются:

· в целой части числа положительными целыми числами, начиная с нуля,

· в дробной – отрицательными числами, начиная с -1.

Например, для числа 7137.436 имеем:

разряды	3210-1-2-3
число	7137,4 3 6

Основание позиционной системы – это число, которое:

• определяет количество различных цифр, используемых для представления числа;

• показывает, во сколько раз единица (i -1) разряда числа меньше единицы i-го разряда этого числа.

Наименьшим основанием для позиционных систем является 2.

Развернутой формой записи числа А в позиционной системе счисления с основанием q называется разложение числа в ряд по степеням q, представляющее собой его значение:

А _q = ± а _m-1 q^m-1+…+ a_i qⁱ …+ a₁q¹ + a₀ q⁰ + …+a_-nq^-n ,

А=777.77 при q=10, m =3, n =2 (цифра 7 представляет сотни, десятки, единицы, десятые и сотые доли единицы):

Для числа 123,456 при q=10, m =3, n =3 развернутая форма записи выглядит так:

123.456₁₀ = 1* 10² + 2* 10¹ + 3* 10⁰+ 4* 10^-1 + 5* 10^-2 + 6* 10^-3.

Для числа -101,1101 при q=2, m =3, n =4 развернутая форма записи выглядит так:

-101.1101₂= -(1* 2² + 0* 2¹+ 1* 2⁰+ 1* 2^-1+ 1* 2^-2+ 1* 2^-4).

Для числа AB .1 F 2 при q=16, m =2, n =3:

AB .1 F 2₁₆ = A * 16¹ + B * 16⁰+ 1* 16^-1 + F * 16^-2 + 2*16^-3 =171.12158203₁₀;

Количество различных чисел, которое можно представить в q-ичной системе счисления, зависит от основания системы q и разрядности числа (значений m и n).

Максимальное целое число, которое может быть представлено в m разрядах системы счисления с основанием q:

N_max= q^m–1.

Минимальное значащее (не равное 0) число, которое можно записать в n разрядах дробной части:

N_min = q^-ⁿ.

Вводимые в компьютер числа (и выводимые из него), как правило, представляются в 10-ичной системе счисления. В ЭВМ данные любого типа – числовые, символьные, графические, звуковые – представляются в 2-ичной с/с. Для компактного представления числовые данные записываются в 16-ричной с/с.

Преобразование чисел при вводе в двоичную систему (в которой числа представляются в памяти) и обратно в десятичную, при выводе, выполняется программно.

Диапазоны цифр для представления чисел в различных системах счисления представлены в таблице 2.

Таблица 2. Диапазоны цифр для представления чисел в различных системах счисления

Основание системы счисления	16	10	8	4	3	2
Диапазон цифр	0 - 15	0 - 9	0 - 7	0 - 3	0 - 2	0 - 1

Для представления восьмеричной цифры необходимо 3 двоичных разряда. Если есть 4 бита, то это 16 различных двоичных последовательностей для хранения целых неотрицательных чисел. Итак, мы можем хранить в этом случае числа из интервала от 0 до 15.

В двоично-десятичной системе каждая десятичная цифра также представляется четырьмя двоичными разрядами, но используются не 16, а только 10 значений 4-разрядного двоичного числа.

При работе с битами не так легко выразить любое число, используя только единицы и нули, т.е. его двоичное представление. Для этого используются шестнадцатеричные числа. В 16-ричной системе счисления значения разрядов от 0 до 9 изображаются десятичными цифрами, а значения от 10 до 15 – латинскими буквами A( a), B( b), C( c), D( d), E( e), F( f). Если основание системы превышает 10, то в качестве дополнительных цифр выступают буквы латинского алфавита по порядку.

Значения двоичных кодов десятичных и шестнадцатеричных цифр представлены в таблице 3.

Таблица 3. Значения двоичных кодов десятичных и шестнадцатеричных цифр

цифра	код	цифра	код
0	0000	8	1000
1	0001	9	1001
2	0010	A	1010
3	0011	B	1011
4	0100	C	1100
5	0101	D	1101
6	0110	E	1110
7	0111	F	1111

8 78 16

14 4 1 256₁₀= 4Е8 ₁₆

1256 ₁₀ = 4Е8 ₁₆ = 0000 0100 1110 1000 ₂ = 0000010011101000 ₂

Для перевода целого числа из системы счисления с основанием p в 10-ичную систему счисления используем развернутую форму записи числа в системе счисления с основанием p. Например:

11101₂ = 1*2⁴ + 1*2³ + 1*2² +1*2⁰=29₁₀.

Выполним перевод числа DFF₁₆ в 10-ичную систему:

DFF₁₆ = D*16²+ F*16¹ + F*16⁰ = 13*16² + 15*16¹ + 15*16⁰ = 3583₁₀.

!!! Недесятичное число можно быстро перевести в 10-ичную с/с с помощью калькулятора. Для этого надо применить схему Горнера для вычисления алгебраических многочленов. Например:

231745₈=2*8⁵ + 3*8⁴ + 1*8³ + 7*8² + 4*8¹ +5 =
((((2*8 + 3)*8 + 1)*8 + 7)*8 + 4)*8 + 5 = 78821₁₀

Скобочное выражение можно вычислить на калькуляторе, последовательно слева направо выполняя умножения. Порядок нажатия клавиш показан на примере:

Запомним, что по схеме Горнера алгебраический многочлен n-ой степени можно вычислить за n операций умножения и n операций сложения. Это самый оптимальный способ вычисления.

Для перевода правильной дроби D из 10-ичной системы счисления в систему счисления с основанием p последовательно умножаем (в 10-ичной системе счисления) дробь D на основание системы счисления p.

Дробь в p-ичной системе счисления запишется в виде целых частей полученных произведений, начиная со старшего разряда. Целые части произведения в дальнейших операциях не используются.

Например: переводим в 2-ичную систему число 0.625 последовательным умножением на основание системы 2:

0,	625
1	250
0	500
1	000

Имеем результат: 0.625 ₁₀ = 0.101 ₂.

Умножение проводится до тех пор, пока дробная часть не станет равной 0 (как в примере) или не будет достигнута заданная точность перевода (заданное количество цифр после запятой, естественно, с отбрасыванием лишнего знака и округлением).

Для перевода правильной дроби из системы счисления с основанием p в 10-ичную систему счисления надо воспользоваться развернутой формой записи числа в системе счисления с основанием p. Например:

0.101 ₂ = 1*2^–1+ 0*2^–2 +1*2^–3 = 0.625 ₁₀.

Формы представления чисел

Представление чисел в памяти компьютера имеет некоторые особенности:

· ограниченная разрядная сетка компьютера приводит к ограничению диапазона представимых чисел;

· при выполнении операций умножения и сложения возможен выход за пределы разрядной сетки, так называемое переполнение.

Представление целых чисел

Целые числа при хранении в памяти могут занимать 1 байт, 2 байта, 4 байта. Наименьшее по абсолютной величине число, хранимое в ячейке памяти, равно нулю. Самое большое положительное число имеет такое представление (например, в однобайтовом представлении): 01111111₂ = 7F₁₆. В 10-ичной с/с это число равно
2⁷-1=127.

Если размер ячейки N битов, то максимальное целое положительное число, хранимое в ячейке, равно 2^N-1-1.

Логическое представление целых положительных чисел:

· Исходное целое число переводится в 16-ичную систему счисления (чтобы сократить количество операций деления).

· Полученное число из 16-ричной системы счисления переводится в 2-ичную систему счисления (каждый 16-ричный знак заменяется соответствующей ему тетрадой двоичных чисел).

· Записываем двоичное представление числа:

· Последовательно в битах справа налево записывается полученное двоичное представление числа.

· В крайнем слева бите записывается знак числа – в данном случае 0.

В оперативной памяти компьютера полученное представление числа располагается в перевернутом виде (от младшего байта к старшему).

Например:

256₁₀ = ?₂

256₁₀ = 0100₁₆ = 0000000100000000₂

Логическое представление	старший байт (с большим номером)								младший байт (с меньшим номером)
Номер разряда	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
Значение разряда	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0

В памяти это число хранится в виде: 0001₁₆

А как хранить отрицательные числа? Пусть имеем 4 бита памяти компьютера, выделяем один бит для хранения знака числа. Тогда, например, - 5 будет храниться как 1101, а 5 – как 0101. Диапазон представления чисел в этом случае будет уже не от 0 до 15, а от - 7 до 7, т. е. 15 различных значений (в 4 битах есть возможность хранить 16 различных последовательностей). Последовательность 1000 не задействована или, что еще более неприятно, она может трактоваться как - 0 , а это уже из разряда необъяснимых фактов, 0 и - 0.

Выполним инверсию и прибавление 1 к двоичному числу:

Число	Двоичное представление	Инверсия	Прибавление 1	Отрицательное число
1	0001	1110	1111	-1
2	0010	1101	1110	-2
3	0011	1100	1101	-3
4	0100	1011	1100	-4
5	0101	1010	1011	-5
6	0110	1001	1010	-6
7	0111	1000	1001	-7
8	1000	0111	1000	-8
0	0000	1111	10000	0

В предпоследнем столбце мы получаем двоичное представление отрицательных чисел. Все 16 двоичных последовательностей задействованы, диапазон представления от -8 до 7 и представление 0 однозначно. Представление отрицательных чисел в том виде, который приведен в таблице, называется дополнительным кодом. Представление положительных чисел в дополнительном коде совпадает с их обычным представлением.

Смысл понятия «дополнительный код» можно объяснить так: если Х – есть положительное целое число, представленное в N разрядах, а 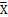– его дополнительный код, то справедливо:

Арифметическое устройство компьютера не умеет выполнять операцию вычитания. Вычитание сводится к сложению первого слагаемого с дополнительным кодом второго слагаемого. Это – конструкторская хитрость, позволяющая оптимизировать устройство процессора.

Максимальное по абсолютной величине целое отрицательное число, хранимое в ячейке памяти (например, в однобайтовом представлении), равно 10000000₂ = 80₁₆. В 10-ичной с/с это число равно -2⁷=-128.

Если размер ячейки N битов, то максимальное по абсолютной величине целое отрицательное число, хранимое в ячейке, равно -2^N-1.

Логическое представление отрицательных целых чисел (представление в дополнительном двоичном коде):

· Исходное число рассматривается как положительное и переводится в 16-ричную систему счисления.

· Полученное число из 16-ричной системы счисления переводится в 2-ичную систему счисления.

· Полученное представление числа инвертируется (нули заменяются единицами, а единицы – нулями).

· К полученному представлению добавляется 1 в самый младший разряд.

· Записываем двоичное представление числа:

· Последовательно в битах справа налево записывается полученное двоичное представление числа.

· В крайнем слева бите записывается знак числа – в данном случае 1.

В оперативной памяти компьютера полученное представление числа располагается в перевернутом виде (от младшего байта к старшему).

Например:

-256₁₀ = ?₂

256₁₀ = 0100₁₆ =100000000₂ = 0000000100000000

0111111011111111

+ 1

0111111100000000

Самый левый бит устанавливаем в 1, так как число отрицательное. Тогда имеем:

Логическое представление	Старший байт (байт с большим адресом)								Младший байт (байт с меньшим адресом)
Номер разряда	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
Значение разряда	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0

Логическое представление (в 16-ричной системе): FF 00 , в памяти – 00 FF .

Особенности целочисленной машинной арифметики:

преимущества (по сравнению с арифметикой вещественных чисел)

o целые числа всегда представимы своими точными значениями

o операции целочисленной арифметики всегда дают точные результаты

o операции целочисленной арифметики всегда выполняются быстрее, чем операции вещественной арифметики

· недостатки

o сравнительно узкий диапазон допустимых значений (для каждого типа свой)

o при выполнении программы автоматически не контролируется выход за этот диапазон (эффект переполнения), не происходит прерывания работы процессора и просто получается неверный результат.

o если есть опасность переполнения, то программист в программе должен сам предусматривать предупреждение этого.

Знак

Порядок (8 бит)

Мантисса (23 бита)

0 0 0 0 0 0 0 0 0 1, 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Порядок записывается со сдвигом, равным 2^8-1-1== 127 == 7 F ₁₆

Например:

-256,5₁₀ = ?

256₁₀ = 0100₁₆ =1 0000 0000₂

0,5₁₀ = 0.8₁₆ = 0.1000₂

-256,5₁₀ = -1 0000 0000 . 1000₂ = -1 . 0000 0000 1000₂ *2⁸

Формирование числа в 4-х байтах	Формирование числа в 8 байтах
Характеристика числа равна: 7F + 8 = 87₁₆ == 1000 0111₂	Характеристика числа равна: 3 F F + 8 = 407₁₆ == 100 0000 0111₂
Усеченная мантисса: 00 80 00 00₁₆ 0000 0000 1000 0000 0000 0000 ₂	Усеченная мантисса: 00 80 00 00 00 00 0₁₆
Полное представление числа: 1 1000 0111 0000 0000 1000 0000 0000 000 ₂= = 1100 0011 1000 0000 0100 0000 0000 0000 ₂= = С3 80 40 00 ₁₆	Полное представление числа: С0 70 08 00 00 00 00 00 ₁₆
В памяти число хранится в перевернутом (по байтам) виде: 00 40 80 С3	В памяти число хранится в виде: 00 00 00 00 00 08 70 С0

Диапазон вещественных чисел значительно шире диапазона целых чисел. Положительные и отрицательные числа расположены симметрично относительно нуля, значит, равны между собой по модулю.

Наименьшее по абсолютной величине число равно нулю. Наибольшее по абсолютной величине число в формате с плавающей точкой – это число с самой большой мантиссой и самым большим порядком.

Так как количество разрядов для представления мантиссы в памяти компьютера ограничено, то она в ряде случаев оказывается «обрезанной», т. е. дающей приближенное значение. Точное представление в компьютере имеет лишь дискретное конечное множество вещественных значений. Континуум действительных чисел отражается в машинном представлении на дискретное конечное множество.

Расстояние между двумя последовательными значениями на этом множестве зависит от количества разрядов, выделяемых под представление числа. Например, если под мантиссу выделяется 23 разряда, то следующее значение получается путем прибавления к мантиссе величины 2^-23., а если 52 разряда, то – 2^-52 .

Объясним, почему в случае:

float f=3123456.621f;

printf ("f= %f| f = %4.2f| f = %6.1f|\n", f, f, f);

Результат вывода:

f= 3123456.621000| f = 3123456.62| f = 3123456.6|

Представление звука

Согласно теории информации, носитель информации, используемый для передачи сообщений в системе связи – сигнал (им может быть любой физический процесс, параметры которого изменяются, или находятся, в соответствии с передаваемым сообщением). Информация передается посредством последовательностей сигналов по каналам связи. Канал связи – это протяженная в пространстве среда, через которую носитель сообщения передается от передатчика к приемнику.

Непрерывный сигнал – параметр сигнала есть непрерывная функция от времени.

Дискретный сигнал – параметр сигнала принимает последовательное во времени конечное число значений. Цифровой сигнал может изменяться лишь в определенные моменты времени и принимать лишь заранее обусловленные значения (например, только значения напряжений 0 и 3.5 В). Моменты возможного изменения уровня цифрового сигнала задает тактовый генератор конкретного цифрового устройства.

Для преобразования аналогового сигнала в цифровой сигнал требуется провести дискретизацию во времени и квантование по уровню.

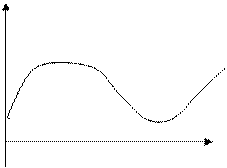
Дискретизация – замена непрерывного (аналогового) сигнала последовательностью отдельных во времени отсчетов этого сигнала. На Рис.1 схематично показан процесс преобразования аналогового сигнала в цифровой сигнал. Цифровой сигнал имеет в данном случае 5 уровней квантования, что обеспечивает невысокое качество преобразования. Изменение цифрового сигнала возможно лишь в определенные моменты времени (их на Рис.1 представлено 9). Показанный на рисунке слева непрерывный сигнал после преобразования заменяется числами 2-4-4-4-3-2-2-3-4. Совершенно очевидно, что чем больше уровней квантования и чем чаще во времени осуществляются отсчеты, тем точнее будет преобразован непрерывный сигнал в цифровой сигнал.

В соответствии со сказанным, различают две формы представления информации – непрерывную (аналоговую) и дискретную (цифровую). Непрерывная форма характеризует процесс, который не имеет перерывов и может изменяться в любой момент времени и теоретически на любую величину (например, речь человека, звучание музыкального произведения).

аналоговый сигнал

U U

к цифровой сигнал

у в

р а 4

о н

в т 3

е о

н в 2

ь а

н 1

t е 1 2 3 4 5 6 7 8 t

время дискретизация

Рис.1. Преобразование аналогового сигнала в цифровой сигнал

Для кодирования звука есть два основных параметра: частота дискретизации (измерение амплитуды сигнала через одинаковые промежутки времени) и битовая глубина кодирования (длина двоичного кода, который будет представлять в памяти компьютера амплитуду сигнала).

В графическом виде дискретизацию и квантование звука можно представить как переход от гладкой кривой к ломаной кривой. На примере показано трехразрядное квантование аналогового сигнала:

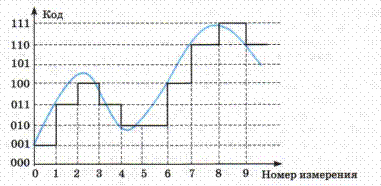
В память компьютера будет записана последовательность двоичных чисел: 001 011 100 100 010 010 100 110 111 110.

Объем записанной звуковой информации будет равен 3*10=30 битов. Если одно измеряемое значение занимает 8 разрядов (1 байт) памяти, то число уровней квантования равно 2⁸= 256, и точность измерения физической величины возрастает.