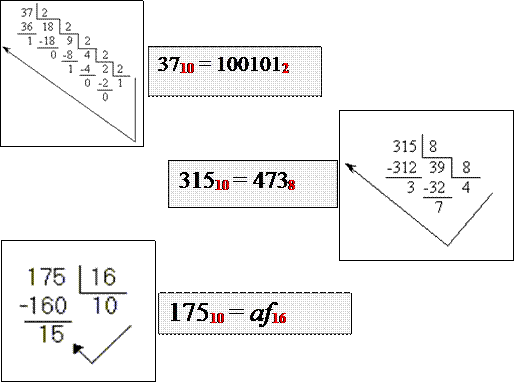
Для перевода целого числа из 10-ичной системы в систему с основанием p , надо выполнять последовательное деление числа (затем частных) на p до тех пор, пока не получится остаток меньше p. Число в новой системе счисления запишется в виде остатков от деления, начиная с младшего разряда результата. Последний остаток от деления даст старший разряд результата.

Пример перевода целого числа 19 из 10-ичной с/с в 2-ичную (последовательным делением на 2):

19	1	- младший разряд
9	1
4	0
2	0
1		- старший разряд

Таким образом, 19 ₁₀ = 10011 ₂

256 ₁₀ = ?₂ представить в двух байтах:

256 16

0    16 16

         0 1

256 ₁₀ = 100 ₁₆ = 0000000100000000 ₂ ;

1256 ₁₀ = ?₂ представить в двух байтах:                                         

1256 16

8      78 16

        14 4                       1 256₁₀ = 4Е8 ₁₆

1256 ₁₀ = 4Е8 ₁₆ = 0000 0100 1110 1000 ₂ = 0000010011101000 ₂

Для перевода целого числа из системы счисления с основанием  p в 10-ичную систему счисления используем развернутую форму записи числа в системе счисления с основанием p. Например:

11101₂ = 1*2⁴ + 1*2³ + 1*2² +1*2⁰=29₁₀.

Выполним перевод числа   DFF₁₆   в 10-ичную систему:

DFF₁₆ = D*16²  + F*16¹ + F*16⁰ = 13*16² + 15*16¹ + 15*16⁰ = 3583₁₀.

!!! Недесятичное число можно быстро перевести в 10-ичную с/с с помощью калькулятора. Для этого надо применить схему Горнера для вычисления алгебраических многочленов. Например:

231745₈ =2*8⁵ + 3*8⁴ + 1*8³ + 7*8² + 4*8¹ +5 =
 ((((2*8 + 3)*8 + 1)*8 + 7)*8 + 4)*8 + 5  = 78821₁₀

Скобочное выражение можно вычислить на калькуляторе, последовательно слева направо выполняя умножения. Порядок нажатия клавиш показан на примере:

Запомним, что по схеме Горнера алгебраический многочлен n-ой степени можно вычислить за  n операций умножения и n операций сложения. Это самый оптимальный способ вычисления.

Для перевода правильной дроби  D из 10-ичной системы счисления в систему счисления с основанием p последовательно умножаем (в 10-ичной системе счисления) дробь D  на основание системы счисления p.

Дробь в p-ичной системе счисления запишется в виде целых частей полученных произведений, начиная со старшего разряда. Целые части произведения в дальнейших операциях не используются.

Например: переводим в 2-ичную систему число 0.625 последовательным умножением на основание системы 2:

0,	625
1	250
0	500
1	000

Имеем результат: 0.625 ₁₀ = 0.101 ₂.

Умножение проводится до тех пор, пока дробная часть не станет равной 0 (как в примере) или не будет достигнута заданная точность перевода (заданное количество цифр после запятой, естественно, с отбрасыванием лишнего знака и округлением).

Для перевода правильной дроби из системы счисления с основанием p в 10-ичную систему счисления надо воспользоваться развернутой формой записи числа в системе счисления с основанием p. Например:

0.101 ₂ = 1*2^–1+ 0*2^–2 +1*2^–3 = 0.625 ₁₀.