Рассмотрим систему m линейных уравнений с n неизвестными:

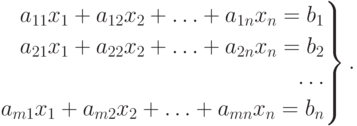
( 4.17)

Этой системе поставим в соответствие две матрицы. Первую

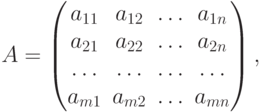
составленную из коэффициентов при неизвестных системы (4.17), называемую основной, и вторую

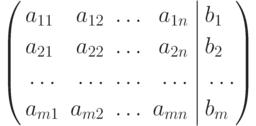
называемую расширенной матрицей системы (4.17).

ТЕОРЕМА (Кронекер и Капелли). Для того, чтобы система линейных уравнений (4.17) была совместной, необходимо и достаточно, чтобы ранг основной матрицы А был равен рангу ее расширенной матрицы В, то есть Rg A = Rg B.

Для системы (17) возможны следующие случаи:

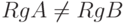1. . В этом случае система несовместна, то есть решений не имеет.
2. Rg A = Rg B = r. В этом случае система (4.17) совместна, то есть имеет хотя бы одно решение.

При этом:

если r = n ( n - число неизвестных), то система имеет единственное решение;

если r < n, то система имеет бесконечное число решений, которые находятся следующим образом:

• в матрице А выделяется любой базисный минор r -го порядка
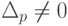
• выделяется подсистема, состоящая из уравнений, коэффициенты при неизвестных которых являются базисными строками или входят в минор ;
• полученная подсистема решается по формулам Крамера 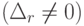при произвольных значениях (n - r) неизвестных, коэффициенты которых не входят в минор .

Пример 8. Решить систему

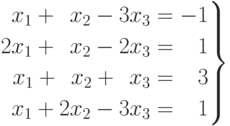
Решение. Составим основную

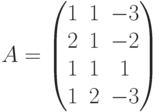
и расширенную

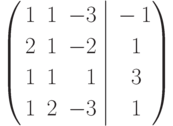
матрицы системы. Найдем Rg A и Rg B с помощью элементарных преобразований.

Анализируя решение получаем, что Rg A = 3, Rg B = 4, т.е. данная система несовместна.

Пояснения к РЕШЕНИЮ. При переходе от первой матрицы ко второй с помощью первой строки получены нули в первом столбце остальных строк; при переходе от второй матрицы к третьей поменяли местами третью и четвертую строки, при переходе от третьей к четвертой матрице с помощью второй строки получен нуль во втором столбце третьей строки; при переходе от четвертой матрицы к пятой с помощью третьей строки получен нуль в третьем столбце четвертой строки.

Пример 9: Исследовать на совместность и решить систему

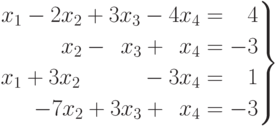
Решение. Составим основную и расширенную матрицы системы, соответственно:

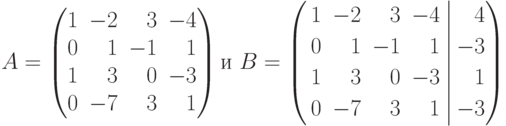
Как и в примере 8, найдем Rg A и Rg B с помощью элементарных преобразований матрицы В.

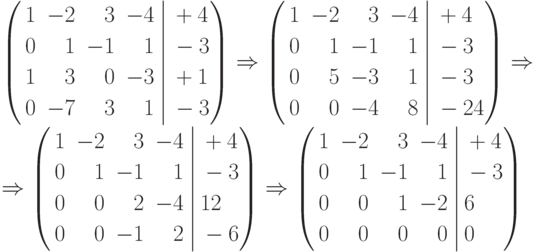
Очевидно, RgA = RgB = 3 < 4, где 4 - число неизвестных, т.е. система имеет бесконечное множество решений.

Составим подсистему, состоящую из первых трех уравнений:

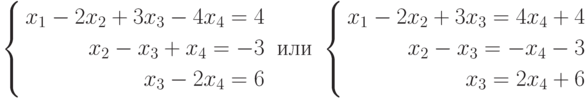
Последнее уравнение дает выражение для x₃ через x₄:x₃=2x₄+6. Подставив полученное x₃ во второе уравнение системы и приведя подобные получим выражение для x₂ через x₄:x₂=x₄+3. И, наконец, используя найденные x₃ и x₂, из первого уравнения найдем x₁:x₁=8. Таким образом имеем следующее множество решений: {(-8); (x₄+3); (2x₄+6)}, где x₄ - произвольная постоянная.

Пример 10: Исследовать и решить систему

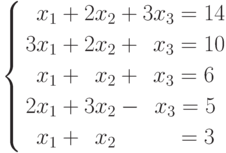
Решение. Составим основную и расширенную матрицы системы, соответственно:

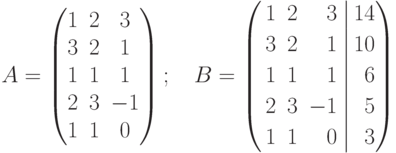
и применим к матрице В элементарные преобразования для приведения ее к треугольному виду:

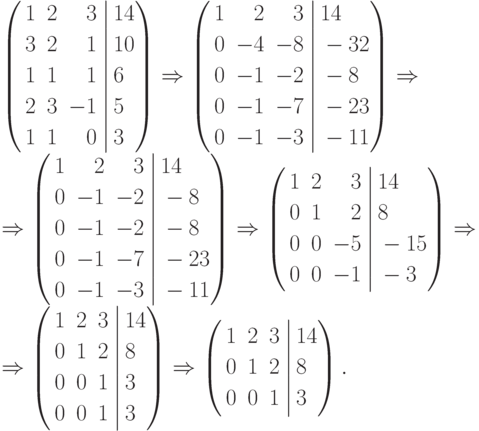
В матрице В пришлось вычеркнуть две строки, но полученная матрица приведена к треугольному виду. RgA = RgB = 3 = n ( n - число неизвестных), то есть система имеет единственное решение. Используя последнюю матрицу, запишем данную систему

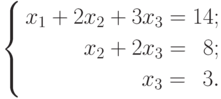
Решая систему, найдем x₃=3; x₂=2; x₁=1. Ответ (1, 2, 3).