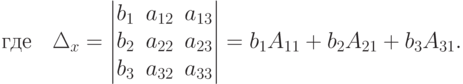Чтобы выяснить имеет ли составленная система решение или нет, а, если имеет решение, то их количество, применяют следующую теорему.

Теорема 1. Если ранг матрицы системы равен рангу расширенной матрицы системы, то такая система совместна и имеет хотя бы одно не нулевое решение.

Пример. Определить совместность системы

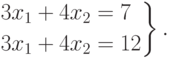
Решение. Составим матрицу системы 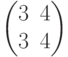и определим ее ранг (т.е. число независимых строк или столбцов:

Составим расширенную матрицу системы

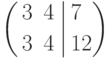
и определим ее ранг (т.е. число независимых строк или столбцов:

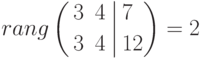
Как видим, ранг обычной матрицы не равен рангу расширенной, следовательно системы несовместна, т.е. не имеет ни одно решения.

Пример. Определить совместность системы

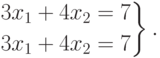
Решение. Составим матрицу системы

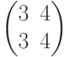
и определим ее ранг (т.е. число независимых строк или столбцов:

Составим расширенную матрицу системы

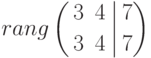
и определим ее ранг (т.е. число независимых строк или столбцов:

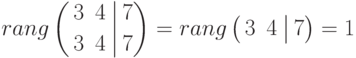
Как видим, ранг обычной матрицы равен рангу расширенной, следовательно системы совместна, т.е. имеет хотя бы одно решение.

Заметим, что положительный ответ на вопрос "совместна ли система?" не гарантирует единственность возможного решения.

Виды систем линейных уравнений.

Определение 5. Если система

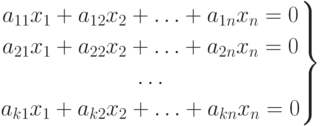
( 3.2)

совместна, то она имеет бесконечное множество ненулевых (невырожденных) решений и называется однородной системой.

Однородная система всегда совместна и всегда имеет хотя бы одно нулевое решение.

Определение 6. Если система имеет единственное нулевое решение, то такая система называется вырожденной.

Определение 7. Если система имеет количество уравнений меньшее, чем количество неизвестных, то такая система называется недоопределенной, а если количество уравнений больше, чем количество неизвестных, то – переопределенной.

Матрицы таких систем (недоопределенной и переопределенной) как правило прямоугольные. Решаются такие системы специальными методами, относящимися к разделу линейного программирования.

Лекция 5. Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ

Правило Крамера

Основные задачи изучения системы (3.1), "лекции 3" :

1. Выяснить, является ли система (3.1) совместной или несовместной.
2. Если система (3.1) совместна, то выяснить, является ли она определенной и найти решения.

Далее рассмотрим, в частности, систему трех уравнений первой степени с тремя неизвестными.

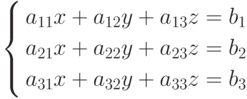
( 4.2)

Составим из коэффициентов при неизвестных системы (4.2) определитель этой системы

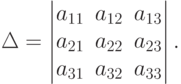
Умножим обе части первого уравнения почленно на алгебраическое дополнение А₁₁ элемента а₁₁, второе уравнение - на алгебраическое дополнение А₂₁ элемента а₂₁, а третье - на алгебраическое дополнение А₃₁ элемента а₃₁.

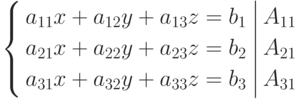
Сложим все три полученных уравнения, умножив предварительно на соответствующие алгебраические дополнения, получим

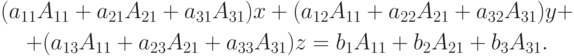
( 4.3)

Коэффициенты при y и z в силу свойства определителя (см. "лекц. 1" , теорема 2) равны

нулю, а коэффициент при х на основании тех же свойств (см. "лекц. 1" , теорема 1) равен , т.е. 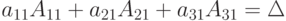, поэтому равенство (4.3) примет вид:

	( 4.4)
			( 4.5)

Заметим, что определитель получается из определителя путем замены коэффициентов а₁₁, а₂₁, а₃₁ при неизвестном х свободными членами или замены первого столбца коэффициентов при искомом х столбцом свободных членов. Аналогично получаются другие равенства:

( 4.6)

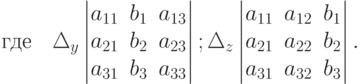
Определител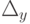и и получают из определителя системы заменой второго и третьего столбцов коэффициентов при y и z столбцом свободных членов.

Рассмотрим следующие случаи.

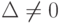1. . Тогда из равенств (4.4) и (4.5) находим решение системы (2) как

( 4.7)

1. которые называют формулами Крамера.
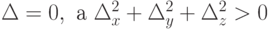2. . Тогда по крайней мере один из , 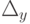или отличен от нуля и система (4.2) не имеет решения (система несовместна), что можно показать. Пусть, например, . Тогда равенство из (4.4) получаем или 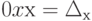, что невозможно.
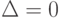3. и 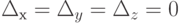. Тогда система (4.2) либо не имеет решения, либо имеет бесконечное множество решений.

Пример 1. Решить систему

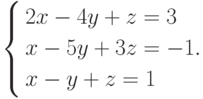
Решение. Вычислим все определители.

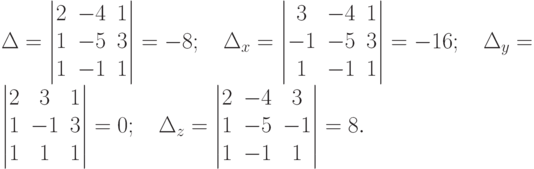
Так как 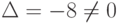, то данная система имеет единственное решение, которое найдем по формулам Крамера (4.7):

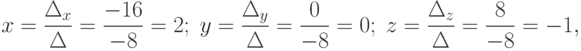
т.е. (2, 0, -1) - искомое решение системы.

Пример 2. Решить систему

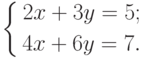
Решение. Вычислим определители

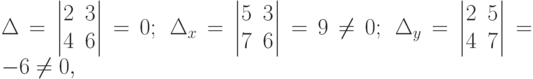
т.е. система решений не имеет (случай 2)

Пример 3. Решить систему

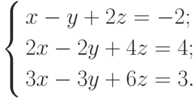
Решение. Нетрудно убедиться в том, что 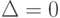и 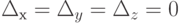. Данная система не имеет решений, так как первое и третье уравнения противоречивы. Если умножить первое уравнение на 3 и вычесть из полученного уравнение третье, то придем к ложному равенству 0 = 3.

Пример 4. Решить систему

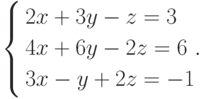
Решение. Нетрудно убедиться в том, что 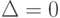и 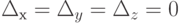. Так как второе уравнение получается из первого умножением на 2, то данная система равносильна системе двух уравнений относительно трех неизвестных

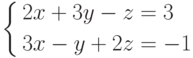
Так как

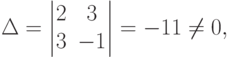
то можно найти решение последней системы

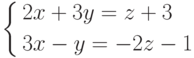
в которой переменная z является свободной, и, следовательно, исходная система имеет бесконечное множество решений, которое можно найти либо по формулам Крамера, либо методом исключений. В результате получим (-5z/11; (7z+11)/11; z), где z может принимать произвольные значения.