Рассмотрим определитель третьего порядка
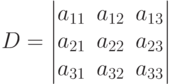
| ( 1.5) |
Вычеркнем из определителя одну строку и один столбец, например, первую строку и второй столбец. Из оставшиеся элементов составим определитель второго порядка
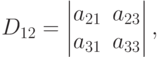
номер которого (индекс у D ) определяется номерами вычеркнутых строки (первой) и столбца (второй). Если из определителя (1.5) вычеркнуть другие строку и столбец, например, третий и третий, соответственно, то оставшиеся элементы будут также составлять определитель второго порядка, номер которого теперь будет другой - 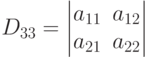
Определение 7. Определитель, который получается вычеркиванием одной строки и одного столбца из исходного определителя называется минором основного определителя.
Очевидно, что определитель третьего порядка имеет 9 различных миноров второго порядка, т.е. каждый элемент определителя имеет минор. Если взять определитель, например, пятого порядка, то количество миноров у такого определителя будет 25 – по количеству элементов (5 в строке и 5 столбцов). И эти миноры будут представлены определителями четвертого порядка.
Определение 8. Назовем алгебраическим дополнением любого элемента определителя D минор этого элемента, взятый со знаком плюс, если сумма номеров элемента четная и минус в противном случае
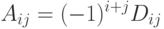
| ( 1.6) |
Пример. Выписать и вычислить все алгебраические дополнения определителя 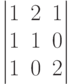 .
.
Решение. У определителя третьего порядка имеется 9 алгебраических дополнений (по каждому из элементов).
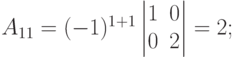
| 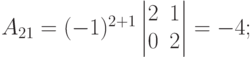
|
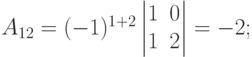
| 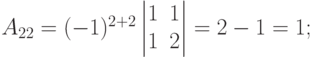
|
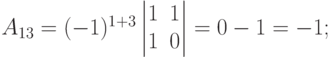
| 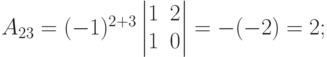
|
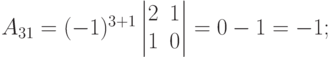
| 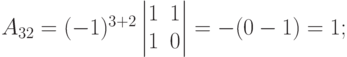
|
|
| |
Теорема 1. Определитель D равен сумме произведений элементов любого столбца или строки на их алгебраические дополнения
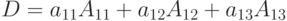
| ( 1.7) |
Очевидно, что для определителя третьего порядка можно записать шесть различных равенств (по трем столбцам и по трем строчкам).
Теорема 2. Суммы, произведений элементов для любого столбца (строки) на алгебраические дополнения другого столбца (строки) определителя, равна нулю.
Доказательство. Проведем доказательство на примере определителя (1.5). Возьмем сумму произведений алгебраических дополнений первой строки на элементы третьей строки. Получим
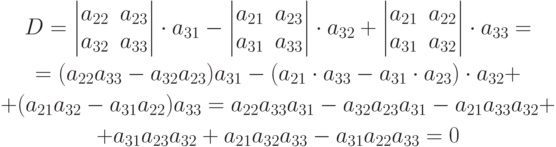
Разложение определителя по строке или столбцу дает нам правило вычисления любых определителей высоких порядков (четвертого и выше).
Определение 9. Определителем n -го порядка называется число  равное алгебраической сумме
равное алгебраической сумме
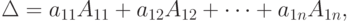
| ( 1.8) |
где Aij=(-1)i+jDij есть алгебраические дополнения элемента aij, а Dij - есть соответствующие миноры, т.е. определители ( n-1 )-го порядка, получающиеся из исходного определителя вычеркиванием первой строки и n -го столбца, на пересечение которых находится элемент aij.
Рассмотренные приемы позволяют вычислять определители любых порядков, а, следовательно, находить решение линейных систем любых порядков.
Пример. Вычислить определитель
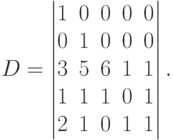
Решение. Для вычисления определителя пятого порядка воспользуемся формулой (1.8) и разложим данный определитель по первой строке (в этой строке все члены, кроме первого равны нулю). Получим
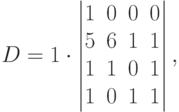
т.е. определитель стал теперь четвертого порядка. Опять разложим определитель по первой строке, так как все члены этой строки равны нулю, кроме одного. Затем вычислим полученный определитель третьего порядка по любой вычислительной схеме.
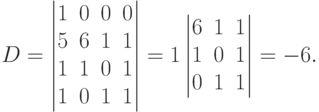
Лекция 2.
Матрицы. Основные определения и типы матриц
Определение 1. Матрицей A называется любая прямоугольная таблица, составленная из чисел aij, которые называют элементами матрицы и обозначается
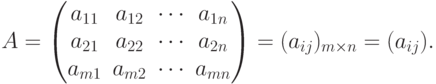
| ( 2.1) |
Заметим, что элементами матрицы могут быть не только числа. Представим себе, что вы описываете книги, которые стоят на вашей книжной полке. Пусть у вас на полке порядок и все книги стоят на строго определенных местах. Таблица, которая будет содержать описание вашей библиотеки (по полкам и следованию книг на полке), тоже будет матрицей. Но такая матрица будет не числовой. Другой пример. Вместо чисел стоят разные функции, объединенные между собой некоторой зависимостью. Полученная таблица также будет называться матрицей. Иными словами, Матрица, это любая прямоугольная таблица, составленная из однородных элементов. Здесь и далее мы будем говорить о матрицах, составленных из чисел.
Вместо круглых скобок для записи матриц применяют квадратные скобки или прямые двойные вертикальные линии
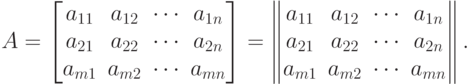
| ( 2.1*) |
Определение 2. Если в выражении (1) m = n, то говорят о квадратной матрице, а если 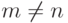 , то о прямоугольной.
, то о прямоугольной.
В зависимости от значений m и n различают некоторые специальные виды матриц:
- Матрица - строка (или строковая матрица), состоящая из одной строки. Это прямоугольная матрица размером 1 x n.
A=(a11 a12 ... an).
- Матрица - столбец ( столбцевая матрица), состоящая только из одного столбца. Это также прямоугольная матрица размером m x 1
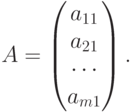
- Матрица, состоящая из одного элемента. A=(a11)1x1=a11.
- Нулевая матрица, состоящая из одних нулей, в матричной алгебре играет роль 0, обозначается V.
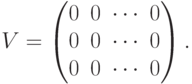
- Единичная матрица, состоящая из нулей, кроме главной диагонали, на которой стоят единицы. Обозначается E и играет роль единицы в матричной алгебре
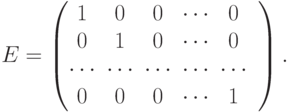
- Диагональная матрица, квадратная порядка n, состоящая из нулей и на главной диагонали стоят не равные нулю элементы (не обязательно единицы)
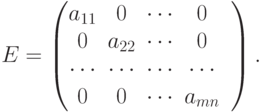
Важнейшей характеристикой квадратной матрицы является ее определитель или детерминант, который составляется из элементов матрицы и обозначается
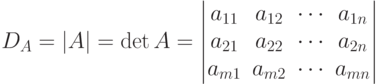
Очевидно, что DE=1 ; 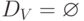 .
.
Определение 3. Если 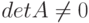 , то матрица A называется невырожденной или не особенной.
, то матрица A называется невырожденной или не особенной.
Определение 4. Если detA = 0, то матрица A называется вырожденной или особенной.
Определение 5. Две матрицы A и B называются равными и пишут A = B, если они имеют одинаковые размеры и их соответствующие элементы равны, т.е.
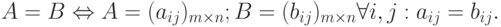
Например, матрицы 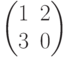 и
и 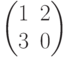 равны, т.к. они равны по размеру и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. А вот матрицы
равны, т.к. они равны по размеру и каждый элемент одной матрицы равен соответствующему элементу другой матрицы. А вот матрицы 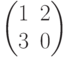 и
и 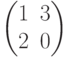 нельзя назвать равными, хотя детерминанты обеих матриц равны, и размеры матриц одинаковые, но не все элементы , стоящие на одних и тех же местах равны. Матрицы
нельзя назвать равными, хотя детерминанты обеих матриц равны, и размеры матриц одинаковые, но не все элементы , стоящие на одних и тех же местах равны. Матрицы 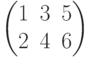 и
и 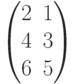 разные, так как имеют разный размер. Первая матрица имеет размер 2х3, а вторая 3х2. Хотя количество элементов одинаковое – 6 и сами элементы одинаковые 1, 2, 3, 4, 5, 6, но они стоят на разных местах в каждой матрице. А вот матрицы
разные, так как имеют разный размер. Первая матрица имеет размер 2х3, а вторая 3х2. Хотя количество элементов одинаковое – 6 и сами элементы одинаковые 1, 2, 3, 4, 5, 6, но они стоят на разных местах в каждой матрице. А вот матрицы 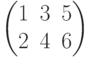 и
и 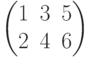 равны, согласно определению 5.
равны, согласно определению 5.
Определение 6. Если зафиксировать некоторое количество столбцов матрицы A и такое же количество ee строк, тогда элементы, стоящие на пересечении указанных столбцов и строк образуют квадратную матрицу n - го порядка, определитель которой 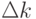 называется минором k – го порядка матрицы A.
называется минором k – го порядка матрицы A.
Пример. Выписать три минора второго порядка матрицы
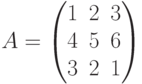
Решение. 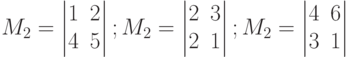 .
.
Матрицы. Ранг матрицы
Определение 7. Если матрица A не нулевая, т.е. существует хотя бы один aij элемент матрицы A, отличный от нуля, тогда всегда можно указать натуральное число r такое, что
- у матрицы A имеется минор r - го порядка, для которого
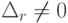 ;
; - всякий минор матрицы A порядка r+1 и выше равен нулю, тогда число r, обладающее указанными свойствами называетсярангом матрицы A и обозначается r = RgA.
Из определения 7 вытекает, что
- ранг любой прямоугольной матрицы не должен быть больше, чем минимальный размер матрицы. Если матрица квадратная, то ранг не может быть больше, чем размер матрицы. Математически это можно выразить так r<=min(m,n).
- если все элементы матрицы A равны нулю, т. е. aij=0, то ранг этой матрицы тоже будет равен нулю r = RgA = 0.
Понятие ранга матрицы играет очень важную роль при построении графиков, при нахождении решения системы линейных уравнений, при переходе от одного базиса к другому, а также широко используется в прикладных исследованиях, особенно при обработке результатов эксперимента, выделения аномалий и количественного определения качества предоставленной для изучения информации. Об этих и многих других задачах мы будем говорить несколько позже.
Определение 8. Всякий детерминант минора матрицы A, отличный от нуля, размер которого равен рангу этой матрицы, называется базисным минором. Т.е. иными словами ранг матрицы A это наивысший отличный от нуля минор.
Пример. Найти ранг матрицы
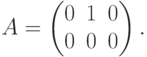
Решение. Так как в этой матрице только в одной строке есть отличные от нуля члены, то RgA=1.
Пример. Найти ранг матрицы
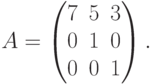
Решение. Для проверки найдем детерминант этой матрицы: detA=7. И так как он отличен от нуля,  , значит, ранг матрицы равен 3, т.е. в матрице нет пропорциональных строк или столбцов. В противном случае detA был бы равен нулю ( "лекция 1" , свойство 3).
, значит, ранг матрицы равен 3, т.е. в матрице нет пропорциональных строк или столбцов. В противном случае detA был бы равен нулю ( "лекция 1" , свойство 3).
Пример. Найти ранг матрицы
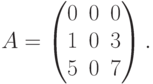
Решение. Очевидно, что detA=0, т.к. матрица содержит нулевую строку. Вычеркнем первую строку и второй столбец и найдем определитель полученного минора
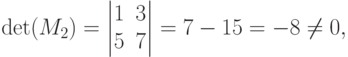
следовательно, делаем вывод, что RgA = 2.
Операции над матрицами
Определение 9. Суммой двух матриц одинакового размера A=(aij) и B=(bij) называется матрица C, у которой (cij)=(aij+bij), и записывают C = A + B.
Пример. Найти A + B, если
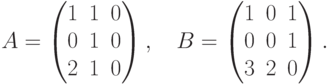
Решение.
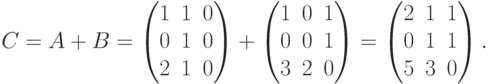
Можно убедится самостоятельно в справедливости равенств
- A + B = B + A ;
- (A + B) + C = A + (B + C).
Определение 10. Произведением матрицы A=(aij) на число k называется такая матрица C=(cij), у которой (cij) = (kaij).
Для операции произведение матрицы на число справедливы следующие соотношения:
- kA=Ak ;
- k(A+B)=Ak+Bk ;
-
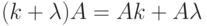 ;
; -
 .
.
Определение 11. Матрица B, у которой все элементы равны элементам матрицы A по абсолютной величине, но имеют противоположные знаки по сравнению со знаками соответствующих элементов матрицы A, называется противоположной матрице A и записывается B=(-1)(aij).
Заметим, что умножение любой матрицы на нулевую дает в результате нулевую матрицу, как и в обычной алгебре, т.е. 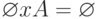 .
.
Если A - квадратная матрица, то тогда также очевидно равенство

где n - размер матрицы A.
Определение 12. Если A=(aij)mxp, а B=(bij)pxn, то произведением матрицы A на матрицу B назовем матрицу C, каждый элемент которой вычисляют по формуле:
C = AxB = (aij)mxpx(bij)pxn=(as1b1k+as2b2k+...+askbsk)mxn=(cij)mxn
Из определения 12 видно, что каждый элемент матрицы C = AB, расположенный в s -ой строке и k -ом столбце равен сумме произведений элементов s -ой строки матрицы A на элементы k -го столбца матрицы B.
При перемножении матриц можно воспользоваться следующей таблицей. Покажем это на примере.
Пусть требуется перемножить матрицы 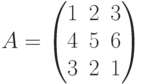 и
и 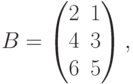 т.е. найти AB . Составим таблицу: слева запишем элементы матрицы А (которую умножают), а снизу – элементы матрицы В (на которую умножают):
т.е. найти AB . Составим таблицу: слева запишем элементы матрицы А (которую умножают), а снизу – элементы матрицы В (на которую умножают):
| 1 | 2 | 3 | ||
| 4 | 5 | 6 | ||
| 3 | 2 | 1 | ||
| 2 | 1 | |||
| 4 | 3 | |||
| 6 | 5 |
Результат будем записывать в выделенных ячейках, по формуле – сумма произведений соответствующих элементов:
| 1 | 2 | 3 | 1x2+2x4+3x6 | 1x1+2x3+3x5 |
| 4 | 5 | 6 | 4x2+5x4+6x6 | 4x1+5x3+6x5 |
| 3 | 2 | 1 | 3x2+2x4+1x6 | 3x1+2x3+1x5 |
| 2 | 1 | |||
| 4 | 3 | |||
| 6 | 5 |
Произведя вычисления, получаем:
| 1 | 2 | 3 | 28 | 22 |
| 4 | 5 | 6 | 64 | 49 |
| 3 | 2 | 1 | 20 | 14 |
| 2 | 1 | |||
| 4 | 3 | |||
| 6 | 5 |
Это и будет искомая матрица (в выделенных ячейках). Это способ очень наглядный и удобный, позволяет избежать ошибок при перемножении матриц.
Известны следующие очевидные свойства произведений матриц
- Переместительный закон не выполняется, т.е.
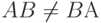 . Поэтому различают умножение на матрицу слева или справа;
. Поэтому различают умножение на матрицу слева или справа; - (A+B)C=AC+BC
- (AB)C=A(BC)=ABC
Определение 13. Если AB = BA, то такие матрицы A и B называют перестановочными или коммутативными.
Очевидно, что коммутативной с единичной будет любая матрица подходящего размера AE = EA = A.
Теорема. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц, т.е. det(AB) = detAxdetB.
Определение 14. Если в некоторой матрице A поменять местами столбцы и строки, то полученная матрица будет называться транспонированной и обозначается Aт.
Определение 15. Если выполняется равенство A = Aт, то такая матрица называется симметрической.
Определение 16. Обратной по отношению к матрице A называется такая матрица, для которой выполняется равенство AA-1 = A-1A = E.
Определение 17. Матрица, которая имеет обратную называется обратимой или не особенной.
Теорема. Для того, чтобы матрица A имела обратную матрицу A-1 необходимо и достаточно, чтобы она была бы невырожденной, т.е. 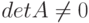 .
.
Доказательство. Необходимость. Пусть существует матрица A-1, тогда
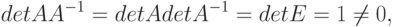
т.е. ни один из сомножителей не должен быть равен нулю, следовательно, 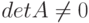 .
.
Достаточность. Пусть 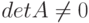 . Надо доказать, что существует обратная матрица A-1. Покажем это на примере квадратной матрицы третьего порядка. Пусть дана матрица
. Надо доказать, что существует обратная матрица A-1. Покажем это на примере квадратной матрицы третьего порядка. Пусть дана матрица
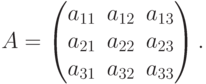
Найдем миноры второго порядка этой матрицы. Очевидно, что таких миноров будет 9: Ais = (-1)i+s Mis. Составим присоединенную матрицу из полученных алгебраических дополнений, которая обычно обозначается как
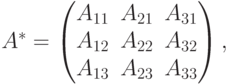
затем найдем произведение
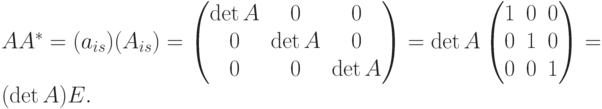
Т.е. AA*=(detA)E, следовательно  , откуда по определению обратной матрицы получаем
, откуда по определению обратной матрицы получаем
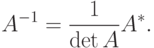
| ( 2.2) |
Теорема доказана. Заметим, что формула (2) известна как популярная расчетная формула для получения обратной матрицы.
Эта важная теорема дает нам простой алгоритм вычисления обратной матрицы, который можно сформулировать так.
- Вычислить detA ;1
- Вычислить все алгебраические дополнения матрицы A ;
- Найти обратную матрицу по формуле 2.
Пример. Найти обратную матрицу для 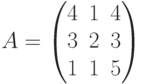 и выполнить проверку.
и выполнить проверку.
Решение. Вычисляем
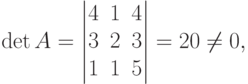
следовательно, обратная матрица существует. Найдем присоединенную матрицу A*. Для этого вычислим все миноры второго порядка матрицы A и алгебраические дополнения:
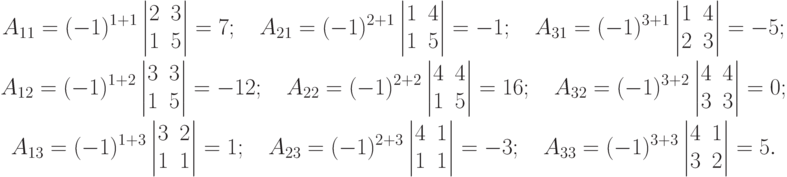
Составим
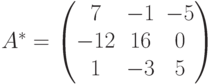
и найдем по формуле (2) обратную матрицу:
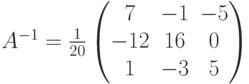
Проверка
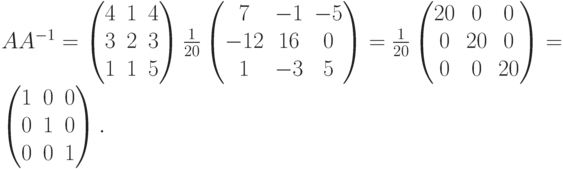
Дата: 2019-05-28, просмотров: 389.
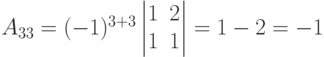 .
.