На практике редко задачи решаются при помощи таких простых систем, как рассмотренные в первом параграфе. Чаще для поиска решения получаются системы, состоящие из большего количества уравнений. Да и неизвестных в таких системах тоже больше, чем два. Пусть теперь дана система из трех линейных уравнений относительно трех неизвестных

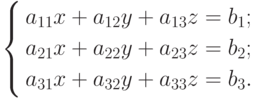
( 1.4)

Определение 6. Определителем третьего порядка, соответствующим матрице системы (1.4), назовем число D, равное

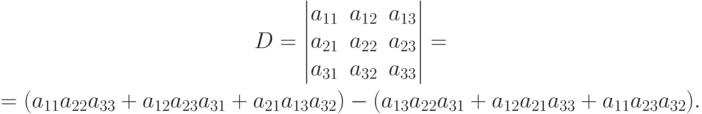
Для того, чтобы вычислить определитель третьего порядка применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот. Эти схемы известны как " правило треугольника " (или "правило звездочки") и " правило Саррюса ".

По правилу треугольника сначала перемножаются и складываются элементы, соединенными на схеме линиями

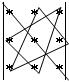
т.е. получаем сумму произведений: a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂.

Обратите внимание, что перемножаются элементы, соединенные одной линией, прямой или ломанной, а потом полученные произведения складываются.

Затем перемножаются и складываются элементы, соединенные на схеме

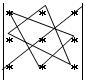
т.е. получаем другую сумму произведений a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂. И, наконец, чтобы вычислить определитель, из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:

D=(a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂)-(a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂).

По правилу Саррюса к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении и из нее вычитают сумму произведений элементов в другом направлении (см. схему):

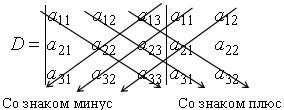
Можно убедиться, что результат будет таким же, что и при вычислении определителя по правилу треугольника.

Пример. Вычислить определитель

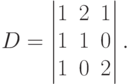
Решение. Вычислим определитель по правилу звездочки

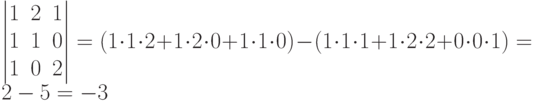
и по правилу Саррюса

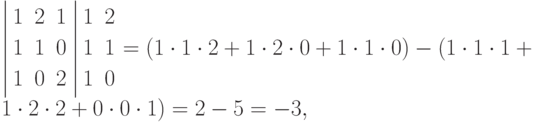
т.е. получаем одинаковый результат для обеих вычислительных схем, как и ожидалось.

Заметим, что все свойства, сформулированные для определителей второго порядка, справедливы для определителей третьего порядка, в чем можно убедиться самостоятельно. На основании этих свойств сформулируем общие свойства для определителей любого порядка.

Свойство 1. Величина определителя не изменяется при замене строк столбцами.

Свойство 2. При перестановке двух строк (столбцов) между собой, величина определителя меняет знак.

Свойство 3. Определитель с двумя одинаковыми (пропорциональными) строками (столбцами) равен нулю.

Свойство 4. Если все элементы некоторой строки (столбца) содержат одинаковый множитель, то этот множитель можно вынести за знак определителя.

Свойство 5. Если все элементы некоторой строки (столбца) есть сумма равного числа слагаемых, то определитель будет равен сумме определителей, в которых элементы указанной строки (столбца) записываются отдельными слагаемыми.

Свойство 6. Если все элементы некоторой строки (столбца) равны нулю, то весь определитель тоже равен нулю.

Свойство 7. Величина определителя не изменится, если к элементам некоторой строки (столбца) добавить соответствующие элементы другой строки(столбца), предварительно умножив их на один и тот же множитель.