Для того, чтобы переходить к построению функций импульсного отклика, необходимо убедиться, что все временные ряды стационарны. Для этого проверим обратные корни характеристического AR-полинома. Если VAR-модель стационарна, то все обратные корни меньше 1. Стационарность временных рядов позволит строить функции импульсного отклика. В нашей модели все корни меньше 1. (см. Рисунок 4)

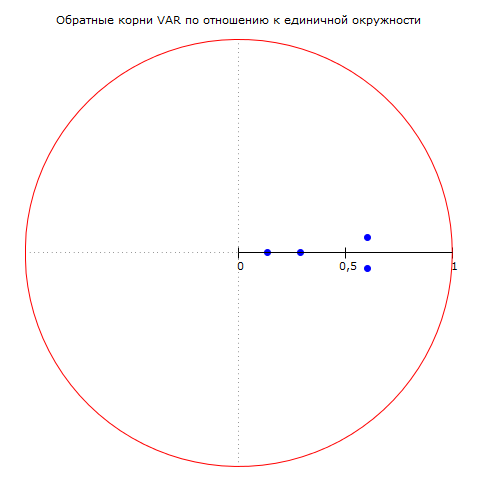
Рисунок 7 Значения обратных корней AR -полинома

Теперь рассмотрим импульсные отклики роста парниковых выбросов на шок в каждом факторе. Импульс – это однократное возмущение, которое придается одному параметру другим. Функция импульсного отклика предполагает временную реакцию динамического ряда. Функция импульсного отклика характеризует время возвращения эндогенной переменной на равновесную траекторию.

Импульсный отклик для фактора рост промышленности показывает, что шок происходит в текущий период и ведет к росту выбросов от 0,04 до 0,05 тонн на человека. Однако к третьему году влияние единичного шока заканчивается. (см. Рисунок 5)

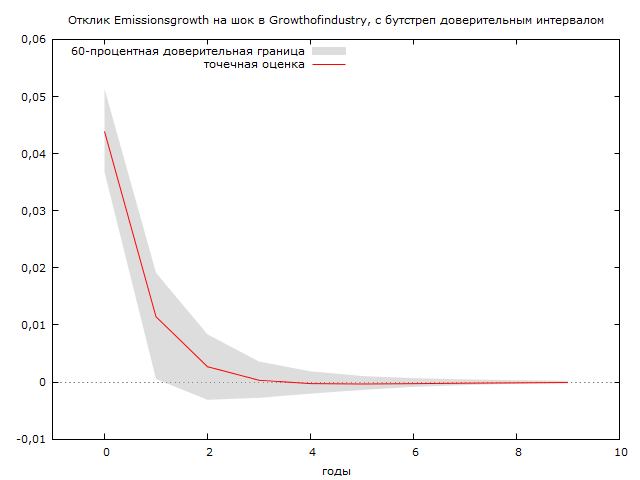
Рисунок 8 Импульсный отклик парниковых выбросов на рост промышленности

Импульсный отклик для фактора рост ВВП на душу населения показывает, что шок происходит в текущий период и ведет к росту выбросов от 0,025 до 0,035 тонн на человека. Однако данный шок имеет краткосрочное влияние и затухает уже к следующему году. Слабое влияние от единичного шока наблюдается в течение последующих 8 лет в диапазоне от 0 до 0,002 тонн на душу населения. (см. Рисунок 6)

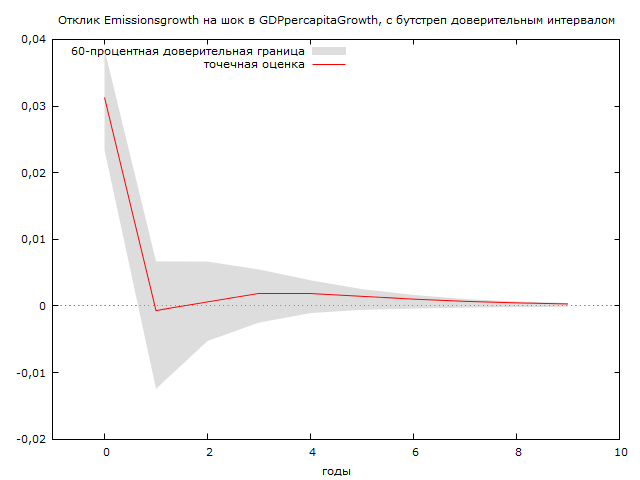
Рисунок 9 Импульсный отклик парниковых выбросов на рост ВВП на душу населения

Импульсный отклик для фактора доля возобновляемой энергии показывает, что шок происходит в текущий период и ведет к снижению выбросов в диапазоне от 0,003 до -0,015 тонн на человека. Эффект усиливается в следующем году и достигает -0,02 тонн на человека. Затем импульс постепенно стихает и достигает нуля в 9 году.

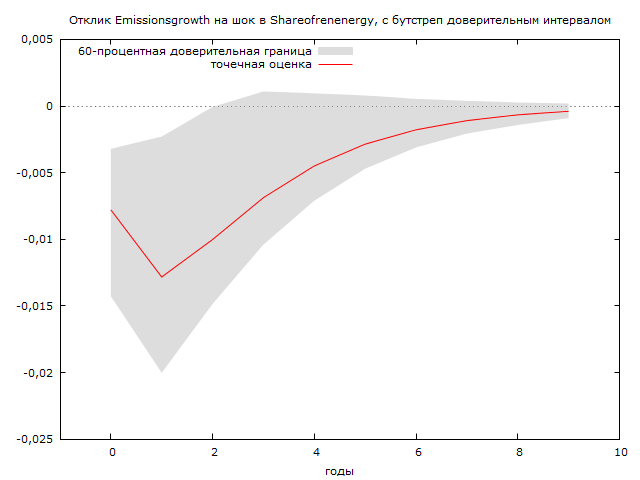
Рисунок 10 Импульсный отклик парниковых выбросов на изменение доли возобновляемых источников энергии

Наконец, отдельный интерес для данного исследования может представлять декомпозиция дисперсии. Она показывает вклад каждой из переменных в дисперсию прогноза исследуемого показателя. В нашей модели наибольший вклад в разложение дисперсий показателя «Парниковые выбросы» помимо лаговых значений данного параметра имеет экономический рост (около 30%) дисперсии прогноза ошибок. Его доля постепенно снижается, уступая дополнительные 5% показателю «Доля возобновляемых источников энергии».