ВЫБОР СПЕЦИФИКАЦИИ МОДЕЛИ
В качестве основной модели, описывающей зависимость парниковых выбросов от экономического роста, исследователи используют экологическую кривую Кузнеца. Используются эконометрические модели полнима второй степени, которые корректируются на некоторый фактор, также влияющий на выбросы.[18] В данном исследовании мы не исключаем предпосылки о том, что объемы выбросов определяются квадратичной функцией. Однако нас больше интересует, имеет ли экономический рост устойчивое долгосрочное влияние на парниковые выбросы.
Для анализа долгосрочного влияния текущих и прошлых значений временных рядов используем модель векторной авторегрессии (VAR-model). Векторные модели строятся относительно стационарных рядов и имеют неинтерпретируемые оцененные коэффициенты.[19]
Предположим, что производство в мире описывается производственной функцией Кобба-Дугласа, которая имеет вид:
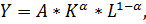 (1)
(1)
в которой A – уровень технологического развития, K – капитал, L – труд, 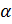 – эластичность по капиталу,(
– эластичность по капиталу,( 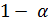 ) – эластичность по труду. [20]
) – эластичность по труду. [20]
В таком случае зависимость между парниковыми выбросами и экономическим ростом опивается следующим уравнением:
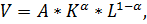 (2)
(2)
где 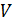 – суммарные выбросы парниковых газов в атмосферу.
– суммарные выбросы парниковых газов в атмосферу.
Предположим, что изменения в трудоспособным населении является величиной заданной экзогенными, то есть теоретически нет возможности влиять на её величину. Найдем уровень производства, приходящийся на одного работника. Он будет представлен как произведение уровня технологий и производства:
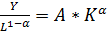 (3)
(3)
В терминах показателей национальных счетов 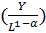 может быть приближен к значению ВВП в пересчете на душу населения. Другими допущениями могут считаться допущение о линейной однородности функции Кобба-Дугласа, то есть о постоянной отдаче от масштаба при изменении объемов производства.
может быть приближен к значению ВВП в пересчете на душу населения. Другими допущениями могут считаться допущение о линейной однородности функции Кобба-Дугласа, то есть о постоянной отдаче от масштаба при изменении объемов производства.
В таком случае зависимость между выбросами и экономическим ростом может быть представлена в виде:
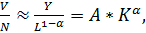 (4)
(4)
Однако рисунке 1 видно, что рост ВВП на душу населения лишь опосредованно связан с экономическим ростом. Так, можно выделить три основных тренда динамики парниковых выбросов на душу населения. Первый длится с 1960 по 1980 он стремительным ростом выбросов на 44%. После некоторого сокращения выбросов в начале 1980-ых годов объем выбросов на душу населения стагнировал и продолжил рост с 2000-ых годов.
В то же время ВВП на душу населения стремительно рос с небольшими периодами стагнации в начале 80-ых и 90-ых годах прошлого века.
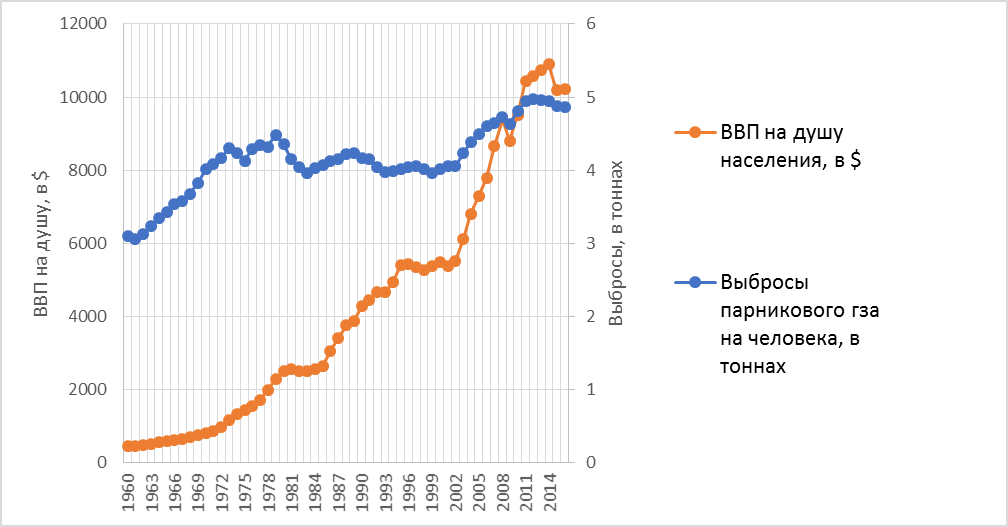
Рисунок 4 Динамика ВВП и выбросов парниковых газов на душу населения
Источник: World Bank Group
Очевидно, что оба ряда имеют тренд и не являются стационарными. Для доказательства построим коррелограмму для двух временных рядов – выбросов парникового газа и ВВП на душу населения, и проведем расширенный тест Дики – Фуллера.

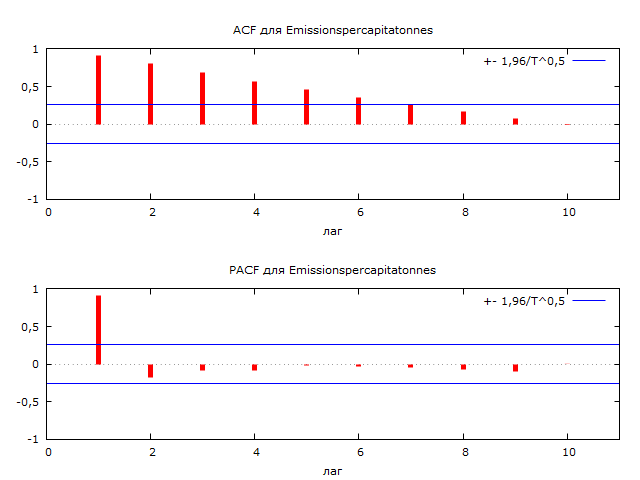
Рисунок 5 Расширенный тест Дики-Фуллера и коррелограмма для выбросов парникового газа
Источник: составлено автором в Gretl
Коррелограмма данного ряда говорит о том, что ряд является нестационарным, так как значение AC в первом лаге близко к 1, а коррелограммы убывают медленно – лишь к 10 лагу. Тест Дики-Фуллера, тестирующий нулевую гипотезу о нестационарности ряда при пятипроцентном уровне значимости показывает, что значение статистики больше критического значения (p-value равно 0,3769). Следовательно, нулевая гипотеза о нестационарности ряда принимается. (см. Рисунок 2)


Рисунок 6 Расширенный тест Дики-Фуллера и коррелограмма для ВВП на душу населения
Источник: составлено автором в Gretl
Коррелограмма ряда «ВВП на душу населения» говорит о том, что ряд также является нестационарным, так как значение AC в первом лаге близко к 1, а коррелограммы убывают медленно. Тест Дики-Фуллера, тестирующий нулевую гипотезу о нестационарности ряда при пятипроцентном уровне значимости показывает, что значение статистики больше критического значения (p-value равно 0,5399). Следовательно, нулевая гипотеза о нестационарности ряда принимается. (см. Рисунок 3)
Для того, чтобы сделать временной ряд стационарным, используем значения первых разностей для исследуемых показателей. Таким образом, новые значения будут иметь вид: 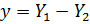 и
и 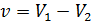 , где
, где 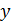 и
и 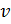 – абсолютное изменение соответствующих показателей.
– абсолютное изменение соответствующих показателей.
В то же время количественные (денежные показатели) агрегированные показатели ВВП на душу населения не учитывают его качественные характеристики, которые также могут определять динамику парниковых выбросов. В моделях, исследующих зависимость между экономическим ростом и выбросами парниковых газов, необходимо учитывать неколичественные факторы. К ним могут относиться отраслевая структура мировой экономики, степень развития технологий, качество политических и экономических институтов, международные соглашения[21], а также структура мировой энергетики. [22]
Ранее было описано, что промышленность является одним из основных источников выбросов углекислого газа. Более 30% выбросов приходится на промышленность, 20% на строительство и недвижимость и 15-20% на топливно-энергетический комплекс. [23] По этой причине вторым важным компонентом является структура мировой энергетики: гипотеза состоит в том, что между выбросами и долей возобновляемой энергетики обратная связь. Так как сжигание ископаемых источников энергии в процессе производства служит источником выбросов углекислого газа.
Таким образом, векторная регрессия VAR(p) будет иметь следующий вид:
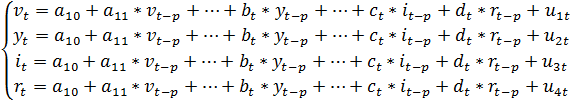 (5)
(5)
где 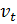 – первая разность выбросов парниковых газов на душу населения за период t,
– первая разность выбросов парниковых газов на душу населения за период t,
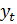 - первая разность ВВП на душу населения за период t,
- первая разность ВВП на душу населения за период t,
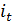 – рост промышленности в t-ый период,
– рост промышленности в t-ый период,
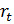 – первая разность доли возобновляемой энергетики в структуре производства энергии в мире за t-ый период;
– первая разность доли возобновляемой энергетики в структуре производства энергии в мире за t-ый период;
Выбор порядка лага модели осуществлялся на основании трех критериев – BIC, AIC и HQS. По результатам тестирования наилучшим порядком лага оказался первый лаг по всем трем критериям. (см. Таблица 1)
Таблица 2 Выбор лагов для VAR
| Номер лага | AIC | BIC | HQС |
| 1 | 18,190399* | 18,947978* | 18,479893* |
| 2 | 18,372924 | 19,736565 | 18,894011 |
| 3 | 18,521960 | 20,491665 | 19,274642 |
| 4 | 18,748822 | 21,324590 | 19,733099 |
Примечание: Звездочкой отмечены наилучшие (минимальные) значения лагов
Последним этапом, предшествующим получению результатов моделирования, является проведение теста Грэнджера, суть которого состоит в том, чтобы проверить гипотезу о наличии причинно-следственных связей между временными рядами. Так как нас интересует лишь одно направление причинно-следственной связи – фактор «X» является причиной для роста парниковых выбросов, то мы проверим лишь первую часть гипотез, проверяющих причинность этого типа. Рассчитаем F-статистики попарно для каждого регрессора при лаге 1.
Таблица 3 Результаты теста Грэнджера
| Направление | F-статистика | p-value | Результат |
| y → v | 2,1274 | 0,0913 | Принимается (на 10% интервале) |
| r → v | 2,3299 | 0,0872 | Принимается (на 10% интервале) |
| i → v | 3,4721 | 0,0173 | Принимается |
Результаты моделирования показали, что наиболее значимым является показатель роста промышленности, так как его значения принимаются на 5% доверительном интервале. Другие показатели также влияют на выбросы, но принимаются на большем доверительном интервале.
Дата: 2019-05-28, просмотров: 410.