Расчёт на прочность производим по максимальным погонным усилиям.

Определяем напряжения в нижнем полюсе бака: ,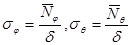

где 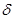– толщина стенки бака.

Подставив в эти формулы выражения для погонных меридиональных и кольцевых усилий, получим:

.

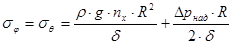Минимальную толщину оболочки можно получить по формуле:

,

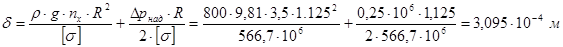где  – допускаемые напряжения.

Определяем массу оболочки бака:

,

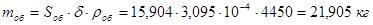где 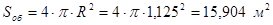 – площадь поверхности оболочки;

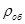– плотность материала оболочки.

Построим эпюру погонных усилий ,  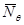(рис. 3):

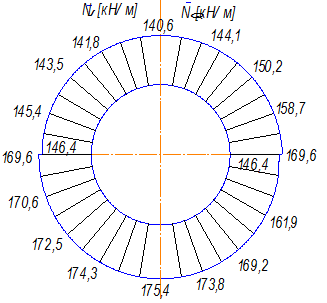
Рис. 3. Эпюра погонных усилий ,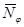

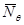
РАСЧЁТ БАКА НА ПРОЧНОСТЬ

Условие задачи: Цилиндрический бак с верхним полуэллиптическим и нижним полусферическими днищами (рис.1) находится под действием давления наддува  и заполнен жидкостью до уровня H.

Цель расчёта:

1. Определить величину безмоментных напряжений ;

2. Определить толщину обечайки и днищ бака.

Исходные данные:

Радиус бака: 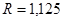            м;

Размеры эллиптического днища: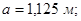

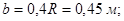
Высота столба жидкости: ;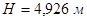

Плотность жидкости (окислитель):    ;

Давление наддува: ;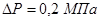

Коэффициент безопасности:     ;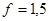

Материал оболочки:

марка             ВТ6С (О);

предел прочности   ;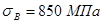

.

Выполнение расчёта

Участок верхнего эллиптического днища

Рис. 2. Схема эллиптического днища

В днище нормальным коническим сечением I – I отсечём верхнюю часть оболочки и составим для неё уравнение равновесия. Выбираем оси координат так, как показано на рис. 2. Из уравнения равновесия и уравнения Лапласа получаем выражения для  в расчётном сечении эллиптического днища в виде:

,

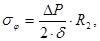
где 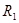, 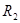– радиусы кривизны рассматриваемого сечения оболочки,

,

,

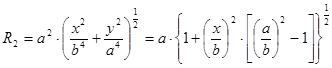где x, y – координаты точки в рассматриваемом сечении оболочки.

Для построения эпюр задаёмся значениями x. Координату y определяем из уравнения эллипса 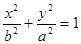. Отсюда получаем

.

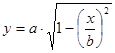Меньшую полуось b разбиваем на 5 равных частей, для каждого сечения производим расчёты, результаты расчётов заносим в таблицу 1.

Таблица 1

№ сечения	x , м	y , м	R1, м	R2, м	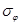, МПа	, МПа
1	0	1,125	0,18	1,125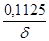
2	0,09	1,102	0,24	1,238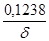
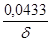
3	0,18	1,031	0,449	1,526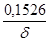
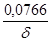
4	0,27	0,9	0,884	1,913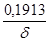
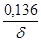
5	0,36	0,675	1,639	2,349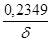
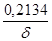
6	0,45	0	2,813	2,813

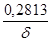
Участок цилиндра над зеркалом жидкости

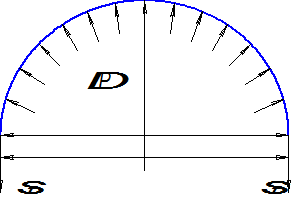
Рис. 3. Сечение II – II

Нормальным сечением к оси бака II – II отсечём часть цилиндра, расположенную над зеркалом жидкости (рис. 3). Составим уравнение равновесия для верхней отсеченной части оболочки в проекции на вертикальную ось:

.

Отсюда меридиональное напряжение:

 Па.

Для цилиндра 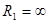; 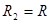, поэтому из уравнения Лапласа получаем кольцевое напряжение:

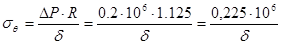 Па.