Условие задачи: Построить эпюры безмоментных напряжений 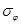 и
и 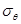 для сферического сосуда (рис. 1), полностью заполненного жидкостью.
для сферического сосуда (рис. 1), полностью заполненного жидкостью.
Исходные данные:
Радиус оболочки: 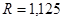 м;
м;
Плотность жидкости (окислитель):
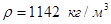 ;
;
Толщина стенки оболочки:
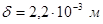 .
.
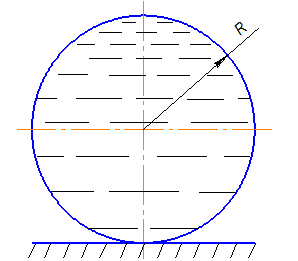
Рис. 1. Схема оболочки
Выполнение расчёта
Выводы расчётных зависимостей для верхней полусферы
В верхней полусфере отсечём часть оболочки нормальным коническим сечением с углом 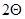 при вершине конуса и составим уравнение равновесия отсеченной части оболочки (рис. 2):
при вершине конуса и составим уравнение равновесия отсеченной части оболочки (рис. 2):
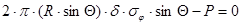 ,
,
где 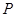 – равнодействующая сил давления жидкости
– равнодействующая сил давления жидкости 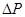 на стенку оболочки в проекции на
на стенку оболочки в проекции на
вертикальную ось.
Жидкость действует на стенку оболочки переменным давлением. Равнодействующую сил давления жидкости на вертикальную ось определим по формуле:
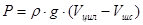 ,
,
где 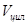 – объём цилиндра;
– объём цилиндра; 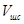 – объём шарового сегмента, рис. 2.
– объём шарового сегмента, рис. 2.
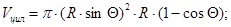
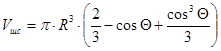 ,
,
где 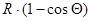 - высота столба жидкости в расчётном сечении.
- высота столба жидкости в расчётном сечении.
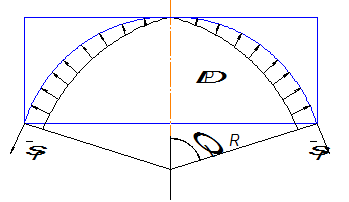
Рис. 2. Расчётная схема
Получаем:
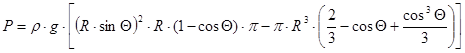 .
.
Из уравнения равновесия после подстановки выражения для силы 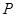 имеем:
имеем:
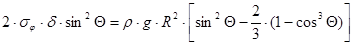 .
.
Отсюда меридиональное напряжение:
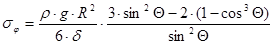 .
.
Определим кольцевое напряжение 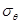 . Для этого обратимся к уравнению Лапласа, учитывая, что для сферической оболочки R 1 = R 2 = R::
. Для этого обратимся к уравнению Лапласа, учитывая, что для сферической оболочки R 1 = R 2 = R::
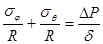 ,
,
где 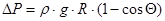 - давление жидкости в рассматриваемом сечении оболочки.
- давление жидкости в рассматриваемом сечении оболочки.
После подстановки в уравнение Лапласа 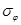 получаем:
получаем:
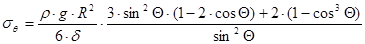 .
.
Принимая угол 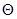 в диапазоне от 0˚ до 90˚, занесём значения составляющих уравнения равновесия, кольцевых и меридиональных напряжений с шагом угла
в диапазоне от 0˚ до 90˚, занесём значения составляющих уравнения равновесия, кольцевых и меридиональных напряжений с шагом угла 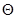 , равным 10˚,в таблицу 1.
, равным 10˚,в таблицу 1.
Таблица 1
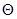 , град. , град.
| 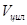 л, м3 л, м3
| 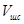 , м3 , м3
| 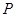 , Н , Н
| 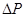 , Па , Па
| 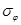 , Па , Па
| 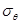 , Па , Па
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0,002049 | 0,001027 | 11,445 | 191,409 | 2,442 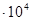
| 7,350 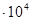
|
| 20 | 0,032 | 0,016 | 174,869 | 759,818 | 9,616 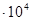
| 2,925 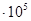
|
| 30 | 0,15 | 0,077 | 818,854 | 1688 | 2,107 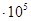
| 6,528 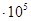
|
| 40 | 0,432 | 0,226 | 2314 | 2948 | 3,603 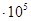
| 1,148 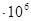
|
| 50 | 0,938 | 0,503 | 4870 | 4501 | 5,338 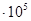
| 1,768 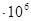
|
| 60 | 1,677 | 0,932 | 8349 | 6300 | 7,161 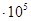
| 2,506 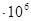
|
| 70 | 2,599 | 1,512 | 12170 | 8290 | 8,869 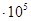
| 3,354 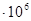
|
| 80 | 3,585 | 2,213 | 15360 | 10410 | 1,019 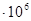
| 4,307 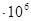
|
| 90 | 4,473 | 2,982 | 16700 | 12600 | 1,074 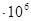
| 5,371 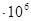
|
Выводы расчётных зависимостей для нижней полусферы
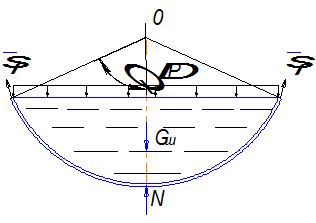
Рис. 3. Расчётная схема
Отсечём нормальным коническим сечением часть сферы (рис. 3). Вес жидкости в объёме шарового сегмента 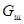 и равнодействующая от гидростатического давления жидкости
и равнодействующая от гидростатического давления жидкости 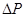 , находящейся выше рассматриваемого сечения, уравновешиваются реакцией опоры N и результирующим меридиональным усилием от погонных меридиональных сил, распределённых по круговому контуру шарового сегмента в сечении
, находящейся выше рассматриваемого сечения, уравновешиваются реакцией опоры N и результирующим меридиональным усилием от погонных меридиональных сил, распределённых по круговому контуру шарового сегмента в сечении 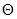 . Отсюда получим следующее уравнение равновесия:
. Отсюда получим следующее уравнение равновесия:
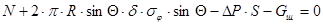 ,
,
где 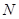 - реакция опоры, равная весу жидкости в объёме шара.
- реакция опоры, равная весу жидкости в объёме шара.
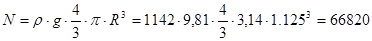 Н;
Н;
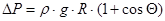 - гидростатическое давление жидкости;
- гидростатическое давление жидкости;
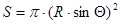 - площадь поперечного сечения;
- площадь поперечного сечения;
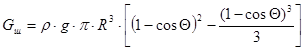 - вес жидкости в объёме шарового сегмента.
- вес жидкости в объёме шарового сегмента.
После подстановки получим:
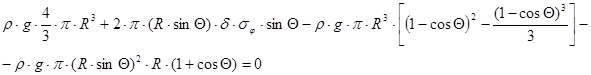
Отсюда имеем:
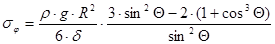 .
.
Для нижней части полусферы 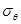 определяем из уравнения Лапласа:
определяем из уравнения Лапласа:
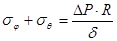 , где
, где 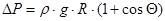 .
.
Отсюда:
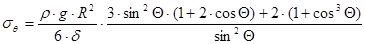 .
.
Принимая угол 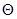 в диапазоне от 90˚ до 0˚, занесём значения составляющих уравнения равновесия, кольцевых и меридиональных напряжений с шагом угла
в диапазоне от 90˚ до 0˚, занесём значения составляющих уравнения равновесия, кольцевых и меридиональных напряжений с шагом угла 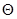 , равным 10˚,в таблицу 2.
, равным 10˚,в таблицу 2.
Таблица 2
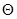 , град. , град.
| 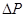 , Па , Па
| S, м2 | 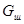 , Н , Н
| 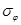 , Па , Па
| 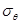 , Па , Па
|
| 90 | 12600 | 3,976 | 33410 | 1,074 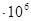
| 5,371 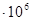
|
| 80 | 14790 | 3,856 | 24790 | 9,958 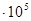
| 6,568 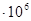
|
| 70 | 16910 | 3,511 | 16940 | 6,922 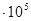
| 7,957 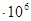
|
| 60 | 18910 | 2,982 | 10440 | -1,908 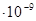
| 9,667 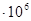
|
| 50 | 20700 | 2,333 | 5633 | -1,411 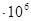
| 1,2 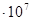
|
| 40 | 22260 | 1,643 | 2529 | -4,314 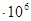
| 1,57 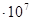
|
| 30 | 23520 | 0,994 | 859,303 | -1,095 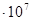
| 2,298 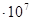
|
| 20 | 24450 | 0,465 | 178,593 | -3,038 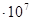
| 4,288 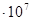
|
| 10 | 25020 | 0,12 | 11,508 | -1,361 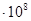
| 1,489 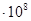
|
| 0 | 25210 | 0 | 0 | -1,362 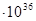
| 1,362 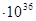
|
Выводы
В опорной точке сферы безмоментные напряжения обращаются в бесконечность. Это является следствием обращения в ноль площади сечения, по которой действуют напряжения 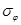 . В реальных условиях сосредоточенных в точке сил не существует, и поэтому эта особенность имеет место лишь в расчётной схеме.
. В реальных условиях сосредоточенных в точке сил не существует, и поэтому эта особенность имеет место лишь в расчётной схеме.
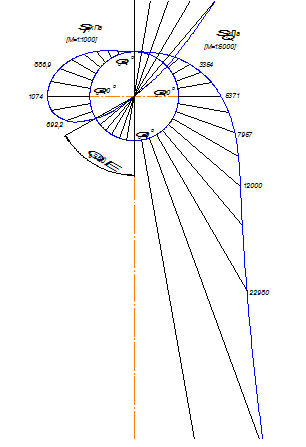
Рис. 4. Эпюра напряжений 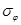 и
и 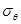
Дата: 2019-05-28, просмотров: 340.