Рассмотрим участок оболочки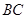 
(рис. 1). На расстоянии 
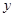от полюса 
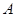отсекаем часть оболочки нормальным коническим сечением с углом широты 
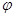(рис. 2).
1.1 Определяем границы участка BC: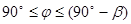 
.
1.2 Составляем уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось для отсечённой части оболочки:
,
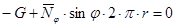где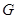 
- вес жидкости, заполняющей полусферу; 
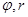- координаты расчётного сечения; 
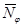- меридиональная погонная сила.
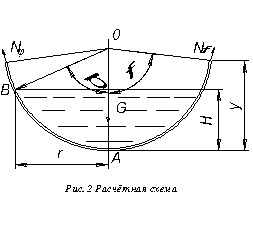
1.3 Определяем высоту столба жидкости в полусферической оболочке:
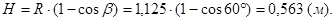
1.4 Находим объём шарового сегмента, заполненного жидкостью:
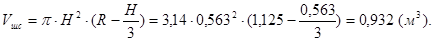
1.5 Вычисляем вес жидкости по формуле:
1.6 Определяем текущий радиус кольцевого сечения оболочки:
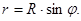
1.7 Находим погонное меридиональное усилие 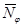из уравнения равновесия отсечённой части оболочки:
.
1.8 Определяем погонное кольцевое усилие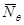 
для участка 
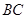, используя уравнение Лапласа:
,
где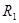 
, 
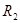– главные радиусы кривизны расчётного сечения оболочки;
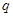– интенсивность внешней нагрузки на стенку в расчётном сечении оболочки.
Для сферы R1 = R2 и для участка 
= - 
.
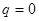
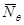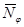Результаты расчёта заносим в таблицу 1 при условии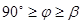 
.
Таблица 1
| № точки |  , град.
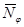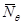| , Н/м
|  , Н/м
|
| 1 | 90 | 1035 | -1035 |
| 2 | 87 | 1037 | -1037 |
| 3 | 84 | 1046 | -1046 |
| 4 | 81 | 1061 | -1061 |
| 5 | 78 | 1081 | -1081 |
| 6 | 75 | 1109 | -1109 |
| 7 | 72 | 1144 | -1144 |
| 8 | 69 | 1187 | -1187 |
| 9 | 66 | 1240 | -1240 |
| 10 | 63 | 1303 | -1303 |
| 11 | 60 | 1380 | -1380 |
Расчёт участка оболочки под уровнем жидкости
Рассмотрим участок оболочки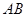 
(рис.1). Построим нормальное коническое сечение на расстоянии 
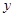от полюса оболочки. Положение расчётного сечения определяется углом широты
2.1 Определим границы участка :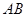 
.
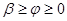2.2 Составляем уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось для отсечённой части оболочки:
,
где 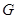- вес жидкости, заключённой в шаровом сегменте высотой ; 
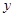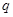- давление жидкости в расчётном сечении; 
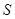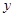- площадь поперечного сечения оболочки на уровне ; 
- радиус поперечного сечения оболочки на уровне .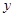
2.3 Определяем составляющие уравнения равновесия:
Объём шарового сегмента:
,
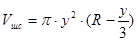где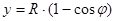 
.
Вес жидкости: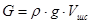 
.
Давление жидкости на уровне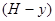 
от зеркала жидкости:
.
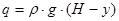Площадь поперечного сечения
,
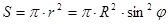где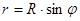 
.
Значения составляющих уравнения равновесия заносим в таблицу 2.
Таблица 2
| № точки | , град.
| Vшс, м3 | G, Н | q, Па | S, м2 | r, м |
| 1 | 60 | 0,932 | 7313 | 0 | 3,443 | 0,974 |
| 2 | 54 | 0,656 | 5145 | 775,06 | 3,217 | 0,910 |
| 3 | 48 | 0,436 | 3419 | 1493 | 2,955 | 0,836 |
| 4 | 42 | 0,270 | 2118 | 2147 | 2,661 | 0,753 |
| 5 | 36 | 0,153 | 1199 | 2728 | 2,337 | 0,661 |
| 6 | 30 | 0,077 | 601,96 | 3232 | 1,988 | 0,563 |
| 7 | 24 | 0,032 | 254,83 | 3651 | 1,617 | 0,458 |
| 8 | 18 | 0,011 | 82,72 | 3982 | 1,229 | 0,348 |
| 9 | 12 | 0,00212 | 16,64 | 4222 | 0,827 | 0,234 |
| 10 | 6 | 0,000134 | 1,05 | 4366 | 0,416 | 0,118 |
| 11 | 0 | 0 | 0 | 4415 | 0 | 0 |
2.4 Подставим найденные значения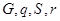 
в уравнение равновесия и определим меридиональное усилие
: 
.
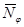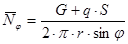2.5 Получим выражение для погонного кольцевого усилия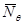 
из уравнения Лапласа при
R 1 = R 2 = R ,
.
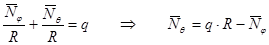Результаты расчёта заносим в таблицу 3 при условии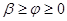 
.
Таблица 3
| № точки | φ, град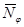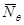. | , Н/м
| ,Н/м
|
| 1 | 60 | 1380 | -1380 |
| 2 | 54 | 1548 | -676,2 |
| 3 | 48 | 1716 | -35,93 |
| 4 | 42 | 1877 | 538,4 |
| 5 | 36 | 2026 | 1,044 |
| 6 | 30 | 2158 | 1477 |
| 7 | 24 | 2272 | 1836 |
| 8 | 18 | 2363 | 2118 |
| 9 | 12 | 2429 | 2320 |
| 10 | 6 | 2470 | 2442 |
| 11 | 0 | 2483 | 2483 |
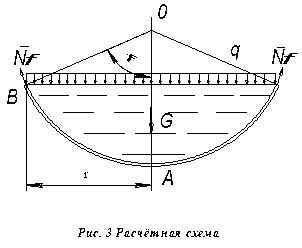
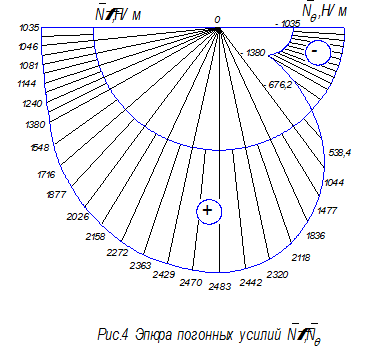
По данным таблиц строим эпюры погонных усилий. Схема эпюры приведена на рис. 4.
С помощью эпюры определяем наиболее напряжённое сечение оболочки и максимальные усилия
.
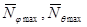Определение толщины стенки оболочки
3.1 Найдём допускаемое напряжение материала оболочки:
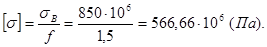
3.2 Определим толщину стенки:
,
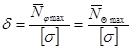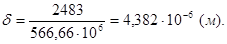
Дата: 2019-05-28, просмотров: 200.
