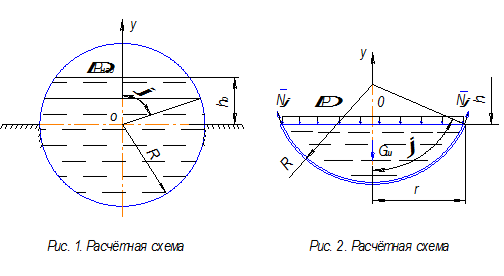
Условие задачи: Сферический топливный бак с опорой по экватору, заполненный жидкостью, находится под давлением наддува (рис.1, рис. 2).
Цель расчёта: Определить толщину стенки и массу конструкции бака при заданных размерах и нагрузке.
Исходные данные:
Радиус оболочки: 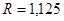 м;
м;
Плотность жидкости (горючее): 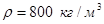 ;
;
Давление наддува: 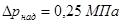 ;
;
Уровень жидкости: 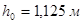 ;
;
Коэффициент осевой перегрузки: 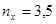 ;
;
Коэффициент безопасности: 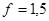 ;
;
Материал оболочки:
марка ВТ6С (О);
предел прочности 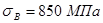 ;
;
плотность 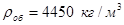 .
.
Примечание: Для упрощения принимаем: 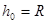 .
.
Выполнение расчёта
Расчёт оболочки над опорой
Формулы для расчёта погонных меридиональных 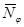 и кольцевых
и кольцевых 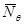 усилий над опорой
усилий над опорой 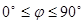 от действия давления жидкости и давления наддува имеют вид:
от действия давления жидкости и давления наддува имеют вид:
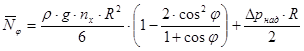 ;
;
 ,
,
где 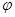 – угол, отсчитываемый в плоскости меридиана от верхнего полюса;
– угол, отсчитываемый в плоскости меридиана от верхнего полюса;
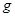 – ускорение свободного падения.
– ускорение свободного падения.
Принимая угол 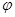 в диапазоне от 0˚ до 90˚, занесём значения кольцевых и меридиональных усилий с шагом угла
в диапазоне от 0˚ до 90˚, занесём значения кольцевых и меридиональных усилий с шагом угла 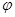 , равным 10˚,в таблицу 1.
, равным 10˚,в таблицу 1.
Таблица 1
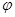 , град , град
| 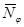 , Н/м , Н/м
|  , Н/м , Н/м
|
| 0 | 140600 | 140600 |
| 10 | 140800 | 141000 |
| 20 | 141100 | 142200 |
| 30 | 141800 | 144100 |
| 40 | 142600 | 146800 |
| 50 | 143500 | 150200 |
| 60 | 144500 | 154100 |
| 70 | 145400 | 158700 |
| 80 | 146100 | 163900 |
| 90 | 146400 | 169600 |
Расчёт оболочки под опорой
Выведем расчётные формулы для погонных меридиональных и кольцевых усилий от действия давления жидкости и давления наддува под опорой топливного бака  . Составим уравнение равновесия внешних и внутренних сил для выделенного сечения оболочки (рис. 2) в проекции на вертикальную ось
. Составим уравнение равновесия внешних и внутренних сил для выделенного сечения оболочки (рис. 2) в проекции на вертикальную ось 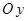 . Получим:
. Получим:
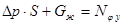 ,
,
где 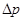 – давление в рассматриваемом сечении; S – площадь расчётного поперечного сечения;
– давление в рассматриваемом сечении; S – площадь расчётного поперечного сечения;
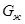 – вес жидкости в шаровом сегменте, отсечённом нормальным коническим сечением с углом
– вес жидкости в шаровом сегменте, отсечённом нормальным коническим сечением с углом 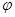 ;
;
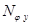 – равнодействующая погонных меридиональных усилий
– равнодействующая погонных меридиональных усилий  в проекции на ось
в проекции на ось 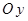 .
.
Давление 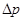 в произвольном сечении оболочки равно давлению наддува плюс давление столба жидкости над рассматриваемым сечением:
в произвольном сечении оболочки равно давлению наддува плюс давление столба жидкости над рассматриваемым сечением:
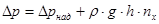 ,
,
где h – высота столба жидкости от зеркала жидкости до расчётного сечения.
 ,
,
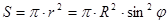 ,
,
где 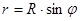 - радиус рассматриваемого сечения.
- радиус рассматриваемого сечения.
Определим вес жидкости в шаровом сегменте: 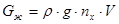 ,
,
где 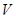 – объём шарового сегмента, отсечённого нормальным коническим сечением с углом
– объём шарового сегмента, отсечённого нормальным коническим сечением с углом 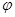 .
.
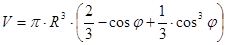 .
.
Спроектируем погонные меридиональные усилия  в расчётном сечении на вертикальную ось
в расчётном сечении на вертикальную ось 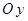 :
: 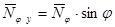 .
.
Величина равнодействующей 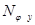 от распределённых по кольцу радиуса r меридиональных сил
от распределённых по кольцу радиуса r меридиональных сил 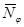 определяется по формуле:
определяется по формуле:
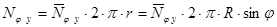 .
.
Окончательно получаем 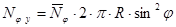 .
.
Принимая угол 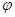 в диапазоне от 90˚ до 0˚, занесём значения составляющих уравнения равновесия с шагом угла
в диапазоне от 90˚ до 0˚, занесём значения составляющих уравнения равновесия с шагом угла 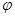 , равным 10˚,в таблицу 2.
, равным 10˚,в таблицу 2.
Таблица 2
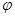 , град , град
| 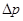 , МПа , МПа
| S, м2 | 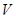 , , 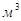
| 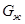 , Н , Н
|
| 90 | 0,2809 | 3,976 | 2,982 | 81910 |
| 80 | 0,2863 | 3,856 | 2,213 | 60790 |
| 70 | 0,2915 | 3,511 | 1,512 | 41530 |
| 60 | 0,2964 | 2,982 | 0,932 | 25600 |
| 50 | 0,3008 | 2,333 | 0,503 | 13810 |
| 40 | 0,3046 | 1,643 | 0,226 | 6201 |
| 30 | 0,3077 | 0,994 | 0,077 | 2107 |
| 20 | 0,3099 | 0,465 | 0,016 | 437,881 |
| 10 | 0,3113 | 0,120 | 0,001027 | 28,215 |
| 0 | 0,3118 | 0 | 0 | 0 |
Подставляем полученные выражения 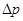 , S,
, S, 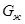 ,
, 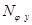 в уравнение равновесия и преобразовываем.
в уравнение равновесия и преобразовываем.
Получаем формулу для вычисления погонных меридиональных усилий:
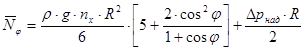 .
.
Подставляя полученное выражение  в уравнение Лапласа, определим погонные кольцевые усилия
в уравнение Лапласа, определим погонные кольцевые усилия 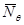 . Уравнения Лапласа в усилиях имеет вид:
. Уравнения Лапласа в усилиях имеет вид:
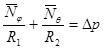 ,
,
где 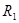 ,
, 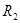 – главные радиусы кривизны оболочки;
– главные радиусы кривизны оболочки; 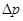 – давление в рассматриваемом сечении.
– давление в рассматриваемом сечении.
Для сферического бака R 1 = R 2 = R, поэтому уравнение Лапласа принимает вид:
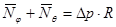 .
.
Подставив выражение 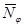 в уравнение Лапласа и проведя преобразования, получим формулу для вычисления
в уравнение Лапласа и проведя преобразования, получим формулу для вычисления 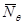 :
:
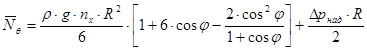 .
.
Принимая угол 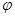 в диапазоне от 90˚ до 0˚, занесём значения составляющих уравнения равновесия с шагом угла
в диапазоне от 90˚ до 0˚, занесём значения составляющих уравнения равновесия с шагом угла 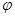 , равным 10˚,в таблицу 3.
, равным 10˚,в таблицу 3.
Таблица 3
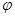 , град , град
| 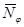 , Н/м , Н/м
|  , Н/м , Н/м
|
| 90 | 169600 | 146400 |
| 80 | 169900 | 152200 |
| 70 | 170600 | 157300 |
| 60 | 171500 | 161900 |
| 50 | 172500 | 165900 |
| 40 | 173400 | 169200 |
| 30 | 174300 | 171900 |
| 20 | 174900 | 173800 |
| 10 | 175300 | 175000 |
| 0 | 175400 | 175400 |
Погонные усилия в сферическом баке принимают наибольшее значение в нижнем полюсе. Кроме того, в нижнем полюсе  =
= 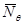 . Сравнивая результаты вычислений значений
. Сравнивая результаты вычислений значений 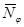 ,
,  на экваторе для участков над опорой и под опорой, делаем вывод: усилия
на экваторе для участков над опорой и под опорой, делаем вывод: усилия  ,
,  терпят разрыв.
терпят разрыв.
Дата: 2019-05-28, просмотров: 356.