Силы инерции определяем по формуле:
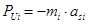(3.11)
где: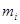 
- масса i-го звена, кг ;
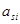- ускорение центра масс i-го звена,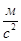 
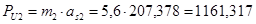
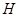
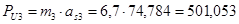
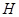
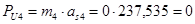
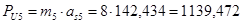
Определяем моменты инерции звеньев:
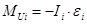(3.12)
где: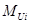 
- момент инерции i-го звена,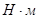 
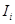- момент инерции i-го звена относительно центра масс,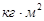 
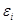- угловая скорость i-го звена,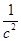 
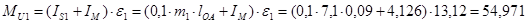
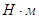
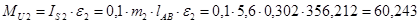
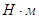
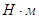
Рассчитаем силу тяжести каждого звена:
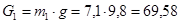
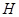
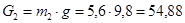
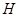
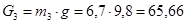
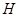
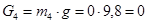
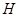
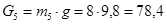
3.4 Определение реакций в кинематических парах и уравновешивающей силы методом планов
Рассмотрим группу Асура 5-0: Сила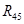 
и 
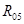найдем из следующего уравнения:
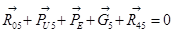
Масштабный коэффициент сил:
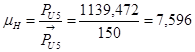
где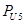 
- алгебраическое значение силы, Н
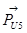длина вектора силы на плане, 
.
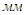Определим длины векторов: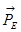 
, 
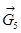
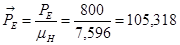
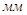
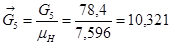
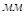
Из плана сил определяем значения неизвестных сил:
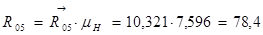
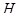
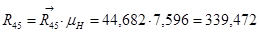
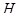
Таблица 3.2 – Силы и вектора сил 4-го звена.
| 
| 
| 
| 
| |
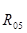
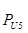
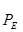
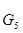
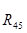
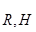
| 78,4 | 1139,472 | 800 | 78,4 | 339,472 |
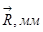
| 10,321 | 150 | 105,318 | 10,321 | 44,691 |
Рассмотрим звено №4 (ползун):
Так как силы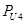 
и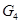 
равны нулю, то на ползун действует только две силы, которые расположены на одной прямой и противоположны по направлению.
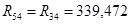
Рассмотрим группу Асура 2-3:
Найдём тангенциальные реакции из следующих уравнений:
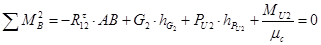(3.13)
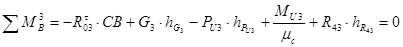(3.14)
Из уравнения (3.13) получим
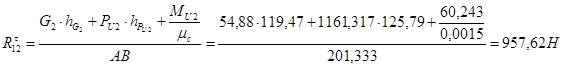
Из уравнения (3.14) получим
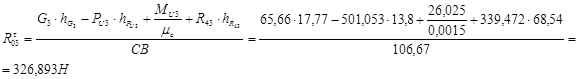
С помощью плана сил определим неизвестные реакци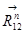и 
и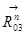 
:
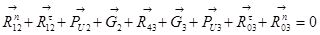
Найдём масштабный коэффициент
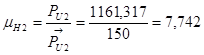
Из плана сил определяем значения неизвестных сил:
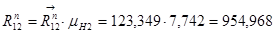
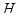
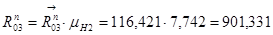
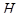
Реакцию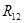 
определяем из следующего векторного уравнения
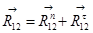
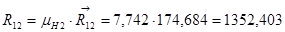
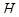
Таблица 3.3 – Силы и вектора сил 2-го и 3-го звеньев.
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
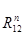
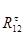
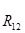
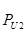
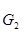
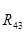
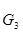
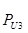
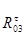
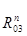
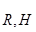
| 954,968 | 957,62 | 1352,403 | 1161,317 | 54,88 | 339,472 | 65,66 | 501,053 | 326,893 | 901,331 |
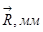
| 123,349 | 123,691 | 174,684 | 150 | 7,089 | 43,848 | 8,481 | 64,719 | 42,223 | 116,421 |
Рассмотрим начальный механизм.
Определим уравновешивающую силу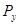 
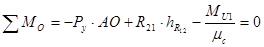
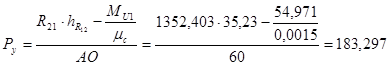
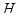
Уравновешивающий момент равен
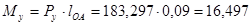
Реакцию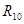 
определяем графически
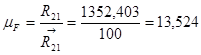
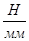
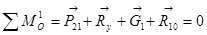
Из плана сил находим
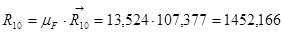
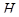
Определение уравновешивающей силы методом Жуковского
Для этого к повёрнутому на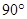 
плану скоростей в соответствующих точках прикладываем все внешние силы действующие на механизм, не изменяя их направления. Моменты раскладываем на пару сил, изменив их направления.
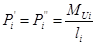, (3.15)
где: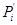 
и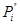 
- пара сил,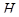
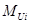- момент инерции i-го звена,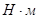 
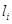- длина i-го звена,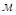 
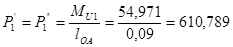
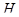
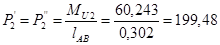
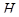
Записываем уравнение моментов сил относительно полюса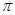 
:
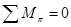, отсюда
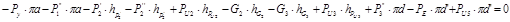
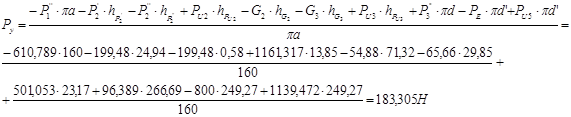
Уравновешивающий момент равен
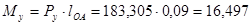
Расчёт погрешности 2-х методов
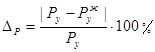, (3.16)
где: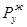 
- сила полученная методом Жуковского,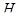 
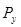- сила полученная методом планов,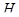 
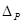- погрешность,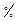 
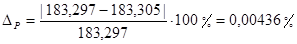
ПРОЕКТИРОВАНИЕ КИНЕМАТИЧЕСКОЙ СХЕМЫ ПЛАНЕТАРНОГО РЕДУТОРА И РАСЧЁТ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ
4.1 подбор числа зубьев и числа сателлитов планетарного редуктора
Рисунок 4.1
Передаточное отношение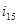 
равно
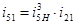(4.1)
где: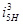 
- передаточное отношение от 5-го звена к водилу, при неподвижном третьем звене
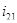- передаточное отношение от 2-го звена к первому
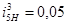из задания
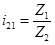(4.2)
где: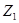 
- число зубьев первого колеса
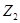- число зубьев второго колеса
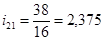
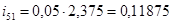
Определим неизвестные числа зубьев колёс:
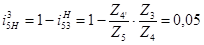
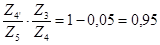
Запишем условие соосности
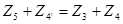(4.3)
Зная передаточное отношение и условие соосности подбираем значения чисел зубьев, которые удовлетворяют этим условиям.
Исходя из предыдущих двух условий, выбираем:
, 
, 
, 
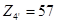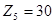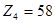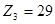
Передаточное отношение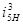 
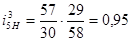- выполняется
Условие соосности
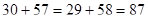- выполняется
Проверяем условие соседства:
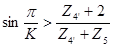(4.4)
где: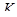 
- число сателлитов планетарного механизма
При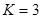 
имеем
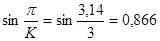
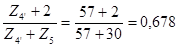
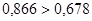- условие соседства выполняется
Проверяем условие сборки
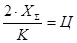(4.5)
где :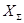 
- сумма чисел зубьев в одной из ступеней механизма
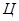- целое число
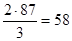- условие сборки выполняется
4.2 Исследование планетарного механизма графическим и аналитическим способом
Рассчитаем радиусы колёс
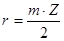(4.6)
где: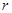 
- радиус колеса, мм
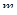- модуль
Дата: 2019-05-28, просмотров: 248.
