На планах скоростей прикладываем все силы, действующие на механизм, и указываем их плечи. Составляем сумму моментов относительно полюса и решаем уравнение.
Для 1-го положения:
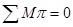
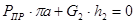 (2.14)
(2.14)
где: 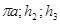 плечи соответствующих сил, снятые с плана скоростей, мм.
плечи соответствующих сил, снятые с плана скоростей, мм.
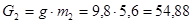 H,
H, 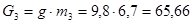 H
H
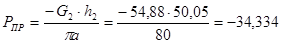 H
H
Находим момент привидения:
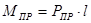 (2.15)
(2.15)
где: 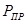 - приведённая сила, Н
- приведённая сила, Н
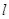 - длина соответствующего звена, м
- длина соответствующего звена, м
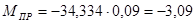 Н∙м
Н∙м
Для 2-го положения:
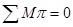
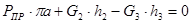
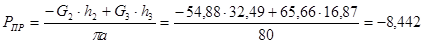 H
H
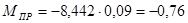 Н∙м
Н∙м
Для 3-го положения:
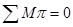
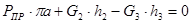
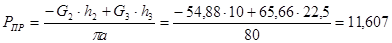 H
H
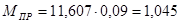 Н∙м
Н∙м
Для 4-го положения:
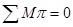
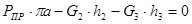
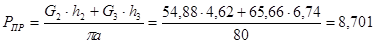 H
H
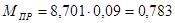 Н∙м
Н∙м
Для 5-го положения:
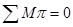
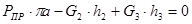
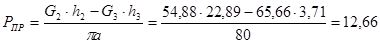 H
H
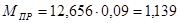 Н∙м
Н∙м
Для 6-го положения:
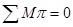
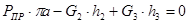
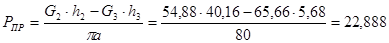 H
H
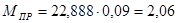 Н∙м
Н∙м
Для 7-го положения:
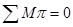
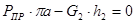
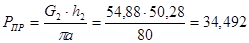 H
H
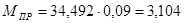 Н∙м
Н∙м
Для 8-го положения:
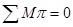
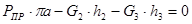
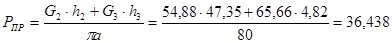 H
H
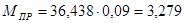 Н∙м
Н∙м
Для 9-го положения:
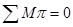
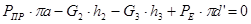
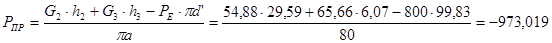 H
H
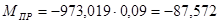 Н∙м
Н∙м
Для 10-го положения:
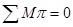
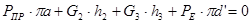
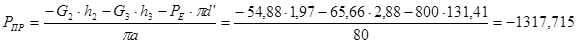 H
H
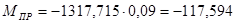 Н∙м
Н∙м
Для 11-го положения:
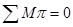
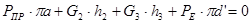
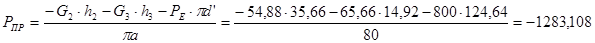 H
H
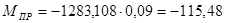 Н∙м
Н∙м
Для 12-го положения:
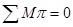
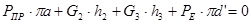
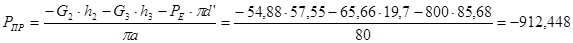 H
H
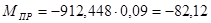 Н∙м
Н∙м
Все значения сводим в таблицу.
Таблица 2.3 – Приведённые моменты сопротивления.
| N положения | 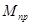 , , 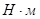
| N положения | 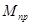 , , 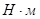
|
| 1 | -3,09 | 7 | 3,104 |
| 2 | -0,76 | 8 | 3,279 |
| 3 | 1,045 | 9 | -87,572 |
| 4 | 0,783 | 10 | -118,594 |
| 5 | 1,139 | 11 | -115,48 |
| 6 | 2,06 | 12 | -82,12 |
Определяем масштабный коэффициент построения графика моментов сопротивления:
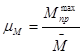 ,
, 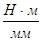 (2.16)
(2.16)
где: 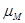 - масштабный коэффициент по оси
- масштабный коэффициент по оси 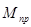
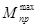 - максимальное значение
- максимальное значение 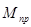 ,
, 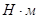
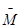 - значение
- значение 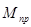 на графике, мм
на графике, мм
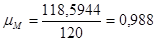
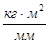
По данным расчёта строится график 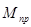 .
.
Путём графического интегрирования графика приведённого момента строится график работ сил сопротивления 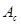 .
.
График работ движущих сил 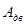 получаем в виде прямой, соединяющей начало и конец графика работ сил сопротивления.
получаем в виде прямой, соединяющей начало и конец графика работ сил сопротивления.
Масштабный коэффициент графика работ:
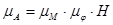 ,
, 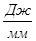 (2.17)
(2.17)
где: Н – полюсное расстояние для графического интегрирования, мм
Н=30мм
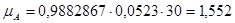
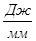
Момент движущий 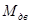 является величиной постоянной и определяется графически.
является величиной постоянной и определяется графически.
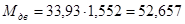
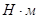
Путём вычитания ординат графика 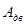 из соответствующих ординат
из соответствующих ординат 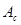 строится график изменения кинетической энергии
строится график изменения кинетической энергии 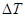 .
.
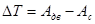 (2.18)
(2.18)
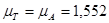
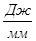
Таблица 2.4 – Значения 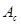 ,
, 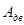 ,
, 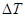
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
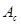 , , 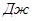
| 0 | -0,39 | -0,26 | 0,08 | 0,38 | 0,98 | 1,78 | 2,8 | 0,93 | -37,84 | -77,52 | -114,68 |
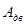 , , 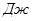
| 0 | -7,34 | -18,65 | -29,96 | -41,27 | -52,58 | -67,2 | -75,36 | -86,67 | -97,98 | -109,29 | -120,6 |
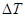 , , 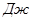
| 0 | -6,95 | -18,39 | -30,04 | -41,65 | -53,56 | -68,98 | -78,16 | -87,6 | -60,14 | -31,77 | -5,92 |
По методу Ф. Витенбауэра на основании ранее построенных графиков 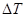 и
и 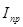 строим диаграмму энергия-масса
строим диаграмму энергия-масса 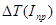 .
.
Определяем углы 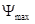 и
и 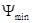 под которыми к диаграмме энергия-масса, проводятся касательные.
под которыми к диаграмме энергия-масса, проводятся касательные.
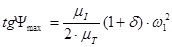 (2.19)
(2.19)
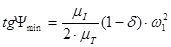 (2.19)
(2.19)
где: 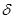 - коэффициент неравномерности вращения кривошипа.
- коэффициент неравномерности вращения кривошипа.
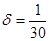
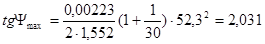
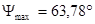
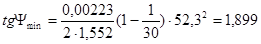
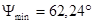
Вследствие того что, пересечение касательных и оси выходит за приделы формата, то ab определим из геометрии с помощью следующей формулы:
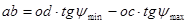 ,мм
,мм
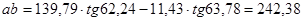 мм
мм
Определяем момент инерции маховика
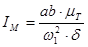 ,
, 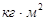 (2.20)
(2.20)
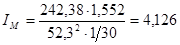
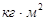
Маховик устанавливается на валу звена приведения.
Определим основные параметры маховика.
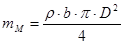 ,кг (2,21)
,кг (2,21)
где: 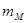 - масса маховика, кг
- масса маховика, кг
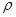 - плотность материала,
- плотность материала, 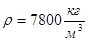 (материал-Сталь 45)
(материал-Сталь 45)
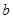 - ширина маховика, м
- ширина маховика, м
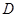 - диаметр маховика, м
- диаметр маховика, м
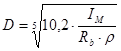 ,м (2,22)
,м (2,22)
где: 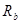 - коэффициент (0,1÷0,3),
- коэффициент (0,1÷0,3), 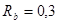
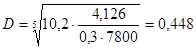 м
м
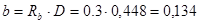 м
м
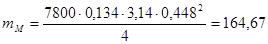 кг
кг
СИЛОВОЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА
3.1 Построение плана скоростей для расчётного положения
Расчётным положением является положение №11. Построение плана скоростей описано в разделе №2. Масштабный коэффициент плана скоростей
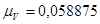
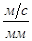
Определение ускорений
Определяем угловое ускорение звена 1.
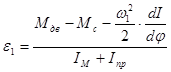 , (3.1)
, (3.1)
где: 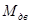 - момент от сил движущих,
- момент от сил движущих, 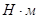
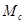 - момент от сил сопротивления,
- момент от сил сопротивления, 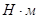
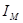 - приведённый момент инерции маховика,
- приведённый момент инерции маховика, 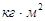
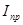 - приведённый момент инерции рычажного механизма для расчётного положения,
- приведённый момент инерции рычажного механизма для расчётного положения, 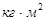
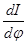 - первая производная от приведённого момента инерции механизма для расчётного положения
- первая производная от приведённого момента инерции механизма для расчётного положения
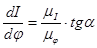 , (3.2)
, (3.2)
где: 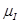 - масштабный коэффициент по оси
- масштабный коэффициент по оси 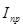 ,
, 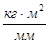
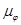 - масштабный коэффициент по оси φ,
- масштабный коэффициент по оси φ, 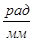
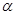 - угол между касательной, проведённой к кривой графика
- угол между касательной, проведённой к кривой графика 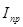 в расчётном положении и осью φ.
в расчётном положении и осью φ. 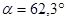
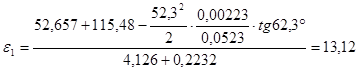
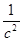
Строим план ускорений для расчётного положения.
Скорость точки А определяем по формуле
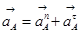 , (3.3)
, (3.3)
где: 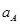 - ускорение точки А,
- ускорение точки А, 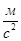
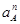 - нормальное ускорение точки А относительно точки О,
- нормальное ускорение точки А относительно точки О, 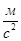
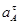 - тангенциальное (касательное) ускорение точки А,
- тангенциальное (касательное) ускорение точки А, 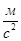
Ускорение  найдём по формуле:
найдём по формуле:
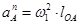 , (3.4)
, (3.4)
где: 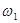 - угловая скорость кривошипа,
- угловая скорость кривошипа, 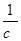
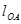 - длина звена ОА, м
- длина звена ОА, м
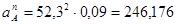
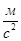
Ускорение 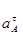 найдём по формуле:
найдём по формуле:
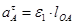 , (3.5)
, (3.5)
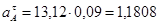
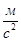
Из произвольно выбранного полюса 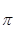 откладываем вектор
откладываем вектор 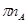 длинной 100мм. Найдём масштабный коэффициент плана скоростей.
длинной 100мм. Найдём масштабный коэффициент плана скоростей.
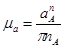 , (3.6)
, (3.6)
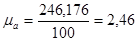
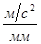
Определим длину вектора 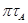 :
:
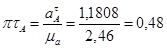
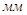
Т.к. 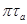 <1мм, то на плане ускорений вектор не строим.
<1мм, то на плане ускорений вектор не строим.
Ускорение точки А определим из следующеё формулы:
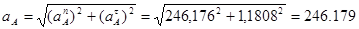
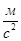
Определим ускорение точки B из следующей системы уравнений:
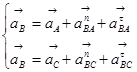 , (3.7)
, (3.7)
Для определения нормальных ускорений точки В относительно точек А и С
Воспользуемся следующими формулами:
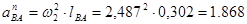
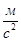
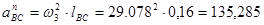
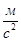
Ускорение точки С равно нулю, т.к. она неподвижна.
Определим длину векторов 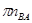 и
и 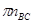 :
:
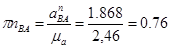
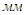
Т.к. 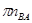 <1мм, то на плане ускорений вектор не строим.
<1мм, то на плане ускорений вектор не строим.
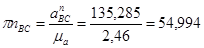
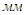
Ускорение точки В найдём, решив системе (3.7) векторным способом:
Из вершины вектора ускорения точки А ( 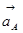 ) откладываем вектор
) откладываем вектор 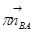 (параллелен звену АВ и направлен от В к А), из вершины вектора
(параллелен звену АВ и направлен от В к А), из вершины вектора 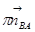 проводим прямую перпендикулярную звену АВ (линия действия
проводим прямую перпендикулярную звену АВ (линия действия 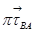 ); из полюса
); из полюса 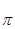 откладываем вектор
откладываем вектор 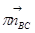 (параллелен звену ВС и направлен от В к С), из вершины вектора
(параллелен звену ВС и направлен от В к С), из вершины вектора 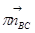 проводим прямую перпендикулярную звену ВС (линия действия
проводим прямую перпендикулярную звену ВС (линия действия 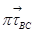 ); на пересечении линий действия векторов
); на пересечении линий действия векторов 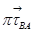 и
и 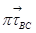 получим точку b, соединив полученную точку с полюсом, получим вектор ускорения точки В. Из плана ускорений определяем вектора тангенциальных ускорений и ускорение точки В:
получим точку b, соединив полученную точку с полюсом, получим вектор ускорения точки В. Из плана ускорений определяем вектора тангенциальных ускорений и ускорение точки В:
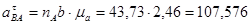
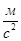
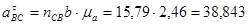
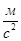
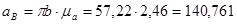
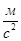
Из полученных тангенциальных ускорений найдём угловые ускорения 2-го и 3-го звеньев:
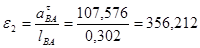
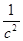
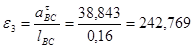
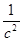
Ускорение точки D найдём из следующего соотношения:
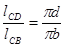 (3.8)
(3.8)
где: 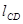 ,
, 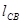 - расстояния между соответствующими точками на механизме, м
- расстояния между соответствующими точками на механизме, м
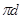 ,
, 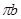 - длинны векторов ускорений на плане, мм
- длинны векторов ускорений на плане, мм
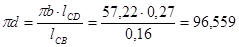 мм
мм
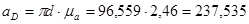
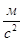
Ускорение точки D’ определим из следующей системы уравнений:
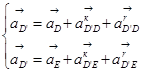 , (3.9)
, (3.9)
где: 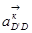 =
= 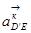 =0, т.к. звенья 4 и 5 не совершают вращательного движения,
=0, т.к. звенья 4 и 5 не совершают вращательного движения,
линия действия 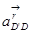 направлена вертикально,
направлена вертикально,
линия действия 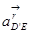 направлена горизонтально.
направлена горизонтально.
Решая систему (3.9) получим 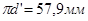 Ускорение точки D’ равно:
Ускорение точки D’ равно:
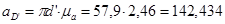
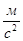
Определим ускорения центров масс звеньев:
Ускорение центра масс 2-го звена 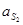 найдём из соотношения (3.10)
найдём из соотношения (3.10)
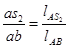 (3.10)
(3.10)
Из плана ускорений 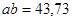 мм
мм
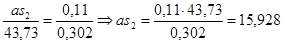 мм
мм
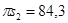 мм
мм
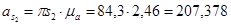
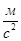
Ускорение центра масс 3-го звена 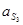 найдём из соотношения (3.11)
найдём из соотношения (3.11)
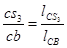 (3.10)
(3.10)
Из плана ускорений 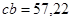 мм
мм
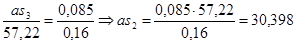 мм
мм
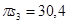 мм
мм
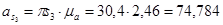
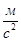
Ускорения центров масс 4-го и 5-го звеньев равны ускорениям точек D и D’ соответственно:
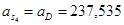
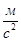
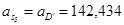
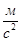
Значения всех ускорений сведём в таблицу:
Таблица З.1 – Ускорения звеньев.
| Ускорение точек механизма | Значение, 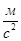
| Ускорение центров масс | Значение, 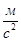
| Угловые ускорения | Значение, 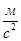
|
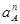
| 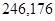
| 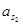
| 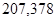
| 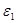
| 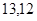
|
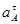
| 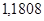
| 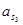
| 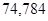
| 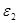
| 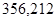
|
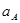
| 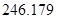
| 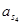
| 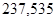
| 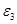
| 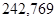
|
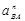
| 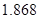
| 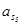
| 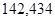
| --- | --- |
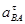
| 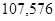
| --- | --- | --- | --- |
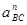
| 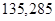
| --- | --- | --- | --- |
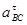
| 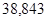
| --- | --- | --- | --- |
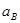
| 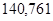
| --- | --- | --- | --- |
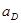
| 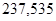
| --- | --- | --- | --- |
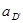
| 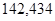
| --- | --- | --- | --- |
Дата: 2019-05-28, просмотров: 292.