Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

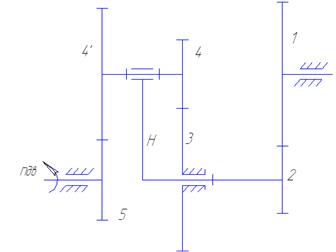
Подвижные звенья механизма.

1 – зубчатое колесо

H – водило

4-4’ – сдвоенный сателлит

5 – центральное колесо

(солнечное)

 

Кинематические пары.

(1-0),вр.,5 кл.

(2-0),вр.,5 кл.

(4-H),вр.,5 кл.

(5-0),вр.,5 кл.

(1-2),вр.,4 кл.

(3-4),вр.,4 кл.

(4‘-5),вр.,4 кл. Рисунок 1.5

 

Найдём число степеней свободы.

Запишем формулу Чебышева.

W=3∙n-2∙P₅-P₄ (1.1)

 

W=3∙4-2∙4-3=1

Число степеней свободы зубчатого механизма равно 1, следовательно, данный механизм является планетарным.

 

Структурный анализ кулачкового механизма

 

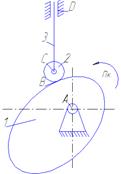Подвижные звенья механизма.

1-кулачок

2-ролик

3-толкатель

 

Кинематические пары.

А (1-0),вр.,5 кл.

В (1-2),4 кл.

С (2-3),вр.,5 кл. Рисунок 1.6

D (3-0),пост.,5 кл.

 

Найдём число степеней свободы.

 

W=3∙n-2∙P₅-P₄

W=3∙3-2∙3-1=2

 

Число степеней свободы равно 2.

 

W≠1 т.к. присутствует лишнее звено ролик.

 

Определим число лишних звеньев по формуле:

 

q=W-W₁ где,

 

q-число лишних звеньев,

W₁-число степеней свободы плоского механизма,

W-имеющееся число степеней свободы.

 

q=2-1=1

 

Для получения W=1 отбросим лишнее звено и рассмотрим новую схему.

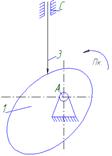
Звенья механизма.

1-кулачок

3-толкатель

Кинематические пары.

А (1-0),вр.,5 кл.

В (1-3),4 кл.

С (0-3),вр.,5 кл. Рисунок 1.7

 

Найдём число степеней свободы.

 

W=3∙n-2∙P₅-P₄

W=3∙3-2∙2-1=1

 

Число степеней свободы кулачкового механизма равно 1.

2. ДИНАМИЧЕСКИЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА

Определение скоростей

 

Для заданной схемы механизма строим 12 положений.

Определяем масштабный коэффициент построения механизма:

 

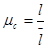 (2.1)

 

где: 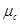 - масштабный коэффициент,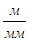

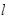 - длина звена,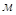

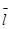 - длина звена на чертеже,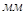

 

 

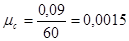
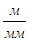
Приступаем к построению повёрнутых планов скоростей для каждого положения. Рассмотрим пример построения для положения №5:

 У кривошипа определяем скорость точки А

 

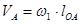 (2.2)

 

где: 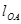 - длина звена,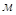

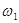 - угловая скорость кривошипа,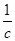

 

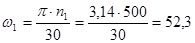
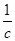
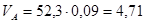
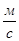
 Для построения вектора скорости точки А определяем масштабный коэффициент

 

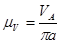 (2.3)

 

где: 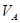 - скорость точки А,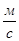

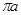 - вектор скорости точки А,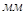

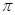 - полюс, выбираемый произвольно

 

 

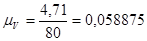
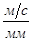
 Для определения скорости точки B запишем систему уравнений:

 

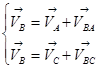 (2.4)

 

Вектор скорости точки А – V_A известен по величине и по направлению. Вектор скорости точки С – V_C равен нулю, т. к. точка С расположена на неподвижной шарнирной опоре. Вектора скорости V_BA и V_BC неизвестны ни по величине, ни по направлению, но нам известны их линии действия, на пересечении которых мы получим точку b. Соединив, полученную точку с полюсом π найдём длину вектора скорости точки B.

 

 

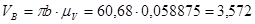
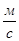
Для определения скорости центра масс 2-го звена S₂ воспользуемся соотношением:

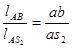 (2.5)

 

где: 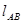, 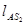- расстояния между соответствующими точками на механизме, м

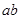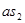,  - длинны векторов скоростей на плане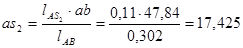, мм

 

 мм

 

Соединив, точку 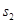 и π получим скорость центра масс второго звена.

 

 

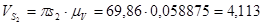
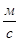
 Для определения скорости точки D воспользуемся следующим соотношением

 

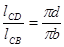 (2.6)

 

где: 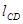, 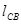- расстояния между соответствующими точками на механизме, м 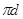,  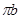- длинны векторов скоростей на плане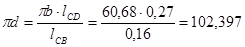, мм

 

 мм

 

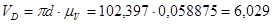
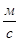
Для определения скорости центра масс 3-го звена S₃ воспользуемся соотношением:

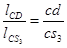 (2.7)

 

где: 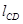, 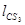- расстояния между соответствующими точками на механизме, м

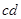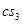,  - длинны векторов скоростей на плане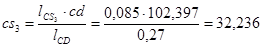, мм

 

 мм

 

т.к. 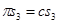, то

 

 

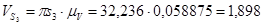
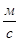
Так как центр массы 4-го звена совпадает точкой D то,

 

 

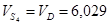
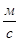
Для определения скорости точки D’ запишем систему уравнений:

 

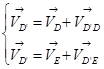 (2.8)

 

Вектор скорости точки D – V_D известен по величине и по направлению. Вектор скорости точки E – V_E равен нулю, т. к. точка E расположена на неподвижной опоре.

Вектора скорости V_D’D и V_D’E неизвестны ни по величине, ни по направлению, но нам известны их линии действия, на пересечении которых мы получим точку d’. Соединив, полученную точку с полюсом π найдём длину вектора скорости точки D’.

 

 

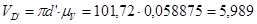
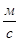
Так как 5-е звено совершает только поступательное движение то, скорости всех точек данного звена одинаковы.

 

 

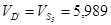
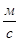
Определим значения угловых скоростей звеньев.

 

 

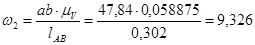
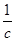
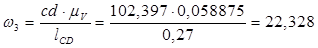
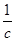
Направление 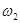 определяем, перенеся вектор ab в точку S₂ – второе звено вращается против часовой стрелки. Аналогично получим, что  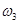направлена по часовой стрелке. Скорости остальных точек определяются аналогичным образом. Все значения сводим в таблицу(2.1).

 

 Таблица 2.1 – Значения линейных и угловых скоростей.

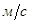
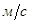
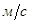
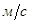
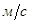
N положения	VB,	VS2,	VD=VS4,	VS3,	VD’=VS5,	VAB,	,	,
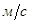
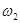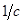
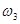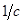
1	0	2,994	0	0	0	4,71	15,596	0
2	2,734	2,933	4,614	1,452	3,367	5,959	19,731	17,089
3	5,335	4,351	9,002	2,834	7,958	4,891	16,194	33,341
4	4,94	4,781	8,337	2,624	8,241	0,767	2,54	30,877
5	3,572	4,113	6,029	1,898	5,989	2,816	9,326	22,328
6	2,166	3,265	3,655	1,151	3,498	4,716	17,177	13,537
7	0	2,994	0	0	0	4,71	15,596	0
8	1,543	3,445	2,604	0,82	2,443	3,659	12,116	9,645
9	3,547	4,237	5,986	1,884	5,877	1,785	5,911	22,17
10	4,596	4,666	7,756	2,441	7,737	0,343	1,135	28,724
11		4,675	7,851	2,472	7,338	0,751	2,487	29,078
12	3,701	4,262	6,246	1,966	5,044	1,999	6,62	23,133