Эксплуатация реальных физических установок обычно требует серьезных финансовых затрат, а к учебным экспериментам на них, к тому же, предъявляются особые требования по технике безопасности. Поэтому для обучения удобно использовать не реальные установки, а их компьютерные модели. Существующие методы, используемые при разработке программ, позволяют существенно приблизить имитационные эксперименты к реальным.

Разработанная компьютерная анимационная обучающая система моделирует в реальном масштабе времени движение тел, масса которых в процессе движения не остается постоянной. Подобные движения широко встречаются в природе и технике. Наибольший интерес рассмотрение движения тел переменной массы приобретает в тех случаях, когда вследствие изменения массы возникают силы, приводящие в движение эти тела. Эти силы, которые получили название реактивных, обеспечивают полет ракет разных систем, реактивных снарядов, самолетов с воздушно - реактивными двигателями и т. п.

Рассмотрим движение тела, масса которого убывает вследствие того, что из него постоянно выбрасываются частицы с некоторой относительной скоростью u.

Введем понятие расход массы 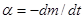 («скоростью убывания массы»).

Изменение импульса системы 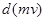 за малый промежуток времени  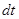на основании второго закона Ньютона можно приравнять импульсу внешних сил :

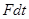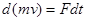
Пусть в момент времени 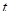 тело имело массу  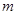и скорость 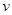; импульс его в этот момент

В момент времени 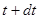 масса этого тела 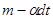, а скорость 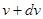; масса выброшенных частиц 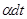, их скорость в той же системе отсчета 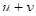. Импульс системы в момент времени  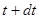будет равен

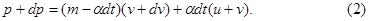
Пренебрегая бесконечно малой величиной второго порядка 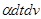, получаем, вычитая (1) из (2),

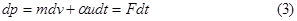
или

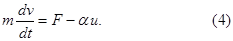
Уравнение (4) представляет собой закон движения тела, выбрасывающего часть своей массы со скоростью 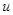 при ежесекундном расходе 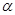. Из этого выражения следует, что в случае движения тела с переменной массой произведение массы движущегося тела на ускорение определяется не только равнодействующей приложенных к ней внешних сил 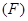, но и реактивной силой, равной произведению расхода массы в секунду  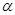на относительную скорость движения отбрасываемых частиц 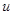. Реактивная сила направлена противоположно скорости, с которой выбрасываемые частицы покидают тело. Уравнение движения тела переменной массы впервые было получено И. В. Мещерским. На основании этого уравнения К. Э. Циолковским впервые были намечены пути решения проблемы космических полетов.

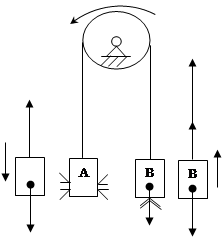
Рис.1

На рис. 1 представлена простейшая механическая модель, позволяющая не только измерить реактивную силу, но и проследить основные закономерности движения тел переменной массы. Основными элементами этой установки являются два цилиндра А и В, соединенные нитью, перекинутой через неподвижный блок С. Цилиндры полые, равного объема и массы. Один из них В имеет одно отверстие в середине дна, другой А – два одинаковых противоположно расположенных отверстия в боковых поверхностях. Оба цилиндра наполняются водой. Отверстия в них выполнены так, что масса воды, вытекающей в единицу времени (расход), одинакова для обоих цилиндров. В результате истечения воды из цилиндра В возникает реактивная сила 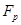, действующая на этот цилиндр и приводящая в движение всю систему. Эта сила направлена вертикально вверх, а величина ее определяется относительной скоростью истечения воды  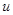и скоростью изменения массы воды в цилиндре:

В предложении, что блок невесом, нить нерастяжима и трение в системе отсутствует, уравнение движения цилиндра В может быть представлено в виде (рис. 1)

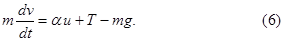
Здесь 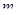 - мгновенное значение массы цилиндра с водой в любой момент времени, Т-упругая сила натяжения нити.

Уравнение движения цилиндра А (при тех же условиях) имеет вид

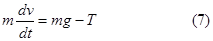
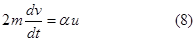
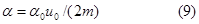
а расстояние 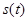, пройденное цилиндром В за время  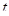, может быть рассчитано по формуле

Где 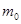-масса цилиндра с водой при .

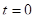ГЛАВА 2. АНИМАЦИОННО – ОБУЧАЮЩИЙ МЕТОД МЕХАНИЧЕСКОЙ СИСТЕМЫ