ГЛАВА1.МЕХАНИЧЕСКИЕ СИСТЕМЫ И АНИМАЦИОННЫЕ МОДЕЛИРОВАНИЕ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Содержание

Введение

Глава 1. Механические системы и анимационное моделирование.

§ 1.1 Некоторые аспекты создания модели механической системы.

§ 1.1.1 Механические системы. Центр масс.

§ 1.1.2 Количество движения системы тел, закон сохранения количества движения

§ 1.1.3 Движение центра масс механической системы.

§ 1.1.4 Движение тел переменной массы. Уравнение Мещерского. Формула Циалковского.

§ 1.2 Некоторые задачи моделирования механических систем (на примере движение тела с переменной массой).

§ 1.3 Анимационное моделирование процесса обучения механических систем.

Глава 2. Анимационно – обучающий метод механической системы.

§ 2.1 Анимация механической системы.

§ 2.1.1 Обучающие программы.

§ 2.1.2 Описание установки.

§ 2.1.3 Алгоритмизация анимационно – обучающей механической системы.

§ 2.2 Инструкция пользования анимационно-обучающей программы “Water Program”

§ 2.3 Текст анимационно – обучающей программы механической системы.

Заключение.

Список использованной литературы.

Введение

При изучения двух тел закон движения одного или двух тел не исчерпывает всех возможных задач о механическом движений с которыми мы сталкиваемся при изучений природы и в технике. Не редко приходиться иметь дело с движением совокупности взаимодействующих между собой тел, или с движением как говорят механической системы. При изучения или обучения таких систем приходиться рассматривать процесс системно. То есть каждую часть этой системы надо представить эту систему в частности и в комплексе учитывая взаимодействие этих систем. Создание физических установок для изучения свойства этих систем является очень сложной задачи. Но с другой стороны с помощью анимационных методов компьютерного моделирования можно создать виртуальной установки свойств механических систем. Такие виртуальные установки при обучения играет не заменимую роль. Так как с помощью этого метода можно полностью не только изучить , но даже визуально представить внутренние движение механической системы. Тем самым можно сказать об актуальности создание таких установок. С другой стороны создание виртуальных установок связанно с созданием концептуальной модели механической системы. Это раз. Второе – алгоритмизации этой модели. Третье – компьютерной реализаций этих алгоритмов. В комплексе решение этих проблем является обязанностью любого информатика.

В принципе создание комплексной модели требует от информатика глубокого знания предложной области. А алгоритмизация выражает способность математическое мышление информатика. В принципе всегда основные анимационные методы заключается – искусственные представление движение в кино, на телевидение или в комплексной графике путем отображения последовательности рисунков или кадров частотой, при которой обеспечивается целостное зрительное восприятие образов. С другой стороны после создания виртуальной анимационной программы установки нам представляет разработки педагогических методов обучения на этой установке. Связи с этим создание анимационной обучающий программы для изучения движения тела с переменной массы является востребованной.

ГЛАВА1.МЕХАНИЧЕСКИЕ СИСТЕМЫ И АНИМАЦИОННЫЕ МОДЕЛИРОВАНИЕ

Некоторые аспекты создания модели механической системы

Центром масс трех материальных точек называется точка, которая делит расстояние между центром масс двух из них и третьей точкой в отношении, обратно пропорциональном сумме масс двух первых и массе третьей из них.

Легко получить координаты центра масс трех материальных точек, подобно тому как это сделано выше для двух точек:

m₂=2

m₁=1

m₃=12

Рис.1. К определению центра масс материальных точек:

-центр масс m₁ и m₂;

- центр масс m₁, m₂и m₃;

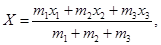
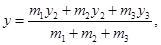
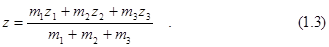
Прибавляя к системе четвертую, пятую и т. д. точки, получим, что координаты центра масс системы n материальных точек:

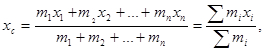
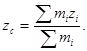
Центр масс механической системы движется так же, как двигалась бы материальная точка, в которой сосредоточена масса всех тел системы, под действием результирующей внешних сил, приложенных к телам, образующим систему.

Если механическая система замкнута, т. е. 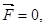то

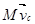=const.

Задачи к главе 1

1.1. Частица движется с импульсом 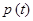под действием силы F(t). Пусть a и b – постоянные векторы, причем a ^ b. Полагая, что:

1) 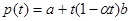, где 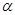- положительная постоянная, найти вектор F в те моменты времени, когда F ^ p;

2) 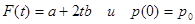, где 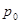- вектор, противоположный по направлению вектору а, найти вектор p в момент 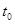, когда он окажется повернутым на 90^○по отношению к вектору .

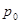Решение. 1. Сила 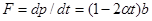, т. е. вектор F все время перпендикулярен вектору a. Следовательно, вектор F будет перпендикулярен вектору p в те моменты, когда коэффициент при b в выражении для 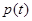обращается в нуль. Отсюда 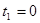и 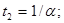соответствующие значения вектора F равны:

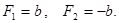
2. Приращение вектора p за промежуток времени 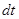есть 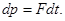Интегрируя это уравнение с учетом начальных условий, находим

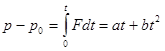
где, по условию, 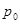противоположен вектору а. Вектор p окажется перпендикулярным вектору 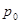в момент 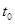, когда 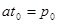. В этот момент .

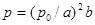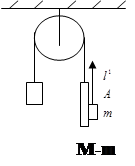Рис. 6

1.2. Через блок (рис. 6) перекинут шнур на одном конце которого находится лестница с человеком А, а на другом – уравновешивающий груз массы М. Человек , масса которого m, совершил вверх перемещение 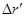относительно лестницы и затем остановился. Пренебрегая массами блока и шнура, а также трением в оси блока, найти перемещение центра инерции этой системы.

Решение. Сначала все тела системы покоились, поэтому приращение импульсов тел при движении равно самим импульсам. Силы натяжения шнура слева и справа одинаковы, а следовательно импульсы груза 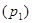и лестницы с человеком 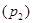в каждый момент времени будут равны между собой, т. т. 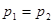, или

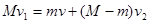где v₁, v и v₂ - - скорости груза, человека и лестницы. Учитывая , что v₂= -v₁ и v=v₂ + v¢, где v¢ - скорость человека относительно лестницы, получим

v₁= (m/2M)v¢. (1)

С другой стороны , импульс всей системы. Отсюда с учетом (1) найдем

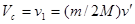И наконец, искомое перемещение

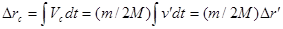Другой способ решения основан на свойстве центра инерции данной системы характеризуется радиусом – вектором

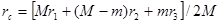где 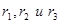- радиусы-векторы центров инерции груза M, лестницы и человека относительно некоторой точки О данной системы отсчета. Отсюда перемещение центра инерции 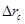равно

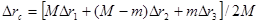где

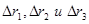-перемещения груза M, лестницы и человека относительно данной системы отсчета. Имея в виду, что 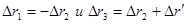получим в результате

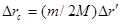1.3. система состоит из двух шариков с массами 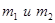, которые соединены между собой невесомой пружинкой. Шарикам сообщили скорости 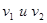, как показано на рис.7, после чего система начала двигаться в однородном поле сил тяжести Земли. Пренебрегая сопротивлением воздуха и считая, что в начальный момент пружинка не деформирована, найти:

1) скорость 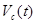центра инерции этой системы в зависимости от времени;

2) внутреннюю механическую энергию системы в процессе движения.

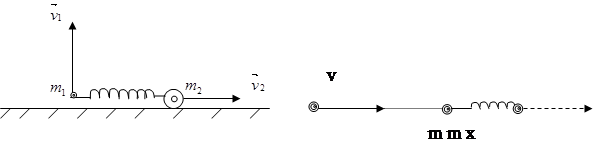Рис. 7 рис. 8

Решение. 1. Приращение вектора скорости центра инерции, есть 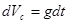. проинтегрировав это уравнение, получим 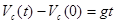, где 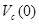-начальная скорость центра инерции. Отсюда

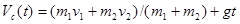3. Внутренняя механическая энергия системы – это ее энергия

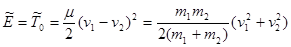4. Шарик с кинетической энергией T, испытав лобовое соударение с первоначально покоившейся упругой гантелью (рис. 8), отлетел в противоположном направлении с кинетической энергией 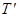. Массы всех трех шариков одинаковы. Найти энергию колебаний гантели после удара.

Решение. пусть 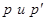-импульсы налетающего шарика до и после удара, а 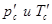-импульс и кинетическая энергия гантели как целого после удара, Е -энергия колебаний. Согласно законам сохранения импульса и энергии,

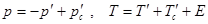Из этих двух уравнений с учетом того, что 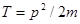, получим

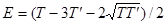5 В К-системе частица 1 массы 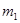налетает на покоящуюся частицу 2 массы 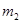. Заряд каждой частицы равен 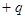. Найти минимальное расстояние, на которое они сблизятся при лобовом соударении, если кинетическая энергия частицы 1 вдали от частицы 2 равна .

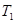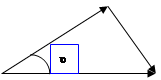
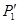
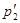
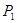
Рис. 9

Решние . Рассмотрим этот процесс как в К-системе, так и в Ц-системе.

1. В К-системе в момент наибольшего сближения обе частицы будут двигаться как единое целое со скоростью 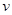, которую можно определить на основании закона сохранения импульса:

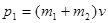где p₁ –импульс налетающей частицы,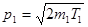

С другой стороны, из закона сохранения энергии следует

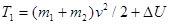где приращение потенциальной энергии системы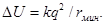

Исключив 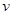из этих двух уравнений, найдем

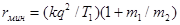2. В Ц-системе решение наиболее просто: здесь суммарная кинетическая энергия частиц идет целиком на приращение потенциальной энергии системы в момент наибольшего сближения:

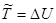где , согласно (4.16),

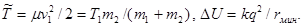
Отсюда легко найти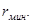

6. Частица массы 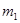с импульсом 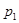испытала упругое столкновение с покоившейся частицей массы 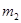. Найти импульс 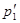первой частицы после столкновения, в результате которого она рассеялась под углом 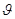к первоначальному направлению движения.

Решение. Из закона сохранения импульса (рис. 69) находим

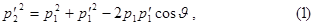
где 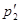-импульс второй частицы после столкновения.

С другой стороны, из закона сохранения энергии следует, что 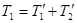, где 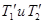-кинетические энергии первой и второй частиц после столкновения. Преобразуем это равенство с помощью соотношения 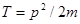к виду

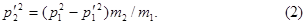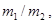Если

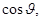
то физический смысл имеет только знак плюс перед корнем. Это следует из того, что при этом условии корень будет больше, чем а так как p^́́’₁– это модуль, то, естественно, он не может быть отрицательным.

Если же m₁>m₂, то физический смысл имеют оба знака перед

корнем – ответ в этом случае получается неоднозначным: под углом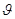

импульс рассеянной частицы может иметь одно из двух значений (это зависит от относительного расположения частиц в момент соударения).

1.7. Какую часть η своей кинетической энергии теряет частица массы m₁ при упругом рассеянии под предельным углом на покоящейся частице массы m₂ , где m₁>m₂

Обучающие программы

Современное время характеризуется возрастающими темпами научно-технического прогресса, непрерывным увеличением объема и изменением содержания знаний, умений и навыков, которыми должны владеть современные специалисты различных категорий, следствием чего является повышение требований к качеству их подготовки.

Одним из перспективных способов повышения эффективности процесса обучения является его автоматизация, т.е. использование в качестве средства обучения современной вычислительной техники. Эффективность использования компьютерной техники зависит от многих факторов. И первым из них следует назвать обучающую программу. Без всякого преувеличения можно утверждать, что она является сердцевиной обучающей системы.

Что представляет собой обучающая программ? Это программа, которая управляет учебной деятельностью учащегося и выполняет, как правило частично, функции учителя. В обучающей программе можно выделить следующие компоненты:

• учебные материалы (тексты, рисунки, схемы, задачи, вопросы и т. д.);

• специальную программу , определяющую, какую именно учебный материал и в какой последовательности представляется учащемуся.

Иногда в обучающей программе содержатся не тексты учебных задач (вопросов), а определенные правила, в соответствии с которыми система генерирует задачи (вопросы). С точки зрения дидактики систему компьютерного обучения можно представить как систему обучающих программ и способов их реализации (иногда вместо термина обучающая программа используют такие термины, как педагогический программный продукт, учебное обеспечение, пакет прикладных программ). Компьютер (техническое обеспечение) и программное обеспечение выступают как средство реализации обучающей программы, а их параметры реализуются с точки зрения возможностей и способов реализации обучающих программ. Это ни в коей мере не снижает роль компьютера и его программного обеспечения. Однако они должны оцениваться не сами по себе, а с точки зрения дидактических возможностей (и, естественно, ограничений), которые оказывают влияние на учебный процесс.

Заключение

Сам процесс изучения физических закономерностей и явлений считается очень сложным. Но с помощью компьютерного моделирования можно разработать хороший метод познания. Такой метод познания осуществляется с помощью анимационо-обучающей программы. Преимущество этого метода при обучении заключаются в следующем:

- Комплексно визуально наблюдать изучаемые физические явления;

- Варирия параметрами моделей, можно вскрыть различные стороны этого явления;

- С помощью обучающих программ можно резко повысить интеллектуальный уровень не только обучающего но и обучаемого;

- Создание таких комплекс программ расширяет программное обеспечение компьютеров;

Список использованной литературы

1. И. Е. Иродов “Основные законы механики” (стр. 120-128)

2. М. М. Архангельский “ Курс физики. Механика ” (стр. 96-109)

3. А. И. Марченко , Л. А. Марченко “Программирование в среде Turbo Pascal”

4. Я.Б.Зельдович “Высшая математика для начинающих” (стр. 383-394)

5. Э.Е. Эвенчик, С.Я.Шамаш, В.А.Орлов. “Методика преподования физики средней школе” (стр.199-205)

Из саитов интернета:

1. www.Bankreferat.ru

2. www.Mail.ru

3. www.Referats.ru

4. www.Aport.ru

5. www.Rambler.ru