Полученный результат может быть распространен на любое число взаимодействующих тел и на силы, меняющиеся со временем. Для этого интервал времени 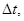 в течение которого происходит взаимодействие тел, разобьем на столь малые промежутки 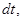в течение каждого из которых силу можно с заданной степенью точности считать постоянной. В течение каждого промежутка времени будет выполняться соотношение (1.8). Следовательно, оно будет справедливо и для всего интервала времени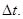  

Для обобщения вывода на 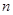 взаимодействующих тел введем понятие замкнутой системы.

Замкнутой называется система тел, для которой результирующая внешних сил равна нулю.

Пусть 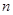 материальных точек массами  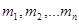образуют замкнутую систему. Изменение количества движения каждой из этих точек в результате взаимодействия ее со всеми остальными точками системы соответственно:

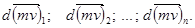
Обозначим внутренние силы, действующие на точку массой 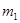 со стороны других точек , через  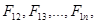на точку массой  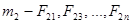и т. д. (Первый индекс обозначает точку, на которую действует сила; второй индекс указывает точку, ос стороны которой действует сила. )

Запишем в принятых обозначениях второй закон динамики для каждой точки в отдельности:

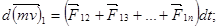
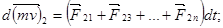
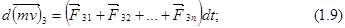
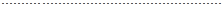
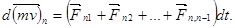
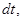Число уравнений равно числу  тел системы. Чтобы найти общее изменение количества движения системы, нужно подсчитать геометрическую сумму изменений количества движения всех точек системы. Просуммировав равенства (1.9), мы получим в левой части полный вектор изменения количества движения системы за время,  а в правой части – элементарный импульс результирующей всех сил, действующих в системе. Но так как система замкнута, то результирующая сил равна нулю. В самом деле, по третьему закону динамики каждой силе  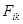в равенствах (1.9) соответствует сила  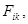причем

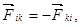 т. е. 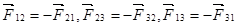 и т. д.,

и результирующая этих сил равна нулю. Следовательно, во всей замкнутой системе изменение количества движения равно нулю:

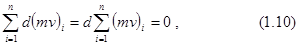
или

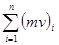=const. (1.11)

полное количество движения замкнутой системы – величина постоянная во все время движения (закон сохранения количества движения).

Закон сохранения количества движения – один из фундаментальных законов физики, справедливый как для систем макроскопических тел, так и для систем, образованных микроскопическими телами: молекулами, атомами и т. п.

Если на точки системы действуют внешние силы, то количество движения, которым обладает система, изменяется.

Напишем уравнения (1.9), включив в них результирующие внешних сил 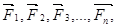 действующих соответственно на первую, вторую и т. д. До 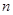-й точки:

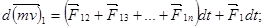
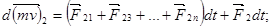
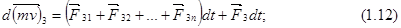
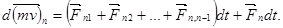
Сложив левые и правые части уравнений, мы получим: слева – полный вектор изменения количества движения системы; справа – импульс результирующей внешних сил:

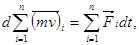
или, обозначая результирующую внешних сил :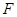

т. е.