В природе и современной технике мы нередко сталкиваемся с движением тел, масса которых меняется со временем. Масса земли возрастет вследствие падения на нее метеоритов, масса метеорита при полете в атмосфере уменьшается в результате отрыва или сгорания его частиц, масса дрейфующей льдины возрастет при намерзании и убывает при таянии и т. д. Движение якоря с якорной цепью, когда все большее число звеньев цепи сходит с лебедки, -пример движения тела переменной массы. Ракеты все систем, реактивные самолеты, реактивные снаряды и мины также являются телами, масса которых изменяется во время движения.
Общие законы динамики тел с переменной массой были открыты и исследованы И. В. Мещерским и К. Э. Циолковским. Циолковским были разработаны фундаментальные проблемы реактивной техники, которые в наши дни служат основной для штурма человеком межпланетных пространств.
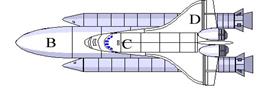
Для вывода основного уравнения движения тела переменной массы рассмотрим конкретный случай движения простейшей ракеты (рис. 4).
Мы будем рассматривать ракету достаточно малое тело, положение центра тяжести которого не меняется по мере сгорания пороха. В этом случае мы можем считать ракету материальной точкой переменной массы, совпадающей с центром тяжести ракеты.
 |
Не рассматривая физико-химическую природу сил, возникающих при отбрасывании от ракеты газов, образованных при сгорании пороха, сделаем такое упрощающее вывод предположение.
Рис.4. Схема порохового снаряда: А-вырывается; В - граната с взрывателем; С – пороховая ракетная камера; D - стабилизатор.
Будем считать , что отбрасываемая от ракеты частица газа dM взаимодействует с ракетой M только в момент их непосредственного контакта. Как только частица dM приобретает скорость относительно точки M, ее воздействие на нее прекращается. Предположим далее, что изменение массы ракеты M происходит непрерывно, без скачков. (Это значит, что мы не рассматриваем многоступенчатые ракеты, масса которых меняется скачкообразно. ) Это предположение позволяет считать, что существует производная от массы по времени.
Пусть в момент t масса ракеты M, а ее скорость относительно неподвижной системы координат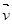 
(рис. 5). Положим, за время dt от ракеты отделилась частица массы (-dM) со скоростью (относительно той же неподвижной системы координат ), равной 
.
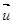Знак «минус» перед приращением массы указывает на то, что приращение это отрицательное, масса ракеты убывает.
Положим, равнодействующая внешних сил, действующих на ракету (силы тяжести и сопротивления среды), F. Как сказано выше, в момент отделения частицы массы (-dM) между ней и ракетой действует неизвестная нам реактивная сила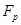 
. Сила 
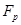для системы ракета – частица является внутренней. Чтобы исключить
 |
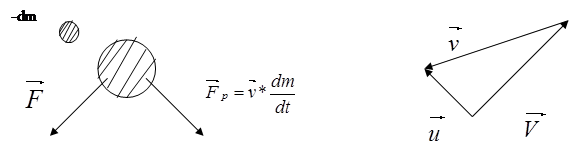Рис.5.К выводу уравнения движения тела переменной массы.
ее из смотрения, вспользуеамя законом изменения количества движения. Количество движения системы ракета – частица а момент t, т. е. перед отделением частицы:
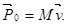
Количество движения системы в момент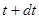 
(после отделения частицы) складывается из количества движения массы 
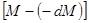, получившей скорость 
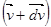, и количества движения массы частицы – dM, летящей со скоростью 
:
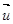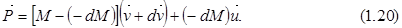
Изменение количества движения системы за время dt:
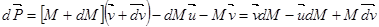
(мы отбросили член второго порядка малости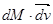 
). Величина 
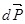должна 
быть приравнена импульсу равнодействующей внешних сил:
Отсюда, перегруппировав члены и разделив на dt, получим основное уравнение движения точки переменной массы:
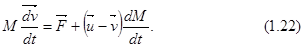
Это уравнение иначе называют уравнением Мещерского. Для ракеты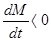 
, так как при полете масса ее убывает. Если масса тела во время движения увеличивается, то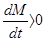 
. При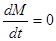 
уравнение (1.22) переходит в уравнение второго закона Ньютона для случая постоянной массы. Величина 
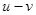есть скорость выбрасываемых ракетой частиц относительно системы координат, движущейся с ракетой. Эту скорость называют обычно просто относительной скоростью V. Тогда равенство (1.22) запишется в виде
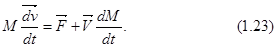
Второй член правой части равенства (1.23) представляет собой реактивную силу, действующую на массу M со стороны вылетевшей частицы dM.
Для любого момента времени произведение массы тела на его ускорение равно векторной сумме равнодействующей приложенных к телу внешних сил и реактивной силы. При движении ракеты вблизи Земли равнодействующая внешних сил представляет собой сумму силы тяжести и силы сопротивления воздуха. Ускорение ракеты зависит еще и от реактивной силы, изменяя величину и направление которой можно управлять полетом ракеты.
Если относительная скорость отбрасываемых частиц равна нулю: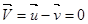 
,то из формулы(1.22) следует:
т. е. если относительная скорость отбрасываемых частиц равна нулю, то уравнение движения точки переменной массы имеет формально тот же вид, что и для точки постоянной массы, но в этом случае масса M- функция времени t.
Важный вклад в механику тел переменной массы применительно к конкретным задачам реактивной техники внесен знаменитым русским ученым Константином Эдуардовичем Циолковским. В 1903 г. была издана его работа «Исследование мировых пространств реактивными приборами», в которой К. Э. Циолковский исследовал ряд случаев прямолинейных движений ракет. К. Э. Циолковским обоснована и доказана возможность практического использования реактивного движения. Им найдены условия, при которых можно получить скорости, достаточные для осуществления космического полета. Полученная им формула, связывающая скорость ракеты с ее начальной массой, до сих пор используется для предварительных расчетов. В работах 1911-1914 гг. он изучил вопрос о величине запасов топлива, необходимых для преодоления сил тяготения Земли, и предложил высококалорийное топливо, позволяющее получить большие скорости истечения газовых струй. К. Э. Циолковского по праву считают изобретателем жидкостных ракет дальнего действия и основоположником теории межпланетных полетов.
Ему принадлежит идея разработки теории так называемых многоступенчатых ракет, когда на некоторых интервалах времени масса ракеты меняется непрерывно, а в некоторые моменты – скачком. Им проведены большие исследования по оценке сил сопротивления при движении тел переменной массы. К. Э. Циолковским поставлен целый ряд оригинальных проблем, имеющих решающее значение для развития реактивной техники.
Для того чтобы выяснить основные факторы, создающие возможность реактивного движения с большими скоростями, рассмотрим движение точки переменной массы безвоздушном пространстве (отсутствует сопротивление движению тела), без действия внешних сил (силы тяготения) . предположим, что скорость истечения частиц направлена прямо противоположно вектору скорости тела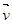 
. Эти условия соответствуют так называемой первой задаче Циолковского. В результате получаем формулу Циолковского и следствие из нее. Найдем при сделанных предположениях скорость движения тела (точки) и закон ее движения.
При сформулированных условиях уравнение движения приобретает вид:
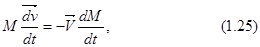
или
Положим,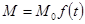 
, где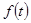 
- функция, определяющая закон изменения массы. Очевидно, так как начальная масса 
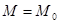, то функция 
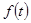при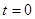 
должна быть 
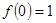. Подставив в (1.26) значение M и проинтегрировав, получим:
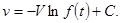
Для определения постоянной С учетом, что при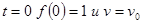 
, тогда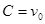 
и
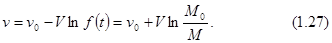
Эта формула носит название формулы Циолковского. Из формулы следует, что скорость, приобретенная точкой переменной массы, зависит от относительной скорости V и отношения начальной массы к остающейся к концу процесса горения. Если масса точки в конце процесса горения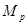 
, отброшенная масса (масса топлива) – m, то при нулевой начальной скорости ( 
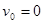) получаем для расчета скорости 
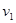в конце процесса горения выражения: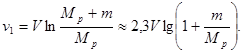 
Отношение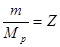 
называют число Циолковского. Для современных ракет можно положить 
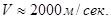. Тогда при числе Циолковского Z=0,250; 9,000; 32,333; 999,000 получим соответственно скорости 
.
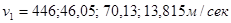Из формулы Циолковского (1.27) следует , что:
1) Скорость точки переменной массы в конце активного участка (в конце процесса отбрасывания частиц) тем больше, чем больше скорость отбрасывания частиц;
2) Скорость в конце активного участка тем больше, чем больше число Циолковского;
3) Скорость точки переменной массы в конце активного участка не зависит от закона изменения массы (режима горения). Заданному числу Циолковского соответствует определенная скорость точки в конце процесса горения не зависимо от того, быстро или медленно шло горения. Это следствие является проявлением закона сохранения количества движения;
4) Для получения возможно больших скоростей точки переменной массы в конце активного участка выгоднее идти по пути увеличения относительной скорости отбрасывания частиц, чем по пути увеличения запасов топлива.
§1.2 Некоторые задачи моделирования механических систем (на примере движение тела с переменной массой)
Имеется много случаев, когда масса тела изменяется в процессе движения за счет непрерывного отделения или присоединения вещества (ракета, реактивный самолет, платформа, нагружаемая на ходу, и др.).
Наша задача: найти уравнение движения такого тела.
Рассмотрим решение этого вопроса для материальной точки, называя ее для краткости телом. Пусть в некоторой момент времени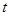 
масса движущего тела A равна m, а присоединяемая (или отделяемая) масса имеет скорость u относительно данного тела.
Введем вспомогательную инерциальную K-систему отсчета, скорость которой такова же, как и скорость тела A в данный момент 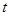. Это значит, что а момент 
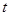тело A покоится в K- системе.
Пусть далее за промежуток времени от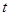 
до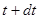 
тело A приобретает в K-системе импульс 
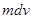. Этот импульс тело A получит, во-первых, вследствие присоединения (отделения) массы 
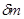, которая приносит (уносит) импульс 
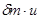, и, во-вторых, вследствие действия силы F со стороны окружающих тел или силового поля. Таким образом, можно записать , что
,
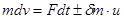где знак плюс соответствует присоединению массы, а знак минус – отделению. Оба эти случая можно объединить, представив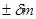 
в виде приращения 
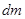массы тела A (действительно, в случае присоединения массы 
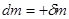, а в случае отделения 
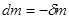). Тогда предыдущее уравнение примет вид
.
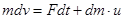Поделив это выражение на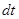 
, получим
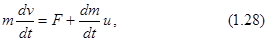
где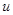 
- скорость присоединяемого (или отделяемого) вещества относительно рассматриваемого тела.
Это уравнение является основным уравнением динамики материальной точки с переменной массой. Его называют уравнением Мещерского. Будучи полученным в одной инерциальной системе отсчета, это уравнение в силу принципа относительности справедливо и в любой другой инерциальной системе. Заметим , что если система отсчета неинерциальная, то под силой F следует понимать результирующую как сил взаимодействия данного тела с окружающими телами, так и сил инерции.
Последний член уравнения (1.26) носит название реактивной силы: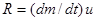 
. Эта сила возникает в результате действия на данное тело присоединяемой (или отделяемой) массы. Если масса присоединяется, то 
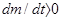и вектор R совпадает по направлению с вектором u; если же масса отделяется, то 
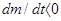и вектор R противоположен вектору u.
Уравнение Мещерского по своей форме совпадает с основным уравнением динамики материальной точки постоянной массы: слева – произведение массы тела на ускорение, справа – действующие на него силы, включая реактивную силу. Однако в случае переменной массы нельзя внести массу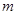 
под знак дифференцирования и представить левую часть уравнения как производную по времени от импульса, ибо 
,
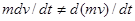Обратим внимание на два частных случая.
1. Если u=0. т. е. масса присоединяется или отделяется без скорости относительно тела, то R=0, и уравнение (1.26) принимает вид
где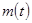 
- масса тела в данный момент времени. Это уравнение определяет , например, движение платформы, из которой свободно высыпается песок (см. задачу 10, пункт 1-й).
2. Если u=-v, т. е. присоединяемая масса неподвижна в выбранной системе отсчета или отделяемая масса становится неподвижной в этой системе, то уравнение (1.28) принимает другой вид
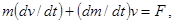
или
иначе говоря, в этом частном случае – и только этом – действие силы F определяет изменение импульса тела с переменной массой. Данный случай реализуется, например, при движении платформы, нагружаемой сыпучим веществом из неподвижного бункера (см. задачу 10, пункт 2-й).
Рассмотрим пример на применение уравнения Мещерского.
Пример. Ракета движется в инерциальной K-системе отсчета в отсутствие внешнего силового поля, причем так, что газовая струя вылетает с постоянной относительно ракеты скоростью u. Найти зависимость скорости ракеты от ее массы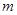 
, если в момент старта ее масса была равна 
.
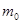В данном случае F=0 и из уравнения (1.28) следует
.
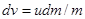Проинтегрировав это выражение с учетом начальных условий, получим
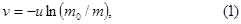
где знак минус показывает, что вектор v (скорость ракеты) противоположен по направлению вектору u. Отсюда видно, что скорость ракеты в данном случае (u=const) не зависит от времени сгорания топлива: v определяется только отношением начальной массы 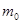ракеты к оставшейся массе m.
Заметим, что если бы вся масса горючего была одновременно выброшена со скоростью u относительно ракеты , то скоростью последней оказалась бы иной. Действительно, если ракета вначале покоилась в выбранной инерциальной системе отсчета, а после одновременного выброса всего горючего приобрела скорость v, то из закона сохранения импульса для системы ракета – горючее следует
,
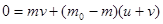где u+v - скорость горючего относительно данной системы отсчета. Отсюда
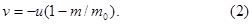
скорость ракеты v в этом случае оказывается меньше, чем в предыдущем (при одинаковых значениях отношения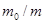 
). В этом нетрудно убедиться, сравнив характер зависимости v от 
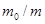в обоих случаях. С ростом 
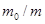в первом случае (когда вещество отделяется непрерывно) скорость v ракеты, согласно (1), растет неограниченно, во втором же (когда вещество отделяется одновременно) скорость v, согласно (2), стремится к пределу, равному - u.
Задачи к главе 1
1.1. Частица движется с импульсом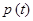 
под действием силы F(t). Пусть a и b – постоянные векторы, причем a ^ b. Полагая, что:
1) 
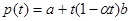, где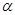 
- положительная постоянная, найти вектор F в те моменты времени, когда F ^ p;
2) 
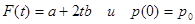, где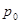 
- вектор, противоположный по направлению вектору а, найти вектор p в момент 
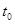, когда он окажется повернутым на 90○ по отношению к вектору .
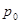Решение. 1. Сила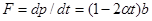 
, т. е. вектор F все время перпендикулярен вектору a. Следовательно, вектор F будет перпендикулярен вектору p в те моменты, когда коэффициент при b в выражении для 
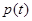обращается в нуль. Отсюда 
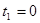и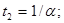 
соответствующие значения вектора F равны:
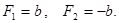
2. Приращение вектора p за промежуток времени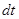 
есть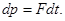 
Интегрируя это уравнение с учетом начальных условий, находим
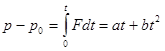
где, по условию,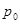 
противоположен вектору а. Вектор p окажется перпендикулярным вектору 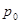в момент 
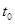, когда 
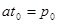. В этот момент 
.
 |
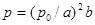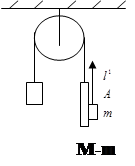Рис. 6
1.2. Через блок (рис. 6) перекинут шнур на одном конце которого находится лестница с человеком А, а на другом – уравновешивающий груз массы М. Человек , масса которого m, совершил вверх перемещение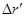 
относительно лестницы и затем остановился. Пренебрегая массами блока и шнура, а также трением в оси блока, найти перемещение центра инерции этой системы.
Решение. Сначала все тела системы покоились, поэтому приращение импульсов тел при движении равно самим импульсам. Силы натяжения шнура слева и справа одинаковы, а следовательно импульсы груза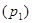 
и лестницы с человеком 
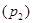в каждый момент времени будут равны между собой, т. т. 
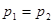, или
,
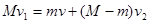где v1, v и v2 - - скорости груза, человека и лестницы. Учитывая , что v2= -v1 и v=v2 + v¢, где v¢ - скорость человека относительно лестницы, получим
v1= (m/2M)v¢. (1)
С другой стороны , импульс всей системы. Отсюда с учетом (1) найдем
.
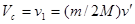И наконец, искомое перемещение
.
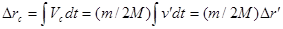Другой способ решения основан на свойстве центра инерции данной системы характеризуется радиусом – вектором
,
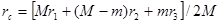где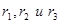 
- радиусы-векторы центров инерции груза M, лестницы и человека относительно некоторой точки О данной системы отсчета. Отсюда перемещение центра инерции 
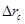равно
,
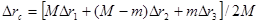где
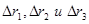-перемещения груза M, лестницы и человека относительно данной системы отсчета. Имея в виду, что 
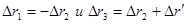получим в результате
.
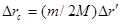1.3. система состоит из двух шариков с массами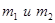 
, которые соединены между собой невесомой пружинкой. Шарикам сообщили скорости 
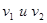, как показано на рис.7, после чего система начала двигаться в однородном поле сил тяжести Земли. Пренебрегая сопротивлением воздуха и считая, что в начальный момент пружинка не деформирована, найти:
1) скорость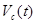 
центра инерции этой системы в зависимости от времени;
2) внутреннюю механическую энергию системы в процессе движения.
 |
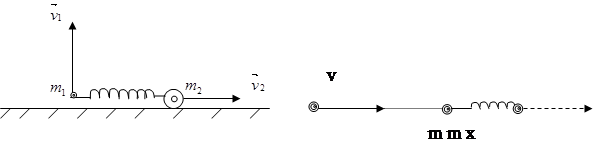Рис. 7 рис. 8
Решение. 1. Приращение вектора скорости центра инерции, есть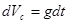 
. проинтегрировав это уравнение, получим 
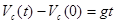, где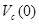 
-начальная скорость центра инерции. Отсюда
.
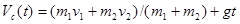3. Внутренняя механическая энергия системы – это ее энергия
.
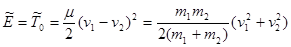4. Шарик с кинетической энергией T, испытав лобовое соударение с первоначально покоившейся упругой гантелью (рис. 8), отлетел в противоположном направлении с кинетической энергией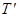 
. Массы всех трех шариков одинаковы. Найти энергию колебаний гантели после удара.
Решение. пусть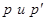 
-импульсы налетающего шарика до и после удара, а 
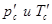-импульс и кинетическая энергия гантели как целого после удара, Е -энергия колебаний. Согласно законам сохранения импульса и энергии,
.
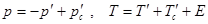Из этих двух уравнений с учетом того, что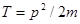 
, получим
.
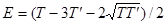5 В К-системе частица 1 массы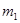 
налетает на покоящуюся частицу 2 массы 
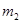. Заряд каждой частицы равен 
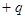. Найти минимальное расстояние, на которое они сблизятся при лобовом соударении, если кинетическая энергия частицы 1 вдали от частицы 2 равна 
.
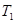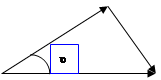
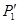
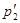
Рис. 9
Решние . Рассмотрим этот процесс как в К-системе, так и в Ц-системе.
1. В К-системе в момент наибольшего сближения обе частицы будут двигаться как единое целое со скоростью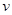 
, которую можно определить на основании закона сохранения импульса:
,
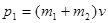где p1 –импульс налетающей частицы,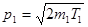 
С другой стороны, из закона сохранения энергии следует
,
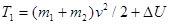где приращение потенциальной энергии системы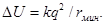 
Исключив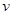 
из этих двух уравнений, найдем
.
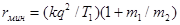2. В Ц-системе решение наиболее просто: здесь суммарная кинетическая энергия частиц идет целиком на приращение потенциальной энергии системы в момент наибольшего сближения:
,
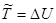где , согласно (4.16),
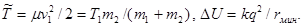
Отсюда легко найти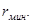 
6. Частица массы 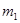с импульсом 
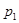испытала упругое столкновение с покоившейся частицей массы 
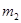. Найти импульс 
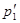первой частицы после столкновения, в результате которого она рассеялась под углом 
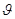к первоначальному направлению движения.
Решение. Из закона сохранения импульса (рис. 69) находим
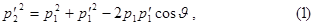
где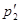 
-импульс второй частицы после столкновения.
С другой стороны, из закона сохранения энергии следует, что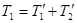 
, где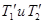 
-кинетические энергии первой и второй частиц после столкновения. Преобразуем это равенство с помощью соотношения 
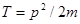к виду
 |
 |
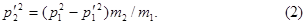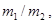Если
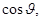
то физический смысл имеет только знак плюс перед корнем. Это следует из того, что при этом условии корень будет больше, чем а так как ṕ́’1 – это модуль, то, естественно, он не может быть отрицательным.
Если же m1>m2 , то физический смысл имеют оба знака перед
корнем – ответ в этом случае получается неоднозначным: под углом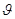 
импульс рассеянной частицы может иметь одно из двух значений (это зависит от относительного расположения частиц в момент соударения).
1.7. Какую часть η своей кинетической энергии теряет частица массы m1 при упругом рассеянии под предельным углом на покоящейся частице массы m2 , где m1>m2
Дата: 2019-05-28, просмотров: 189.
