ex, x0=0
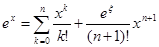 ,x Î (0,x),
,x Î (0,x),
если x>0 или x Î (x,0) в случае x <0.
Например, при |x|<1, |Rn (x) | £ 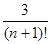
sin x, x0=0
Вспомогательная формула:
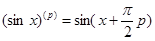
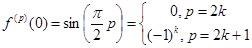
sin x = 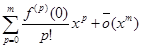 =
= 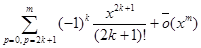 , x ®0,
, x ®0,
выберем m=2n+2, тогда
sin x= 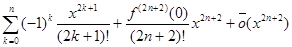 , x ®0,
, x ®0,
откуда, с учетом равенства f (2n+2) (0) =0, получаем разложение для синуса
sin x= 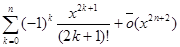 , x ®0
, x ®0
В формуле Тейлора с остатком Лагранжа
sin x = 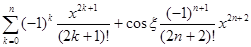 , x Î (0,x) (или x Î (x,0)).
, x Î (0,x) (или x Î (x,0)).
Действительно,
sin x =
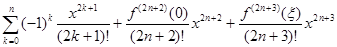 =
= 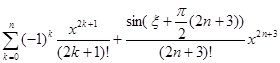 =
= 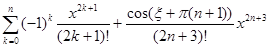 =
= 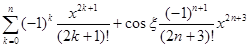 .
.
Откуда следует, что
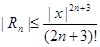
cos x, x0=0
Вспомогательная формула:
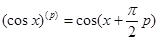
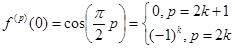
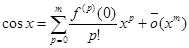 =
= 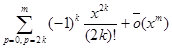 , x ®0,
, x ®0,
выберем m=2n+1, тогда
cos x= 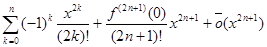 , x ®0,
, x ®0,
откуда, с учетом равенства f (2n+1) (0) =0, получаем разложение для косинуса
cos x= 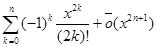 , x ®0
, x ®0
В формуле Тейлора с остатком Лагранжа
cos x = 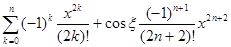 , x Î (0,x) (или x Î (x,0)).
, x Î (0,x) (или x Î (x,0)).
Действительно,
cos x =
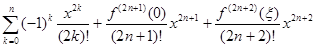 =
= 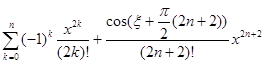 =
= 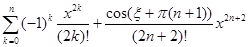 =
= 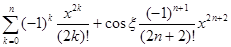 .
.
Откуда следует, что
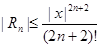
ln (1+x), x0=0
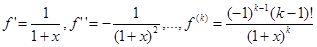
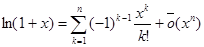 , x ®0
, x ®0
(1+x) a, x0=0,
интерес представляет случай, когда a не является натуральным числом.
f ¢= a (1+x) a-1,…,f (k) = a ( a - 1) … ( a - k+1) (1+x) a - k
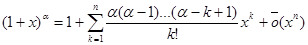 , x ®0
, x ®0
Важный частный случай
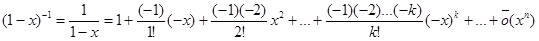 =
= 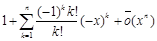 =
= 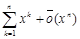 .
.
Примеры использования стандартных разложений для представления функций по формуле Тейлора и для вычисления пределов
Из формул Тейлора следуют известные "равносильности при 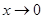 "; например,
"; например,
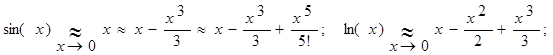
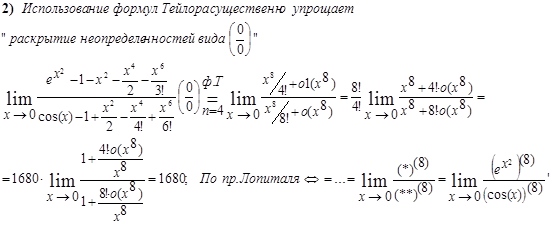
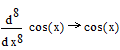

Пример 1.
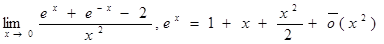
Пример 2.
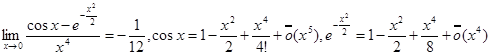 .
.
Пример 3. Разложить функцию f (x) = 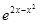 по формуле Тейлора с остатком Пиано по степеням x до x5 включительно.
по формуле Тейлора с остатком Пиано по степеням x до x5 включительно.
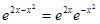 . Для решения задачи возьмем разложения функции
. Для решения задачи возьмем разложения функции
e2x = 1+2x+ 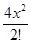 +
+ 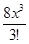 +
+ 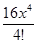 +
+ 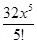 +o (x5),
+o (x5),
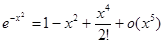
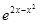 = (1+2x+
= (1+2x+ 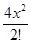 +
+ 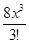 +
+ 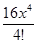 +
+ 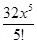 +o (x5)) (
+o (x5)) ( 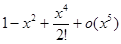 ) =
) =
1+2x+ 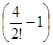 x2+
x2+ 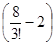 x3+
x3+ 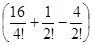 x4+
x4+ 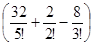 x5+o (x5) =
x5+o (x5) =
1+2 x+ x2 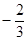 x3
x3 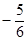 x4
x4 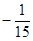 x5+ o ( x5).
x5+ o ( x5).
Пример 4. Разложить функцию f (x) =1/cos x по формуле Тейлора с остатком Пиано по степеням x до x5 включительно. Представим функцию в виде
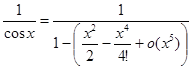 =1+u+u2+u3+o (u3), где u =
=1+u+u2+u3+o (u3), где u = 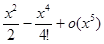 .
.
Тогда
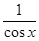 =1+u+u2+u3+o (u3) =1+
=1+u+u2+u3+o (u3) =1+ 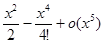 +
+ 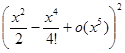 +
+ 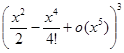 +
+ 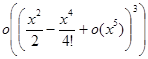 .
.
При вычислении степеней
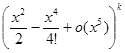
нас интересуют только слагаемые степеней не выше x5, более высокие степени войдут в o (x5). Таким образом,
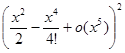 =
= 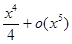 ,
, 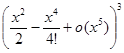 =
= 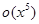 ,
, 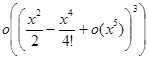 =
= 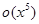 .
.
Выражение
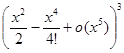 =
= 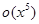
показывает, что в разложении
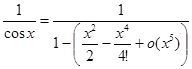 =1+u+u2+u3+o (u3)
=1+u+u2+u3+o (u3)
можно, с самого начала, ограничится второй степенью
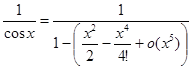 =1+u+u2+o (x5).
=1+u+u2+o (x5).
Подставляя нужные выражения в это равенство получим
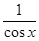 =1+
=1+ 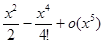 +
+ 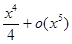 +
+ 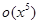 =1+
=1+ 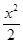 +
+ 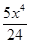 +
+ 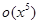 .
.
Пример 5. Используя разложение из предыдущего примера, разложить функцию f (x) =tg x по формуле Тейлора с остатком Пиано по степеням x до x6 включительно.
tg x= 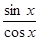 =
=
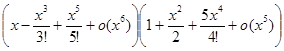 =
=
x+x2 (0) +x3 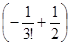 +x4 (0) +x5
+x4 (0) +x5 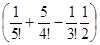 +x6 (0) =
+x6 (0) =
= 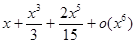
Пример 6. Разложить функцию f (x) = (1+x) a - (1 - x) a по формуле Тейлора с остатком Пиано.
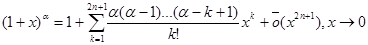
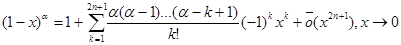
k = 2l+1, 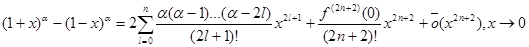
Таким образом,
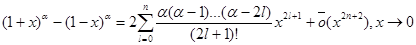
Следствие. 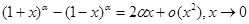
Пример 7. Используя следствие из предыдущего примера, найти предел (1401)
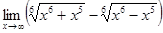 .
.
Имеем:
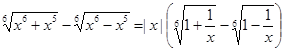 =|x|
=|x| 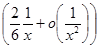 =
= 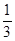 sign x +o (
sign x +o ( 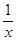 ).
).
Пример 8. Разложить функцию
f (x) = 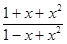
по формуле Тейлора с остатком Пиано по степеням x до x4 включительно.
Сначала выпишем разложение функции 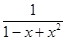 по степеням x до x3 включительно.
по степеням x до x3 включительно.
Положим u=x - x2, тогда
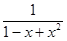 =
= 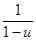 =1+ u+ u2+ u3+ o ( u3) =1+ x - x2+ ( x - x2) 2+ ( x - x2) 3+ o ( x3) =1+ x - x3 + o ( x3).
=1+ u+ u2+ u3+ o ( u3) =1+ x - x2+ ( x - x2) 2+ ( x - x2) 3+ o ( x3) =1+ x - x3 + o ( x3).
Далее,
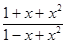 =
= 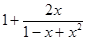 =1+2 x (1+ x - x3 + o ( x3)) =1+2 x+2 x2-2 x4+ o ( x4).
=1+2 x (1+ x - x3 + o ( x3)) =1+2 x+2 x2-2 x4+ o ( x4).
Второй способ. Так как
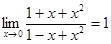 ,
,
то на первом шаге выделяем единицу:
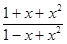 =
= 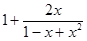 .
.
Второе слагаемое представляем в виде Cxng2 (x) так, чтобы 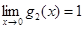 , после чего следует представить функцию g2 (x) в виде g2 (x) = 1+g3 (x) и т.д. В нашем случае:
, после чего следует представить функцию g2 (x) в виде g2 (x) = 1+g3 (x) и т.д. В нашем случае:
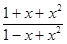 =
= 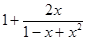 =
= 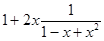 =
= 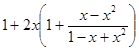 =
=
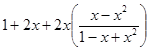 =
= 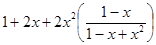 =1+2x+
=1+2x+ 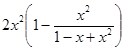 =
=
1+2x+2x2 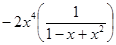 =1+2x+2x2-2x4+o (x4).
=1+2x+2x2-2x4+o (x4).
Дата: 2019-04-23, просмотров: 306.